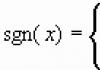Tele2 bo'yicha yordam, tariflar, savollar

Bugun, do'stlar, hech qanday og'riq va hissiyot bo'lmaydi. Buning o'rniga men sizni 8-9-sinf algebra kursidagi eng dahshatli raqiblardan biri bilan boshqa savollarsiz jangga yuboraman.

Ha, siz hamma narsani to'g'ri tushundingiz: biz modulli tengsizliklar haqida gapiramiz. Biz to'rtta asosiy texnikani ko'rib chiqamiz, ular yordamida siz ushbu muammolarning 90% ni hal qilishni o'rganasiz. Qolgan 10% haqida nima deyish mumkin? Xo'sh, biz ular haqida alohida darsda gaplashamiz. :)

Biroq, u erda biron bir hiyla-nayrangni tahlil qilishdan oldin, siz allaqachon bilishingiz kerak bo'lgan ikkita faktni eslamoqchiman. Aks holda, bugungi dars materialini umuman tushunmaslik xavfi bor.

Siz allaqachon bilishingiz kerak bo'lgan narsa

Kapitan dalillari, tengsizliklarni modul bilan hal qilish uchun siz ikkita narsani bilishingiz kerakligini ta'kidlaydi:

1. Tengsizliklar qanday hal qilinadi?
2. Modul nima.

Ikkinchi nuqtadan boshlaylik.

Modul ta'rifi

Bu erda hamma narsa oddiy. Ikkita ta'rif mavjud: algebraik va grafik. Keling, algebradan boshlaylik:

Ta'rif. $x$ sonining moduli, agar manfiy bo'lmasa, sonning o'zi yoki agar asl $x$ hali ham manfiy bo'lsa, unga qarama-qarshi bo'lgan sondir.

Bu shunday yozilgan:

\[\chap| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \o'ng.\]

Oddiy so'zlar bilan aytganda, modul "minussiz raqam" dir. Va bu ikkitomonlama (qaerdadir asl raqam bilan hech narsa qilishning hojati yo'q, lekin biron bir joyda u erda minuslarni olib tashlash kerak) va yangi boshlanuvchilar uchun barcha qiyinchiliklar yotadi.

Geometrik ta'rif ham mavjud. Buni bilish ham foydalidir, lekin biz unga faqat murakkab va ba'zi maxsus holatlarda murojaat qilamiz, bu erda geometrik yondashuv algebraikdan ko'ra qulayroqdir (spoiler: bugungi kunda emas).

Ta'rif. Haqiqiy chiziqda $a$ nuqta belgilansin. Keyin modul $\left| x-a \right|$ - bu chiziqdagi $x$ nuqtadan $a$ nuqtagacha bo'lgan masofa.

Agar siz rasm chizsangiz, siz shunga o'xshash narsani olasiz:

Grafik modul ta'rifi

Qanday bo'lmasin, uning asosiy xususiyati modul ta'rifidan darhol kelib chiqadi: sonning moduli har doim manfiy bo'lmagan qiymatdir. Bu haqiqat bugungi butun hikoyamiz bo'ylab qizil ip bo'ladi.

Tengsizliklarni yechish. Bo'shliq usuli

Endi tengsizliklar bilan shug'ullanamiz. Ularning ko'pi bor, ammo bizning vazifamiz hech bo'lmaganda ulardan eng oddiyini hal qilishdir. Chiziqli tengsizliklarga, shuningdek intervallar usuliga qisqartirilganlar.

Menda ushbu mavzu bo'yicha ikkita katta darslik bor (Aytgancha, juda, JUDA foydali - o'qishni tavsiya qilaman):

1. Tengsizliklar uchun interval usuli (ayniqsa, videoni tomosha qiling);
2. Kasr-ratsional tengsizliklar juda katta hajmli dars, ammo undan keyin sizda umuman savol qolmaydi.

Agar siz bularning barchasini bilsangiz, agar "tengsizlikdan tenglamaga o'taylik" iborasi sizni devorga qarshi o'ldirishni xohlamasa, unda siz tayyorsiz: darsning asosiy mavzusiga do'zaxga xush kelibsiz. :)

1. “Funksiyadan kichik modul” shaklidagi tengsizliklar.

Bu modullar bilan eng ko'p uchraydigan vazifalardan biridir. Shaklning tengsizligini yechish uchun talab qilinadi:

\[\chap| f\o'ng| \ltg\]

Har qanday narsa $f$ va $g$ funktsiyalari sifatida harakat qilishi mumkin, lekin odatda ular polinomlardir. Bunday tengsizliklarga misollar:

\[\begin(align) & \left| 2x+3\o'ng| \ltx+7; \\ & \chap| ((x)^(2))+2x-3 \o'ng|+3\chap(x+1 \o'ng) \lt 0; \\ & \chap| ((x)^(2))-2\chap| x \right|-3 \right| \lt 2. \\\end(tuzalash)\]

Ularning barchasi sxema bo'yicha tom ma'noda bitta qatorda hal qilinadi:

\[\chap| f\o'ng| \lt g\O'ng strelka -g \lt f \lt g\to'rt \chap (\O'ng strelka \chap\( \boshlang(hizalang) & f \lt g, \\ & f \gt -g \\\end(tekislang) \o'ng.\o'ng)\]

Ko'rish oson, biz moduldan xalos bo'lamiz, lekin buning o'rniga biz qo'sh tengsizlikni olamiz (yoki bir xil narsa, ikkita tengsizliklar tizimi). Ammo bu o'tish mutlaqo barcha mumkin bo'lgan muammolarni hisobga oladi: agar modul ostidagi raqam ijobiy bo'lsa, usul ishlaydi; salbiy bo'lsa, u hali ham ishlaydi; va $f$ yoki $g$ oʻrniga eng noadekvat funksiya bilan ham usul ishlaydi.

Tabiiyki, savol tug'iladi: bu osonroq emasmi? Afsuski, qila olmaysiz. Bu modulning butun nuqtasi.

Lekin falsafiylik yetarli. Keling, bir nechta muammolarni hal qilaylik:

Vazifa. Tengsizlikni yeching:

\[\chap| 2x+3\o'ng| \ltx+7\]

Qaror. Shunday qilib, bizda "modul kamroq" shaklidagi klassik tengsizlik mavjud - hatto o'zgartirish uchun hech narsa yo'q. Biz algoritmga muvofiq ishlaymiz:

\[\begin(align) & \left| f\o'ng| \lt g\O'ng strelka -g \lt f \lt g; \\ & \chap| 2x+3\o'ng| \lt x+7\O'ng strelka -\chap(x+7 \o'ng) \lt 2x+3 \lt x+7 \\\end(hizalang)\]

Oldinda "minus" qo'yilgan qavslarni ochishga shoshilmang: shoshqaloqlik tufayli siz haqoratli xatoga yo'l qo'yishingiz mumkin.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(hizalang) \o'ng.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \o'ngga.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \o'ng.\]

Muammo ikkita elementar tengsizlikka qisqartirildi. Biz ularning yechimlarini parallel real chiziqlarda qayd etamiz:

Ko'pchilikning kesishishi

Bu to'plamlarning kesishishi javob bo'ladi.

Javob: $x\in \left(-\frac(10)(3);4 \right)$

Vazifa. Tengsizlikni yeching:

\[\chap| ((x)^(2))+2x-3 \o'ng|+3\chap(x+1 \o'ng) \lt 0\]

Qaror. Bu vazifa biroz qiyinroq. Boshlash uchun biz ikkinchi atamani o'ngga siljitish orqali modulni ajratamiz:

\[\chap| ((x)^(2))+2x-3 \o'ng| \lt -3\chap(x+1 \o'ng)\]

Shubhasiz, bizda yana "modul kamroq" shaklidagi tengsizlik mavjud, shuning uchun biz allaqachon ma'lum bo'lgan algoritmga muvofiq moduldan xalos bo'lamiz:

\[-\left(-3\left(x+1 \o'ng) \o'ng) \lt ((x)^(2))+2x-3 \lt -3\chap(x+1 \o'ng)\]

Endi e'tibor bering: kimdir meni bu qavslar bilan bir oz buzuqman, deb aytadi. Lekin yana bir bor eslatib o'tamanki, bizning asosiy maqsadimiz tengsizlikni to‘g‘ri yeching va javobini oling. Keyinchalik, ushbu darsda tasvirlangan hamma narsani mukammal o'zlashtirganingizdan so'ng, siz o'zingizni xohlaganingizcha buzishingiz mumkin: qavslarni oching, minuslarni qo'shing va hokazo.

Yangi boshlanuvchilar uchun biz chap tomondagi ikki tomonlama minusdan xalos bo'lamiz:

\[-\left(-3\left(x+1 \o'ng) \o'ng)=\left(-1 \o'ng)\cdot \left(-3 \o'ng)\cdot \left(x+1 \o'ng) =3\chap(x+1\o'ng)\]

Endi juft tengsizlikdagi barcha qavslarni ochamiz:

Keling, ikki barobar tengsizlikka o'tamiz. Bu safar hisob-kitoblar jiddiyroq bo'ladi:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(tekislash) \o'ngga.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( tekislang)\o'ng.\]

Ikkala tengsizlik ham kvadrat bo'lib, interval usuli bilan yechiladi (shuning uchun aytaman: agar bu nima ekanligini bilmasangiz, modullarni hali qabul qilmaganingiz ma'qul). Birinchi tengsizlikdagi tenglamaga o'tamiz:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \o'ng)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(tekislash)\]

Ko'rib turganingizdek, chiqish elementar tarzda echiladigan to'liq bo'lmagan kvadrat tenglama bo'lib chiqdi. Endi tizimning ikkinchi tengsizligi bilan shug'ullanamiz. U erda siz Viet teoremasini qo'llashingiz kerak:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \o'ng)\left(x+2 \o'ng)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(tekislash)\]

Olingan raqamlarni ikkita parallel chiziqda belgilaymiz (birinchi tengsizlik uchun alohida, ikkinchisi uchun alohida):

Shunga qaramay, biz tengsizliklar tizimini yechayotganimiz sababli, bizni soyali to'plamlarning kesishishi qiziqtiradi: $x\in \left(-5;-2 \right)$. Bu javob.

Javob: $x\in \left(-5;-2 \right)$

Menimcha, ushbu misollardan keyin yechim sxemasi juda aniq:

1. Boshqa barcha shartlarni tengsizlikning qarama-qarshi tomoniga o'tkazish orqali modulni ajratib oling. Shunday qilib, biz $\left| ko'rinishdagi tengsizlikka erishamiz f\o'ng| \ltg$.
2. Yuqorida aytib o'tilganidek, moduldan qutulish orqali ushbu tengsizlikni hal qiling. Bir nuqtada, qo'shaloq tengsizlikdan ikkita mustaqil ifoda tizimiga o'tish kerak bo'ladi, ularning har biri allaqachon alohida yechilishi mumkin.
3. Nihoyat, ushbu ikkita mustaqil iboraning echimlarini kesib o'tish kifoya - va tamom, biz yakuniy javobni olamiz.

Modul funktsiyadan katta bo'lsa, xuddi shunday algoritm quyidagi turdagi tengsizliklar uchun mavjud. Biroq, bir nechta jiddiy "lekin" bor. Biz hozir bu "lekin" haqida gaplashamiz.

2. “Modul funksiyadan katta” ko’rinishdagi tengsizliklar.

Ular shunday ko'rinadi:

\[\chap| f\o'ng| \gt g\]

Avvalgisiga o'xshashmi? Dek tuyulyapti. Shunga qaramay, bunday vazifalar butunlay boshqacha tarzda hal qilinadi. Rasmiy ravishda, sxema quyidagicha:

\[\chap| f\o'ng| \gt g\O'ng strelka \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(hizalang) \o'ng.\]

Boshqacha qilib aytganda, biz ikkita holatni ko'rib chiqamiz:

1. Birinchidan, biz modulni shunchaki e'tiborsiz qoldiramiz - biz odatdagi tengsizlikni hal qilamiz;
2. Keyin, aslida, biz modulni minus belgisi bilan ochamiz, keyin esa tengsizlikning ikkala qismini ishora bilan -1 ga ko'paytiramiz.

Bunday holda, variantlar kvadrat qavs bilan birlashtiriladi, ya'ni. Bizda ikkita talabning kombinatsiyasi mavjud.

Yana bir bor e'tibor bering: bizning oldimizda tizim emas, balki yig'indi, shuning uchun javobda to'plamlar kesishmaydi, birlashtiriladi. Bu avvalgi paragrafdan tubdan farq qiladi!

Umuman olganda, ko'plab talabalar kasaba uyushmalari va chorrahalar bilan juda ko'p chalkashliklarga ega, shuning uchun keling, bu masalani bir marta va butunlay ko'rib chiqaylik:

• "∪" - birikma belgisi. Aslida, bu bizga ingliz tilidan kelgan va "Union" ning qisqartmasi bo'lgan stilize qilingan "U" harfi, ya'ni. "Assotsiatsiyalar".
• "∩" - kesishish belgisi. Bu axmoq hech qayerdan kelib chiqmagan, faqat "∪" ga muxolifat sifatida paydo bo'lgan.

Eslab qolish osonroq bo'lishi uchun ko'zoynak yasash uchun ushbu belgilarga oyoq qo'shing (shunchaki hozir meni giyohvandlik va alkogolizmni targ'ib qilishda ayblamang: agar siz ushbu darsni jiddiy o'rganayotgan bo'lsangiz, demak siz allaqachon giyohvandsiz):

To'plamlarning kesishishi va birlashuvi o'rtasidagi farq

Rus tiliga tarjima qilinganda, bu quyidagilarni anglatadi: birlashma (to'plam) ikkala to'plamning elementlarini o'z ichiga oladi, shuning uchun ularning har biridan kam emas; lekin kesishma (tizim) faqat birinchi to'plamda ham, ikkinchisida ham bo'lgan elementlarni o'z ichiga oladi. Shuning uchun to'plamlarning kesishishi hech qachon manba to'plamlaridan katta bo'lmaydi.

Shunday qilib, aniqroq bo'ldimi? Bu ajoyib. Keling, amaliyotga o'tamiz.

Vazifa. Tengsizlikni yeching:

\[\chap| 3x+1 \o'ng| \gt 5-4x\]

Qaror. Biz sxema bo'yicha harakat qilamiz:

\[\chap| 3x+1 \o'ng| \gt 5-4x\O'ng strelka \chap[ \begin(hizala) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \o'ng) \\\end(hizalang) \ to'g'ri.\]

Har bir aholi tengsizligini hal qilamiz:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(hizalang) \o'ngga.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \o'ng.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(hizala) \o'ng.\]

Biz har bir natija to'plamini raqamlar qatorida belgilaymiz va keyin ularni birlashtiramiz:

To'plamlar ittifoqi

Shubhasiz javob $x\in \left(\frac(4)(7);+\infty \right)$

Javob: $x\in \left(\frac(4)(7);+\infty \right)$

Vazifa. Tengsizlikni yeching:

\[\chap| ((x)^(2))+2x-3 \o'ng| \gtx\]

Qaror. Nima bopti? Yo'q, hammasi bir xil. Biz modulli tengsizlikdan ikkita tengsizliklar to'plamiga o'tamiz:

\[\chap| ((x)^(2))+2x-3 \o'ng| \gt x\O'ng strelka \left[ \begin(hizala) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\oxirgi (tekislash) \o'ngga.\]

Har bir tengsizlikni hal qilamiz. Afsuski, u erda ildizlar unchalik yaxshi bo'lmaydi:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(tekislash)\]

Ikkinchi tengsizlikda ham bir oz o'yin bor:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(tekislash)\]

Endi biz bu raqamlarni ikkita o'qda belgilashimiz kerak - har bir tengsizlik uchun bitta o'q. Biroq, siz nuqtalarni to'g'ri tartibda belgilashingiz kerak: raqam qanchalik katta bo'lsa, nuqta o'ngga siljiydi.

Va bu erda biz sozlashni kutmoqdamiz. Agar $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ raqamlari bilan hamma narsa aniq bo'lsa (birinchi raqamdagi shartlar) kasr sekundning numeratoridagi hadlardan kichik, shuning uchun yig'indi ham kichikroq bo'lib, $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt) raqamlari bilan (21))(2)$ ham hech qanday qiyinchilik bo'lmaydi (musbat raqam aniqroq salbiy), lekin oxirgi juftlik bilan hamma narsa unchalik oddiy emas. Qaysi biri kattaroq: $\frac(-3+\sqrt(21))(2)$ yoki $\frac(-1+\sqrt(13))(2)$? Raqamli chiziqlardagi nuqtalarning joylashishi va aslida javob bu savolga javobga bog'liq bo'ladi.

Shunday qilib, keling, taqqoslaylik:

\[\begin(matritsa) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matritsa)\]

Biz ildizni ajratib oldik, tengsizlikning ikkala tomonida manfiy bo'lmagan raqamlarni oldik, shuning uchun biz ikkala tomonni kvadratga solish huquqiga egamiz:

\[\begin(matritsa) ((\left(2+\sqrt(13) \o'ng))^(2))\vee ((\left(\sqrt(21) \o'ng))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matritsa)\]

Menimcha, $4\sqrt(13) \gt 3$, shuning uchun $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, nihoyat, o'qlardagi nuqtalar quyidagicha tartibga solinadi:

Xunuk ildizlar holati

Sizga eslatib o'tamanki, biz to'plamni hal qilyapmiz, shuning uchun javob soyali to'plamlarning kesishmasi emas, balki birlashma bo'ladi.

Javob: $x\in \left(-\infty;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2) );+\infty\right)$

Ko'rib turganingizdek, bizning sxemamiz oddiy vazifalar uchun ham, juda qiyin bo'lganlar uchun ham ajoyib ishlaydi. Ushbu yondashuvdagi yagona "zaif nuqta" shundaki, siz irratsional sonlarni to'g'ri taqqoslashingiz kerak (va menga ishoning: bu nafaqat ildizlar). Ammo taqqoslash savollariga alohida (va juda jiddiy dars) bag'ishlanadi. Va biz davom etamiz.

3. Manfiy bo'lmagan "dumlar" bilan tengsizliklar

Shunday qilib, biz eng qiziqarlisiga keldik. Bu shakldagi tengsizliklar:

\[\chap| f\o'ng| \gt\left| g\o'ng|\]

Umuman olganda, biz hozir gaplashadigan algoritm faqat modul uchun to'g'ri keladi. U chap va o'ngda kafolatlangan salbiy bo'lmagan ifodalar mavjud bo'lgan barcha tengsizliklarda ishlaydi:

Bu vazifalar bilan nima qilish kerak? Faqat esda tuting:

Salbiy bo'lmagan quyruqli tengsizliklarda ikkala tomon ham har qanday tabiiy kuchga ko'tarilishi mumkin. Hech qanday qo'shimcha cheklovlar bo'lmaydi.

Avvalo, biz kvadratlashtirishga qiziqamiz - u modullar va ildizlarni yoqib yuboradi:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\ chap (\ sqrt (f) \ o'ng)) ^ (2)) = f. \\\end(tekislash)\]

Buni kvadratning ildizini olish bilan adashtirmang:

\[\sqrt(((f)^(2)))=\chap| f \right|\ne f\]

Talaba modul o'rnatishni unutganida son-sanoqsiz xatolarga yo'l qo'yildi! Ammo bu butunlay boshqacha hikoya (bular, go'yo irratsional tenglamalar), shuning uchun biz hozir unga kirmaymiz. Keling, bir nechta muammolarni yaxshiroq hal qilaylik:

Vazifa. Tengsizlikni yeching:

\[\chap| x+2 \right|\ge \left| 1-2x \o'ng|\]

Qaror. Biz darhol ikkita narsani sezamiz:

1. Bu qat'iy bo'lmagan tengsizlik. Raqam chizig'idagi nuqtalar punch bilan chiqariladi.
2. Tengsizlikning ikkala tomoni ham manfiy emas (bu modulning xususiyati: $\left| f\left(x \right) \right|\ge 0$).

Shunday qilib, moduldan xalos bo'lish va muammoni odatiy interval usuli yordamida hal qilish uchun biz tengsizlikning ikkala tomonini kvadratga olamiz:

\[\begin(hizala) & ((\left(\left| x+2 \o'ng| \o'ng))^(2))\ge ((\left(\left| 1-2x \o'ng| \o'ng)) )^(2)); \\ & ((\left(x+2 \o'ng))^(2))\ge ((\left(2x-1 \o'ng))^(2)). \\\end (tekislash)\]

Oxirgi bosqichda men biroz aldadim: modul paritetidan foydalanib, atamalar ketma-ketligini o'zgartirdim (aslida $1-2x$ ifodasini -1 ga ko'paytirdim).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \o'ng)-\left(x+2 \o'ng) \o'ng)\cdot \left(\left(2x-1 \o'ng)+\chap(x+2 \ o'ng)\o'ng)\le 0; \\ & \left(2x-1-x-2 \o'ng)\cdot \left(2x-1+x+2 \o'ng)\le 0; \\ & \left(x-3 \o'ng)\cdot \left(3x+1 \o'ng)\le 0. \\\end(align)\]

Interval usuli bilan hal qilamiz. Tengsizlikdan tenglamaga o'tamiz:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end (tekislash)\]

Topilgan ildizlarni raqamlar qatorida belgilaymiz. Yana bir bor: barcha nuqtalar soyali, chunki asl tengsizlik qat'iy emas!

Modul belgisidan qutulish

Ayniqsa, o'jarlar uchun eslatib o'taman: biz tenglamaga o'tishdan oldin yozilgan oxirgi tengsizlikdan belgilarni olamiz. Va biz bir xil tengsizlikda talab qilinadigan maydonlarni bo'yab qo'yamiz. Bizning holatda, bu $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Bo'ldi shu. Muammo hal qilindi.

Javob: $x\in \left[ -\frac(1)(3);3 \right]$.

Vazifa. Tengsizlikni yeching:

\[\chap| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \o'ng|\]

Qaror. Biz hamma narsani xuddi shunday qilamiz. Men izoh bermayman - faqat harakatlar ketma-ketligiga qarang.

Keling, uni kvadratga aylantiramiz:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \o'ng| \o'ng))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \o'ng| \o'ng))^(2)); \\ & ((\left(((x)^(2))+x+1 \o'ng))^(2))\le ((\left(((x)^(2))+3x+4 \right)))^(2)); \\ & ((\left(((x)^(2))+x+1 \o'ng))^(2))-((\left(((x)^(2))+3x+4 \ o'ng))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x)) ^(2))+x+1+((x)^(2))+3x+4 \o‘ng)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \o'ng)\le 0. \\\end(align)\]

Bo'shliq usuli:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \o'ng)=0 \\ & -2x-3=0\ O'ng strelka x=-1,5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varnothing . \\\end(tekislash)\]

Raqamlar qatorida faqat bitta ildiz bor:

Javob to'liq diapazondir

Javob: $x\in \left[ -1.5;+\infty \right)$.

Oxirgi vazifa haqida kichik eslatma. Mening talabalarimdan biri aniq ta'kidlaganidek, ushbu tengsizlikdagi ikkala submodul iborasi ham ijobiy, shuning uchun modul belgisi sog'likka zarar bermasdan qoldirilishi mumkin.

Ammo bu allaqachon butunlay boshqacha fikrlash darajasi va boshqa yondashuv - uni shartli ravishda oqibatlar usuli deb atash mumkin. U haqida - alohida darsda. Va endi bugungi darsning yakuniy qismiga o'tamiz va har doim ishlaydigan universal algoritmni ko'rib chiqamiz. Oldingi barcha yondashuvlar kuchsiz bo'lsa ham. :)

4. Variantlarni sanab o'tish usuli

Agar bu hiyla-nayranglarning barchasi ishlamasa-chi? Agar tengsizlik salbiy bo'lmagan dumlargacha kamaymasa, modulni izolyatsiya qilishning iloji bo'lmasa, agar umuman og'riq-qayg'u-hasrat bo'lsa?

Keyin sahnaga barcha matematikaning "og'ir artilleriyasi" kiradi - ro'yxatga olish usuli. Modul bilan tengsizliklarga kelsak, u quyidagicha ko'rinadi:

1. Barcha submodul ifodalarini yozing va ularni nolga tenglang;
2. Olingan tenglamalarni yeching va topilgan ildizlarni bitta son qatoriga belgilang;
3. To'g'ri chiziq bir nechta bo'limlarga bo'linadi, ularning ichida har bir modul o'zgarmas belgiga ega va shuning uchun bir ma'noda kengayadi;
4. Har bir bunday bo'lim bo'yicha tengsizlikni yeching (siz 2-bandda olingan chegara ildizlarini alohida ko'rib chiqishingiz mumkin - ishonchlilik uchun). Natijalarni birlashtiring - bu javob bo'ladi. :)

Qanday? Zaifmi? Oson! Faqat uzoq vaqt. Keling, amalda ko'rib chiqaylik:

Vazifa. Tengsizlikni yeching:

\[\chap| x+2 \o'ng| \lt\chap| x-1 \o'ng|+x-\frac(3)(2)\]

Qaror. Bu ahmoqlik $\left| kabi tengsizliklarga tushmaydi f\o'ng| \lt g$, $\chap| f\o'ng| \gt g$ yoki $\left| f\o'ng| \lt\chap| g \right|$, keling, davom etaylik.

Biz submodul ifodalarini yozamiz, ularni nolga tenglashtiramiz va ildizlarni topamiz:

\[\boshlang(align) & x+2=0\O'ng strelka x=-2; \\ & x-1=0\Oʻng strelka x=1. \\\end(tekislash)\]

Hammasi bo'lib, bizda raqamlar chizig'ini uchta bo'limga ajratadigan ikkita ildiz bor, ularning ichida har bir modul o'ziga xos tarzda ochiladi:

Submodulyar funksiyalarning son qatorini nolga bo'lish

Keling, har bir bo'limni alohida ko'rib chiqaylik.

1. $x \lt -2$ bo'lsin. Keyin ikkala submodul ifodasi manfiy bo'lib, asl tengsizlik quyidagicha qayta yoziladi:

\[\begin(hizala) & -\left(x+2 \o'ng) \lt -\left(x-1 \o'ng)+x-1,5 \\ & -x-2 \lt -x+1+ x-1,5 \\ & x \gt 1,5 \\\end(tuzalash)\]

Bizda juda oddiy cheklov bor. Keling, uni $x \lt -2$ degan dastlabki taxmin bilan kesib olaylik:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Shubhasiz, $x$ o'zgaruvchisi bir vaqtning o'zida -2 dan kichik bo'lishi mumkin emas, lekin 1,5 dan katta bo'lishi mumkin emas. Bu sohada hech qanday yechim yo'q.

1.1. Chegaraviy holatni alohida ko'rib chiqamiz: $x=-2$. Keling, bu raqamni asl tengsizlikka almashtiramiz va tekshiramiz: u mos keladimi?

\[\begin(hizala) & ((\chap. \chap| x+2 \o'ng| \lt \chap| x-1 \o'ng|+x-1,5 \o'ng|)_(x=-2) ) \\ & 0 \lt \chap| -3 \right|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\O'ng ko'rsatkich \varnothing . \\\end(tekislash)\]

Shubhasiz, hisob-kitoblar zanjiri bizni noto'g'ri tengsizlikka olib keldi. Demak, asl tengsizlik ham noto'g'ri va $x=-2$ javobga kiritilmagan.

2. Endi $-2 \lt x \lt 1$ bo'lsin. Chap modul allaqachon "ortiqcha" bilan ochiladi, lekin o'ng modul hali ham "minus" bilan. Bizda ... bor:

\[\boshlang(tuzala) & x+2 \lt -\chap(x-1 \o'ng)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2.5 \\\end (tekislash)\]

Biz yana asl talab bilan kesishamiz:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \o'ng.\O'ng strelka x\in \varnothing \]

Va yana, bo'sh echimlar to'plami, chunki -2,5 dan kichik va -2 dan katta raqamlar yo'q.

2.1. Va yana bir alohida holat: $x=1$. Biz asl tengsizlikni almashtiramiz:

\[\begin(hizala) & ((\chap. \chap| x+2 \o'ng| \lt \chap| x-1 \o'ng|+x-1,5 \o'ng|)_(x=1)) \\ & \chap| 3\o'ng| \lt\chap| 0 \right|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\O'ng ko'rsatkich \varnothing . \\\end(tekislash)\]

Oldingi "maxsus holat"ga o'xshab, javobda $x=1$ raqami aniq kiritilmagan.

3. Qatorning oxirgi qismi: $x \gt 1$. Bu erda barcha modullar ortiqcha belgisi bilan kengaytirilgan:

\[\boshlang(align) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(hizalang)\ ]

Va yana topilgan to'plamni asl cheklov bilan kesib o'tamiz:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\O'ng strelka x\ichida \chap(4,5;+\infty) \o'ng)\]

Va nihoyat! Biz javob bo'ladigan intervalni topdik.

Javob: $x\in \left(4,5;+\infty \right)$

Va nihoyat, haqiqiy muammolarni hal qilishda sizni ahmoqona xatolardan qutqarishi mumkin bo'lgan bir eslatma:

Modullar bilan tengsizliklarning yechimlari odatda raqamlar chizig'idagi uzluksiz to'plamlar - intervallar va segmentlardir. Izolyatsiya qilingan nuqtalar juda kam uchraydi. Va undan ham kamdan-kam hollarda, yechimning chegaralari (segmentning oxiri) ko'rib chiqilayotgan diapazonning chegarasiga to'g'ri keladi.

Shuning uchun, agar chegaralar (o'sha "maxsus holatlar") javobga kiritilmagan bo'lsa, unda bu chegaralarning chap-o'ng tomonidagi joylar ham javobga deyarli kiritilmaydi. Va aksincha: chegara javob sifatida kirdi, demak, uning atrofidagi ba'zi hududlar ham javoblar bo'ladi.

Yechimlaringizni tekshirganda buni yodda saqlang.

Va bugungi kunda hamma ham ratsional tengsizliklarni hal qila olmaydi. Aniqrog'i, faqat hamma ham qaror qila olmaydi. Buni kam odam qila oladi.
Klichko

Bu dars qiyin bo'ladi. Shu qadar qiyinki, faqat tanlanganlar buning oxiriga etadi. Shuning uchun, o'qishdan oldin, men ayollarni, mushuklarni, homilador bolalarni va ...

OK, aslida bu juda oddiy. Faraz qiling, siz intervalli metodni o‘zlashtirgansiz (agar o‘zlashtirmagan bo‘lsangiz, orqaga qaytib, o‘qishni tavsiya qilaman) va $P\left(x \right) \gt 0$ ko‘rinishidagi tengsizliklarni yechish yo‘llarini o‘rgandingiz, bu yerda $P. \left(x \right)$ — baʼzi koʻphad yoki koʻphadlarning koʻpaytmasi.

Ishonamanki, masalan, bunday o'yinni hal qilish siz uchun qiyin bo'lmaydi (aytmoqchi, uni isinish uchun sinab ko'ring):

\[\begin(align) & \left(2((x)^(2))+3x+4 \right)\left(4x+25 \right) \gt 0; \\ & x\left(2((x)^(2))-3x-20 \o'ng)\left(x-1 \o'ng)\ge 0; \\ & \left(8x-((x)^(4)) \o'ng)((\left(x-5 \o'ng))^(6))\le 0. \\ \end(align)\]

Endi vazifani biroz murakkablashtiramiz va nafaqat ko'phadlarni, balki shaklning ratsional kasrlarini ham ko'rib chiqamiz:

bu yerda $P\left(x \right)$ va $Q\left(x \right)$ $((a)_(n))((x)^(n))+( koʻrinishdagi bir xil polinomlardir. ( a)_(n-1))((x)^(n-1))+...+((a)_(0))$ yoki bunday koʻphadlarning koʻpaytmasi.

Bu ratsional tengsizlik bo'ladi. Asosiy nuqta - $x$ o'zgaruvchisining maxrajda mavjudligi. Masalan, ratsional tengsizliklar:

\[\begin(align) & \frac(x-3)(x+7) \lt 0; \\ & \frac(\left(7x+1 \o'ng)\left(11x+2 \o'ng))(13x-4)\ge 0; \\ & \frac(3((x)^(2))+10x+3)(((\left(3-x \o'ng))^(2))\left(4-((x)^( 2)) \o‘ng))\ge 0. \\ \end(align)\]

Va bu mantiqiy emas, balki intervalli usul bilan hal qilinadigan eng keng tarqalgan tengsizlik:

\[\frac(((x)^(2))+6x+9)(5)\ge 0\]

Oldinga qarab, men darhol aytaman: ratsional tengsizliklarni hal qilishning kamida ikkita usuli bor, ammo ularning barchasi u yoki bu tarzda bizga ma'lum bo'lgan intervallar usuliga qisqartirilgan. Shuning uchun, ushbu usullarni tahlil qilishdan oldin, keling, eski faktlarni eslaylik, aks holda yangi materialdan hech qanday ma'no bo'lmaydi.

Siz allaqachon bilishingiz kerak bo'lgan narsa

Ko'p muhim faktlar mavjud emas. Bizga faqat to'rtta kerak.

Qisqartirilgan ko'paytirish formulalari

Ha, ha: ular bizni maktab matematika o'quv dasturi davomida ta'qib qilishadi. Va universitetda ham. Ushbu formulalarning bir nechtasi bor, ammo bizga faqat quyidagilar kerak:

\[\begin(align) & ((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \o'ng))^(2)); \\ & ((a)^(2))-((b)^(2))=\left(a-b \o'ng)\left(a+b \o'ng); \\ & ((a)^(3))+(b)^(3))=\left(a+b \o'ng)\left(((a)^(2))-ab+((b) ^(2))\o'ng); \\ & ((a)^(3))-(b)^(3))=\left(a-b \o'ng)\left(((a)^(2))+ab+(b)^( 2))\o‘ng). \\ \end (tekislash)\]

Oxirgi ikkita formulaga e'tibor bering - bu kublarning yig'indisi va farqi (yig'indi yoki farqning kubi emas!). Agar birinchi qavsdagi belgi asl iboradagi belgi bilan bir xil, ikkinchi qavsdagi esa asl iboradagi belgiga qarama-qarshi ekanligini sezsangiz, ularni eslab qolish oson.

Chiziqli tenglamalar

Bular $ax+b=0$ koʻrinishidagi eng oddiy tenglamalar boʻlib, bunda $a$ va $b$ oddiy sonlar va $a\ne 0$. Bu tenglamani yechish oson:

\[\boshlang(hatlang) & ax+b=0; \\ &ax=-b; \\ & x=-\ frac(b)(a). \\ \end (tekislash)\]

Shuni ta'kidlaymanki, biz $a$ koeffitsientiga bo'lish huquqiga egamiz, chunki $a\ne 0$. Bu talab juda mantiqiy, chunki $a=0$ bilan biz buni olamiz:

Birinchidan, bu tenglamada $x$ o'zgaruvchisi yo'q. Bu, umuman olganda, bizni chalkashtirmasligi kerak (bu, masalan, geometriyada va juda tez-tez sodir bo'ladi), lekin biz endi chiziqli tenglama emasmiz.

Ikkinchidan, bu tenglamaning yechimi faqat $b$ koeffitsientiga bog'liq. Agar $b$ ham nolga teng bo'lsa, bizning tenglamamiz $0=0$ bo'ladi. Bu tenglik har doim to'g'ri; shuning uchun $x$ har qanday raqam (odatda \mathbb(R)$da $x\ shaklida yoziladi). Agar $b$ koeffitsienti nolga teng bo'lmasa, u holda $b=0$ tengligi hech qachon bajarilmaydi, ya'ni. javob yo'q ($x\da \varnothing $ deb yozilgan va "yechimlar to'plami bo'sh" deb o'qing).

Bu barcha murakkabliklarga yo'l qo'ymaslik uchun biz shunchaki $a\ne 0$ deb hisoblaymiz, bu esa bizni keyingi mulohazalarni hech qanday tarzda cheklamaydi.

Kvadrat tenglamalar

Sizga shuni eslatib o'tamanki, bu kvadrat tenglama deyiladi:

Bu erda chap tomonda ikkinchi darajali ko'phad va yana $a\ne 0$ (aks holda kvadrat tenglama o'rniga chiziqli tenglamani olamiz). Diskriminant yordamida quyidagi tenglamalar yechiladi:

1. Agar $D \gt 0$ bo'lsa, biz ikki xil ildiz olamiz;
2. Agar $D=0$ boʻlsa, unda ildiz bitta boʻladi, lekin ikkinchi koʻplikdan (u qanday koʻplik va uni qanday hisobga olish kerak - bu haqda keyinroq). Yoki tenglama ikkita bir xil ildizga ega deb aytishimiz mumkin;
3. $D \lt 0$ uchun hech qanday ildiz yoʻq va har qanday $x$ uchun $a((x)^(2))+bx+c$ koʻphadning belgisi $a koeffitsienti belgisi bilan mos keladi. $. Aytgancha, bu juda foydali fakt bo'lib, negadir algebra darslarida aytilishi unutilgan.

Ildizlarning o'zi taniqli formula bo'yicha hisoblanadi:

\[((x)_(1,2))=\frac(-b\pm \sqrt(D))(2a)\]

Aytgancha, diskriminantga nisbatan cheklovlar. Axir manfiy sonning kvadrat ildizi mavjud emas. Ildizlarga kelsak, ko'plab talabalarning boshlarida dahshatli tartibsizlik bor, shuning uchun men butun darsni maxsus yozib oldim: algebrada ildiz nima va uni qanday hisoblash mumkin - men uni o'qishni tavsiya qilaman. :)

Ratsional kasrlar bilan amallar

Yuqorida yozilganlarning barchasi, siz intervallar usulini o'rganganmisiz, allaqachon bilasiz. Ammo biz hozir tahlil qiladigan narsaning o'tmishda o'xshashi yo'q - bu mutlaqo yangi fakt.

Ta'rif. Ratsional kasr shaklning ifodasidir

\[\frac(P\left(x \o'ng))(Q\chap(x \o'ng))\]

bu yerda $P\left(x \right)$ va $Q\left(x \right)$ polinomlardir.

Ko'rinib turibdiki, bunday kasrdan tengsizlikni olish oson - o'ngga "kattaroq" yoki "kamroq" belgisini qo'yish kifoya. Va birozdan keyin biz bunday muammolarni hal qilish zavq ekanligini bilib olamiz, u erda hamma narsa juda oddiy.

Muammolar bir ifodada bir nechta shunday kasrlar mavjud bo'lganda boshlanadi. Ularni umumiy maxrajga qisqartirish kerak - va ayni paytda ko'plab hujumkor xatolarga yo'l qo'yilmoqda.

Shuning uchun ratsional tenglamalarni muvaffaqiyatli yechish uchun ikkita ko'nikmani mustahkam egallash kerak:

1. $P\left(x \right)$ koʻphadini koʻpaytmalarga ajratish;
2. Aslida, kasrlarni umumiy maxrajga keltirish.

Polinomni qanday qilib faktorlarga ajratish mumkin? Juda oddiy. Shaklning ko'phadiga ega bo'lsin

Keling, uni nolga tenglashtiramiz. Biz $n$-chi darajali tenglamani olamiz:

\[((a)_(n))((x)^(n))+((a)_(n-1))((x)^(n-1))+...+(( a)_(1))x+((a)_(0))=0\]

Aytaylik, biz bu tenglamani yechdik va $((x)_(1)),\ ...,\ ((x)_(n))$ ildizlarini oldik (xavotir olmang: ko‘p hollarda bunday bo‘lmaydi. bu ildizlarning ikkitadan ko'pi). Bunday holda, bizning asl polinomimiz quyidagicha qayta yozilishi mumkin:

\[\begin(align) & P\left(x \right)=((a)_(n))((x)^(n))+((a)_(n-1))((x) )^(n-1))+...+((a)_(1))x+((a)_(0))= \\ & =(a)_(n))\chap(x) -((x)_(1)) \o'ng)\cdot \left(x-((x)_(2)) \o'ng)\cdot ...\cdot \left(x-((x)_( n)) \o'ng) \end(tuzalash)\]

Ana xolos! E'tibor bering: $((a)_(n))$ yetakchi koeffitsienti hech qayerda yo'qolgan emas - bu qavslar oldida alohida omil bo'ladi va agar kerak bo'lsa, uni ushbu qavslarning istalganiga kiritish mumkin (amaliy ko'rsatuvlar). $((a)_ (n))\ne \pm 1$ bilan ildizlar orasida deyarli har doim kasrlar mavjud).

Vazifa. Ifodani soddalashtiring:

\[\frac(((x)^(2))+x-20)(x-4)-\frac(2((x)^(2))-5x+3)(2x-3)-\ frac(4-8x-5((x)^(2)(x+2)\]

Qaror. Birinchidan, maxrajlarni ko'rib chiqaylik: ularning barchasi chiziqli binomlar va bu erda faktorlarga ajratish uchun hech narsa yo'q. Shunday qilib, keling, sonlarni koeffitsientlarga ajratamiz:

\[\begin(align) & ((x)^(2))+x-20=\left(x+5 \right)\left(x-4 \right); \\ & 2((x)^(2))-5x+3=2\chap(x-\frac(3)(2) \o'ng)\left(x-1 \o'ng)=\chap(2x- 3\o'ng)\chap(x-1\o'ng); \\ & 4-8x-5((x)^(2))=-5\chap(x+2 \o'ng)\left(x-\frac(2)(5) \o'ng)=\chap(x +2 \o'ng)\chap (2-5x \o'ng). \\\end (tekislash)\]

E'tibor bering: ikkinchi polinomda "2" katta koeffitsienti bizning sxemamizga to'liq mos ravishda, avval qavs oldida paydo bo'ldi, keyin esa birinchi qavsga kiritildi, chunki u erda kasr chiqdi.

Xuddi shu narsa uchinchi ko'phadda sodir bo'ldi, faqat u erda atamalarning tartibi ham chalkashib ketgan. Biroq, "-5" koeffitsienti ikkinchi qavsga kiritilishi bilan yakunlandi (esda tuting: siz bitta va faqat bitta qavsga omil kiritishingiz mumkin!), Bu bizni kasr ildizlari bilan bog'liq noqulaylikdan qutqardi.

Birinchi polinomga kelsak, u erda hamma narsa oddiy: uning ildizlari standart usulda diskriminant orqali yoki Vieta teoremasi yordamida izlanadi.

Keling, asl iboraga qaytaylik va uni koeffitsientlarga ajratilgan sonlar bilan qayta yozamiz:

\[\begin(matritsa) \frac(\left(x+5 \o'ng)\left(x-4 \o'ng))(x-4)-\frac(\left(2x-3 \o'ng)\left( x-1 \o'ng))(2x-3)-\frac(\chap(x+2 \o'ng)\chap(2-5x \o'ng))(x+2)= \\ =\chap(x+5) \o'ng)-\left(x-1 \o'ng)-\chap(2-5x \o'ng)= \\ =x+5-x+1-2+5x= \\ =5x+4. \\ \end (matritsa)\]

Javob: $5x+4$.

Ko'rib turganingizdek, hech qanday murakkab narsa yo'q. Bir oz 7-8-sinf matematika va tamom. Barcha o'zgarishlarning maqsadi murakkab va qo'rqinchli ifodani oddiy va oson ishlashga aylantirishdir.

Biroq, bu har doim ham shunday bo'lmaydi. Shunday qilib, endi biz jiddiyroq muammoni ko'rib chiqamiz.

Lekin, avvalo, ikkita kasrni umumiy maxrajga qanday keltirish kerakligini aniqlaymiz. Algoritm juda oddiy:

1. Ikkala maxrajni ham faktorlarga ajrating;
2. Birinchi maxrajni ko'rib chiqing va unga ikkinchi maxrajda mavjud bo'lgan omillarni qo'shing, lekin birinchisida emas. Olingan mahsulot umumiy maxraj bo'ladi;
3. Asl kasrlarning har birida qanday omillar yetishmasligini aniqlang, shunda maxrajlar umumiy kasrga teng bo'ladi.

Ehtimol, bu algoritm sizga shunchaki "ko'p harflar" bo'lgan matn bo'lib tuyulishi mumkin. Shunday qilib, keling, aniq bir misolni ko'rib chiqaylik.

Vazifa. Ifodani soddalashtiring:

\[\left(\frac(x)((x)^(2))+2x+4)+\frac(((x)^(2))+8)((x)^(3) )-8)-\frac(1)(x-2) \o'ng)\cdot \left(\frac(((x)^(2))(((x)^(2))-4)- \frac(2)(2-x) \o'ng)\]

Qaror. Bunday katta hajmli vazifalar qismlarga bo'lib hal qilinadi. Keling, birinchi qavsda nima borligini yozamiz:

\[\frac(x)((x)^(2))+2x+4)+\frac(((x)^(2))+8)((x)^(3))-8 )-\frac(1)(x-2)\]

Oldingi muammodan farqli o'laroq, bu erda denominatorlar unchalik oddiy emas. Keling, ularning har birini faktorlarga ajratamiz.

$((x)^(2))+2x+4$ kvadrat trinomialni koeffitsientlarga ajratib bo‘lmaydi, chunki $((x)^(2))+2x+4=0$ tenglamaning ildizlari yo‘q (diskriminant manfiy) . Biz uni o'zgarishsiz qoldiramiz.

Ikkinchi maxraj, kubik polinom $((x)^(3))-8$, yaqinroq o'rganib chiqilsa, kublar farqidir va qisqartirilgan ko'paytirish formulalari yordamida osongina parchalanishi mumkin:

\[((x)^(3))-8=((x)^(3))-((2)^(3))=\left(x-2 \o'ng)\left(((x)) ^(2))+2x+4 \o'ng)\]

Boshqa hech narsani faktorlarga ajratib bo'lmaydi, chunki birinchi qavs chiziqli binomialni o'z ichiga oladi, ikkinchisida esa bizga allaqachon tanish bo'lgan, haqiqiy ildizga ega bo'lmagan konstruktsiya mavjud.

Nihoyat, uchinchi maxraj chiziqli binom bo'lib, uni parchalab bo'lmaydi. Shunday qilib, bizning tenglamamiz quyidagi shaklni oladi:

\[\frac(x)((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\left(x-2 \o'ng)\chap (((x)^(2))+2x+4 \o'ng))-\frac(1)(x-2)\]

Ko'rinib turibdiki, $\left(x-2 \right)\left((x)^(2))+2x+4 \right)$ umumiy maxraj bo'ladi va unga barcha kasrlarni kamaytirish uchun siz birinchi kasrni $\left(x-2 \right)$ ga, oxirgi qismini esa $\left(((x)^(2))+2x+4 \right)$ ga ko'paytirish kerak. Keyin faqat quyidagilarni keltirish qoladi:

\[\begin(matritsa) \frac(x\cdot \left(x-2 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \ o'ng))+\frac(((x)^(2))+8)(\left(x-2 \o'ng)\left(((x)^(2))+2x+4 \o'ng))- \frac(1\cdot \left(((x)^(2))+2x+4 \o'ng))(\left(x-2 \o'ng)\left(((x)^(2))+2x +4 \o'ng))= \\ =\frac(x\cdot \left(x-2 \o'ng)+\left(((x)^(2))+8 \o'ng)-\chap(((x) )^(2))+2x+4 \o'ng))(\left(x-2 \o'ng)\left(((x)^(2))+2x+4 \o'ng))= \\ =\frac (((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \o'ng)\chap (((x)^(2))+2x+4 \o'ng))= \\ =\frac(((x)^(2))-4x+4)(\left(x-2 \o'ng)\ chap (((x)^(2))+2x+4 \o'ng)). \\ \end (matritsa)\]

Ikkinchi qatorga e'tibor bering: denominator allaqachon keng tarqalgan bo'lsa, ya'ni. uchta alohida kasr o'rniga biz bitta katta qismini yozdik, siz darhol qavslardan xalos bo'lmasligingiz kerak. Qo'shimcha qator yozish va shuni ta'kidlash kerakki, aytaylik, uchinchi kasrdan oldin minus bor edi - va u hech qaerga ketmaydi, lekin qavs oldidagi hisoblagichga "osilib qoladi". Bu sizni ko'p xatolardan qutqaradi.

Xo'sh, oxirgi qatorda hisoblagichni faktorlarga ajratish foydalidir. Bundan tashqari, bu aniq kvadrat va qisqartirilgan ko'paytirish formulalari yana yordamimizga keladi. Bizda ... bor:

\[\frac(((x)^(2))-4x+4)(\left(x-2 \o'ng)\left(((x)^(2))+2x+4 \o'ng))= \frac(((\left(x-2 \o'ng))^(2)))(\left(x-2 \o'ng)\left(((x)^(2))+2x+4 \o'ng) )=\frac(x-2)((x)^(2))+2x+4)\]

Endi ikkinchi qavs bilan xuddi shu tarzda ishlaymiz. Bu erda men oddiygina tenglik zanjirini yozaman:

\[\begin(matritsa) \frac(((x)^(2)))(((x)^(2))-4)-\frac(2)(2-x)=\frac((( x)^(2))))(\left(x-2 \o'ng)\left(x+2 \o'ng))-\frac(2)(2-x)= \\ =\frac(((x)) ^(2)))(\left(x-2 \o'ng)\left(x+2 \o'ng))+\frac(2)(x-2)= \\ =\frac((x)^( 2)))(\left(x-2 \o'ng)\left(x+2 \o'ng))+\frac(2\cdot \left(x+2 \o'ng))(\left(x-2 \o'ng) )\cdot \left(x+2 \o'ng))= \\ =\frac(((x)^(2))+2\cdot \left(x+2 \o'ng))(\left(x-2) \o'ng)\left(x+2 \o'ng))=\frac(((x)^(2))+2x+4)(\left(x-2 \o'ng)\left(x+2 \o'ng) ). \\ \end (matritsa)\]

Biz asl muammoga qaytamiz va mahsulotga qaraymiz:

\[\frac(x-2)((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2) \o'ng)\left(x+2 \o'ng))=\frac(1)(x+2)\]

Javob: \[\frac(1)(x+2)\].

Ushbu muammoning ma'nosi avvalgisi bilan bir xil: agar siz ularni o'zgartirishga oqilona yondashsangiz, ratsional ifodalarni qanchalik soddalashtirish mumkinligini ko'rsatish.

Va endi, bularning barchasini bilganingizdan so'ng, keling, bugungi darsimizning asosiy mavzusiga - kasrli ratsional tengsizliklarni yechishga o'tamiz. Bundan tashqari, bunday tayyorgarlikdan so'ng, tengsizliklar yong'oq kabi bosiladi. :)

Ratsional tengsizliklarni yechishning asosiy usuli

Ratsional tengsizliklarni yechishda kamida ikkita yondashuv mavjud. Endi biz ulardan birini ko'rib chiqamiz - maktab matematika kursida umumiy qabul qilingan.

Lekin birinchi navbatda, bir muhim tafsilotga e'tibor qaratamiz. Barcha tengsizliklar ikki turga bo'linadi:

1. Qattiq: $f\left(x \right) \gt 0$ yoki $f\left(x \o'ng) \lt 0$;
2. Nostandart: $f\left(x \right)\ge 0$ yoki $f\left(x \o'ng)\le 0$.

Ikkinchi turdagi tengsizliklar birinchisiga osonlikcha tushiriladi, shuningdek tenglama:

Ushbu kichik "qo'shimcha" $f\left(x \right)=0$ to'ldirilgan nuqtalar kabi yoqimsiz narsaga olib keladi - biz ularni intervalli usulda uchratdik. Aks holda, qat'iy va qat'iy bo'lmagan tengsizliklar o'rtasida farq yo'q, shuning uchun universal algoritmni tahlil qilaylik:

1. Tengsizlik belgisining bir tomonida nolga teng bo'lmagan barcha elementlarni to'plang. Masalan, chap tomonda;
2. Barcha kasrlarni umumiy maxrajga keltiring (agar bunday kasrlar bir nechta bo'lsa), shunga o'xshashlarni keltiring. Keyin, agar iloji bo'lsa, son va maxrajga ajrating. U yoki bu tarzda biz $\frac(P\left(x \right))(Q\left(x \right))\vee 0$ ko`rinishdagi tengsizlikni olamiz, bunda belgi tengsizlik belgisidir.
3. Numeratorni nolga tenglashtiring: $P\left(x \right)=0$. Biz bu tenglamani yechib, $((x)_(1))$, $((x)_(2))$, $((x)_(3))$, ... ildizlarini olamiz. maxraj nolga teng emasligi: $Q\left(x \right)\ne 0$. Albatta, mohiyatan $Q\left(x \right)=0$ tenglamasini yechishimiz kerak va $x_(1)^(*)$, $x_(2)^(*) ildizlarini olamiz. $, $x_(3 )^(*)$, ... (haqiqiy masalalarda bunday ildizlar uchtadan ko'p bo'lmaydi).
4. Biz bu ildizlarning barchasini (yulduzchali va yulduzsiz) bitta raqam chizig'ida belgilaymiz va yulduzsiz ildizlar bo'yalgan, yulduzlilari esa teshilgan.
5. Biz ortiqcha va minus belgilarini joylashtiramiz, kerakli intervallarni tanlaymiz. Agar tengsizlik $f\left(x \right) \gt 0$ ko'rinishga ega bo'lsa, u holda javob "plyus" bilan belgilangan intervallar bo'ladi. Agar $f\left(x \right) \lt 0$ bo'lsa, u holda "minuslar" bilan intervallarni ko'rib chiqamiz.

Amaliyot shuni ko'rsatadiki, 2 va 4-bandlar eng katta qiyinchiliklarni keltirib chiqaradi - malakali o'zgarishlar va raqamlarni o'sish tartibida to'g'ri joylashtirish. Xo'sh, oxirgi bosqichda juda ehtiyot bo'ling: biz har doim belgilarga asoslanib joylashtiramiz tenglamalarga o'tishdan oldin yozilgan oxirgi tengsizlik. Bu intervalli usuldan meros bo'lib qolgan universal qoidadir.

Shunday qilib, sxema mavjud. Keling, mashq qilaylik.

Vazifa. Tengsizlikni yeching:

\[\frac(x-3)(x+7) \lt 0\]

Qaror. Bizda $f\left(x \right) \lt 0$ ko'rinishdagi qat'iy tengsizlik mavjud. Shubhasiz, bizning sxemamizdagi 1 va 2-bandlar allaqachon bajarilgan: tengsizlikning barcha elementlari chap tomonda to'plangan, hech narsani umumiy maxrajga tushirish kerak emas. Shunday qilib, uchinchi nuqtaga o'tamiz.

Numeratorni nolga qo'ying:

\[\boshlang(hatlang) & x-3=0; \\ &x=3. \end(tuzalash)\]

Va maxraj:

\[\boshlang(hatlang) & x+7=0; \\ & ((x)^(*))=-7. \\ \end (tekislash)\]

Bu joyda ko'pchilik tiqilib qoladi, chunki nazariy jihatdan ODZ talab qilganidek $x+7\ne 0$ yozish kerak (nolga bo'linib bo'lmaydi, hammasi shu). Ammo kelajakda biz maxrajdan kelgan nuqtalarni ajratib olamiz, shuning uchun siz hisob-kitoblaringizni yana bir bor murakkablashtirmasligingiz kerak - hamma joyda teng belgini yozing va xavotirlanmang. Buning uchun hech kim ball olib tashlamaydi. :)

To'rtinchi nuqta. Olingan ildizlarni raqamlar qatorida belgilaymiz:

Tengsizlik qat'iy bo'lgani uchun barcha nuqtalar teshiladi

Eslatma: barcha nuqtalar teshiladi, chunki dastlabki tengsizlik qat'iydir. Va bu erda endi muhim emas: bu nuqtalar hisoblagichdan yoki maxrajdan kelgan.

Xo'sh, belgilarga qarang. $((x)_(0)) \gt 3$ istalgan raqamni oling. Misol uchun, $((x)_(0))=100$ (lekin siz $((x)_(0))=3.1$ yoki $((x)_(0)) = olishi mumkin edi. 1\000\000$). Biz olamiz:

Shunday qilib, barcha ildizlarning o'ng tomonida biz ijobiy maydonga egamiz. Va har bir ildizdan o'tayotganda, belgi o'zgaradi (bu har doim ham shunday bo'lmaydi, lekin bu haqda keyinroq). Shuning uchun biz beshinchi nuqtaga o'tamiz: biz belgilarni joylashtiramiz va to'g'risini tanlaymiz:

Biz tenglamalarni echishdan oldin bo'lgan oxirgi tengsizlikka qaytamiz. Aslida, bu asl nusxaga to'g'ri keladi, chunki biz bu vazifada hech qanday o'zgarishlar qilmadik.

$f\left(x \right) \lt 0$ ko'rinishdagi tengsizlikni yechish zarur bo'lganligi sababli, men $x\intervalini \left(-7;3 \right)$da soya qildim - bu yagona. minus belgisi bilan belgilanadi. Bu javob.

Javob: $x\in \left(-7;3 \right)$

Ana xolos! Bu qiyinmi? Yo'q, qiyin emas. Darhaqiqat, bu oson ish edi. Keling, missiyani biroz murakkablashtiramiz va ko'proq "xayoliy" tengsizlikni ko'rib chiqamiz. Uni hal qilishda men endi bunday batafsil hisob-kitoblarni bermayman - men oddiygina asosiy fikrlarni aytib beraman. Umuman olganda, biz buni mustaqil ish yoki imtihonda qanday bajargan bo'lsak, shunday tartibga solamiz. :)

Vazifa. Tengsizlikni yeching:

\[\frac(\left(7x+1 \o'ng)\left(11x+2 \o'ng))(13x-4)\ge 0\]

Qaror. Bu $f\left(x \right)\ge 0$ ko'rinishidagi qat'iy bo'lmagan tengsizlikdir. Nolga teng bo'lmagan barcha elementlar chap tomonda to'plangan, har xil denominatorlar yo'q. Keling, tenglamalarga o'tamiz.

Hisoblagich:

\[\begin(hizala) & \left(7x+1 \o'ng)\left(11x+2 \o'ng)=0 \\ & 7x+1=0\O'ng strelka ((x)_(1))=-\ frac(1)(7); \\ & 11x+2=0\Oʻng yoʻl ((x)_(2))=-\frac(2)(11). \\ \end (tekislash)\]

Denominator:

\[\boshlang(tuzala) & 13x-4=0; \\ & 13x=4; \\ & ((x)^(*))=\frac(4)(13). \\ \end (tekislash)\]

Men bu muammoni qanday buzuq odam yaratganini bilmayman, lekin ildizlar unchalik yaxshi chiqmadi: ularni raqamlar qatorida joylashtirish qiyin bo'ladi. Va agar $((x)^(*))=(4)/(13)\;$ ildizi bilan hamma narsa ko'proq yoki kamroq aniq bo'lsa (bu yagona ijobiy raqam - o'ng tomonda bo'ladi), keyin $ ((x)_(1 ))=-(1)/(7)\;$ va $((x)_(2))=-(2)/(11)\;$ qoʻshimcha oʻrganishni talab qiladi: qaysi biri kattaroqmi?

Buni bilib olishingiz mumkin, masalan:

\[((x)_(1))=-\frac(1)(7)=-\frac(2)(14) \gt -\frac(2)(11)=((x)_(2) ))\]

Umid qilamanki, nima uchun sonli kasr $-(2)/(14)\; \gt -(2)/(11)\;$? Agar kerak bo'lsa, kasrlar bilan harakatlarni qanday bajarishni eslashni tavsiya etaman.

Va biz uchta ildizni raqamlar qatorida belgilaymiz:

Numeratordan nuqtalar soyalanadi, maxrajdan ular kesiladi

Biz belgilar qo'yamiz. Masalan, siz $((x)_(0))=1$ ni olishingiz va shu nuqtada belgini topishingiz mumkin:

\[\begin(align) & f\left(x \right)=\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4); \\ & f\left(1 \o'ng)=\frac(\left(7\cdot 1+1 \right)\left(11\cdot 1+2 \o'ng))(13\cdot 1-4)=\ frac(8\cdot 13)(9) \gt 0. \\\end(align)\]

Tenglamalardan oldingi oxirgi tengsizlik $f\left(x \right)\ge 0$ edi, shuning uchun bizni ortiqcha belgisi qiziqtiradi.

Biz ikkita to'plam oldik: biri oddiy segment, ikkinchisi esa raqamlar chizig'idagi ochiq nur.

Javob: $x\in \left[ -\frac(2)(11);-\frac(1)(7) \right]\bigcup \left(\frac(4)(13);+\infty \right )$

Eng o'ng oraliqdagi belgini topish uchun biz almashtiradigan raqamlar haqida muhim eslatma. Eng o'ngdagi ildizga yaqin raqamni almashtirish shart emas. Siz milliardlab yoki hatto "plyus-cheksizlik" ni olishingiz mumkin - bu holda, qavs, numerator yoki maxrajdagi ko'phadning belgisi faqat etakchi koeffitsient belgisi bilan belgilanadi.

Oxirgi tengsizlikdan $f\left(x \right)$ funksiyasini yana bir bor ko‘rib chiqamiz:

U uchta polinomni o'z ichiga oladi:

\[\begin(align) & ((P)_(1))\left(x \right)=7x+1; \\ & ((P)_(2))\chap(x \o'ng)=11x+2; \\ & Q\chap(x\o'ng)=13x-4. \end(tuzalash)\]

Ularning barchasi chiziqli binomiallar bo'lib, ularning barchasi ijobiy koeffitsientlarga ega (7, 11 va 13 raqamlar). Shuning uchun, juda katta raqamlarni almashtirganda, polinomlarning o'zi ham ijobiy bo'ladi. :)

Bu qoida haddan tashqari murakkab tuyulishi mumkin, lekin birinchi navbatda, biz juda oson muammolarni tahlil qilganimizda. Jiddiy tengsizliklarda "plyus-cheksizlik" almashtirish bizga $((x)_(0))=100$ standartidan ancha tezroq belgilarni aniqlash imkonini beradi.

Tez orada bunday qiyinchiliklarga duch kelamiz. Lekin, avvalo, kasrli ratsional tengsizliklarni yechishning muqobil usulini ko‘rib chiqamiz.

Alternativ usul

Bu texnikani menga shogirdlarimdan biri taklif qilgan. Men o'zim uni hech qachon ishlatmaganman, lekin amaliyot shuni ko'rsatdiki, ko'plab talabalar uchun tengsizliklarni shu tarzda hal qilish haqiqatan ham qulayroqdir.

Shunday qilib, asl ma'lumotlar bir xil. Biz kasrli ratsional tengsizlikni yechishimiz kerak:

\[\frac(P\left(x \o'ng))(Q\left(x \o'ng)) \gt 0\]

Keling, o'ylab ko'raylik: nima uchun $Q\left(x \right)$ ko'phad $P\left(x \right)$ polinomidan "yomonroq"? Nima uchun biz ildizlarning alohida guruhlarini (yulduzcha bilan va yulduzsiz) ko'rib chiqishimiz kerak, teshilgan nuqtalar haqida o'ylashimiz kerak va hokazo? Hammasi oddiy: kasrning ta'rif sohasi bor, unga ko'ra kasr faqat uning maxraji noldan farq qilganda ma'noga ega bo'ladi.

Aks holda, hisob va maxraj o'rtasida hech qanday farq yo'q: biz ham uni nolga tenglashtiramiz, ildizlarni qidiramiz, keyin ularni raqamlar qatorida belgilaymiz. Xo'sh, nima uchun kasr satrini (aslida, bo'linish belgisi) odatiy ko'paytirish bilan almashtirib, DHSning barcha talablarini alohida tengsizlik sifatida yozmaslik kerak? Masalan, bu kabi:

\[\frac(P\left(x \o'ng))(Q\left(x \o'ng)) \gt 0\O'ng strelka \chap\( \boshlang(hatlang) & P\left(x \o'ng)\cdot Q \left(x \right) \gt 0, \\ & Q\left(x \right)\ne 0. \\ \end(hizala) \o'ng.\]

Iltimos, diqqat qiling: bu yondashuv muammoni intervallar usuliga kamaytirishga imkon beradi, ammo bu yechimni umuman murakkablashtirmaydi. Axir, baribir, $Q\left(x \right)$ polinomini nolga tenglashtiramiz.

Keling, haqiqiy vazifalarda qanday ishlashini ko'rib chiqaylik.

Vazifa. Tengsizlikni yeching:

\[\frac(x+8)(x-11) \gt 0\]

Qaror. Shunday qilib, interval usuliga o'tamiz:

\[\frac(x+8)(x-11) \gt 0\O'ng strelka \chap\( \begin(align) & \left(x+8 \o'ng)\left(x-11 \o'ng) \gt 0 , \\ & x-11\ne 0. \\ \end(tuzala) \o'ngga.\]

Birinchi tengsizlik elementar yechiladi. Faqat har bir qavsni nolga qo'ying:

\[\begin(align) & x+8=0\O'ng strelka ((x)_(1))=-8; \\ & x-11=0\Oʻng strelka ((x)_(2))=11. \\ \end (tekislash)\]

Ikkinchi tengsizlik bilan hamma narsa oddiy:

Haqiqiy chiziqda $((x)_(1))$ va $((x)_(2))$ nuqtalarini belgilaymiz. Ularning barchasi teshilgan, chunki tengsizlik qat'iy:

To'g'ri nuqta ikki marta teshilgan bo'lib chiqdi. Bu odatiy.

$x=11$ nuqtaga e'tibor bering. Ma'lum bo'lishicha, u "ikki marta o'yilgan": bir tomondan, biz tengsizlikning jiddiyligi sababli, boshqa tomondan, ODZning qo'shimcha talabi tufayli uni o'chirib tashlaymiz.

Har holda, bu shunchaki teshilgan nuqta bo'ladi. Shuning uchun biz $\left(x+8 \right)\left(x-11 \right) \gt 0$ tengsizligining belgilarini qo'yamiz - biz tenglamalarni echishni boshlashdan oldin oxirgi ko'rganimiz:

Bizni ijobiy mintaqalar qiziqtiradi, chunki biz $f\left(x \right) \gt 0$ koʻrinishdagi tengsizlikni yechyapmiz va biz ularni ranglaymiz. Javobni yozishgina qoladi.

Javob. $x\in \left(-\infty;-8 \right)\bigcup \left(11;+\infty \o'ng)$

Ushbu yechimni misol sifatida ishlatib, men sizni yangi boshlanuvchilar orasida keng tarqalgan xatodan ogohlantirmoqchiman. Ya'ni: tengsizliklarda hech qachon qavs ochmang! Aksincha, hamma narsani hisobga olishga harakat qiling - bu yechimni soddalashtiradi va sizni juda ko'p muammolardan xalos qiladi.

Endi qiyinroq narsani sinab ko'raylik.

Vazifa. Tengsizlikni yeching:

\[\frac(\left(2x-13 \o'ng)\left(12x-9 \o'ng))(15x+33)\le 0\]

Qaror. Bu $f\left(x \right)\le 0$ shaklining qat'iy bo'lmagan tengsizligi, shuning uchun bu erda to'ldirilgan nuqtalarni diqqat bilan kuzatib borishingiz kerak.

Keling, interval usuliga o'tamiz:

\[\left\( \begin(hizala) & \left(2x-13 \o'ng)\left(12x-9 \o'ng)\left(15x+33 \o'ng)\le 0, \\ & 15x+33\ ne 0. \\ \end(tuzalash) \o'ngga.\]

Keling, tenglamaga o'tamiz:

\[\boshlang(hizalang) & \left(2x-13 \o'ng)\left(12x-9 \o'ng)\left(15x+33 \o'ng)=0 \\ & 2x-13=0\O'ng strelka ((x) )_(1))=6,5; \\ & 12x-9=0\Oʻng koʻrsatkich ((x)_(2))=0,75; \\ & 15x+33=0\Oʻng koʻrsatkich ((x)_(3))=-2,2. \\ \end (tekislash)\]

Biz qo'shimcha talabni hisobga olamiz:

Olingan barcha ildizlarni raqamlar qatorida belgilaymiz:

Agar nuqta bir vaqtning o'zida teshilgan va to'ldirilgan bo'lsa, u teshilgan hisoblanadi.

Shunga qaramay, ikkita nuqta bir-birining ustiga tushadi - bu normal holat, har doim shunday bo'ladi. Faqat teshilgan va to'ldirilgan deb belgilangan nuqta aslida teshilgan nuqta ekanligini tushunish muhimdir. Bular. "Tuymoq" "bo'yash"dan ko'ra kuchliroq harakatdir.

Bu mutlaqo mantiqiy, chunki ponksiyon orqali biz funktsiya belgisiga ta'sir qiladigan nuqtalarni belgilaymiz, lekin o'zlari javobda qatnashmaydi. Va agar biror nuqtada raqam bizga mos kelmay qolsa (masalan, u ODZga tushmasa), biz uni vazifaning oxirigacha ko'rib chiqishdan o'chirib tashlaymiz.

Umuman olganda, falsafa qilishni to'xtating. Biz belgilarni joylashtiramiz va minus belgisi bilan belgilangan intervallarni bo'yab qo'yamiz:

Javob. $x\in \left(-\infty ;-2,2 \right)\bigcup \left[ 0,75;6,5 \right]$.

Va yana sizning e'tiboringizni ushbu tenglamaga qaratmoqchiman:

\[\chap(2x-13 \o'ng)\chap(12x-9 \o'ng)\chap(15x+33 \o'ng)=0\]

Yana bir bor: bunday tenglamalarda hech qachon qavs ochmang! Siz buni faqat o'zingiz uchun qiyinlashtirasiz. Esingizda bo'lsin: omillarning kamida bittasi nolga teng bo'lsa, mahsulot nolga teng. Binobarin, bu tenglama oddiygina bir nechta kichikroqlarga "tushadi", biz oldingi masalada hal qildik.

Ildizlarning ko'pligini hisobga olgan holda

Oldingi masalalardan shuni ko'rish mumkinki, aniq bo'lmagan tengsizliklar eng qiyin, chunki ularda siz to'ldirilgan nuqtalarni kuzatib borishingiz kerak.

Ammo dunyoda bundan ham katta yovuzlik bor - bu tengsizliklarning bir nechta ildizlari. Bu erda allaqachon ba'zi to'ldirilgan nuqtalarga amal qilish kerak emas - bu erda tengsizlik belgisi xuddi shu nuqtalardan o'tayotganda to'satdan o'zgarmasligi mumkin.

Biz bu darsda hali shunga o'xshash narsalarni ko'rib chiqmadik (garchi shunga o'xshash muammo ko'pincha intervalli usulda uchragan bo'lsa ham). Shunday qilib, keling, yangi ta'rifni kiritamiz:

Ta'rif. $((\left(x-a \right))^(n))=0$ tenglamaning ildizi $x=a$ ga teng va $n$-chi koʻplikning ildizi deyiladi.

Aslida, biz ko'plikning aniq qiymatiga unchalik qiziqmaymiz. Bitta muhim narsa - bu $n$ soni juft yoki toq. Chunki:

1. Agar $x=a$ juft koʻplikning ildizi boʻlsa, u holda funksiyaning belgisi u orqali oʻtganda oʻzgarmaydi;
2. Va aksincha, agar $x=a$ toq ko'plikning ildizi bo'lsa, u holda funktsiyaning belgisi o'zgaradi.

Toq ko'plik ildizining alohida holati bu darsda ko'rib chiqilgan barcha oldingi muammolardir: u erda ko'plik hamma joyda bittaga teng.

Va yana. Muammolarni hal qilishni boshlashdan oldin, men sizning e'tiboringizni tajribali talaba uchun tushunarli bo'lib ko'rinadigan, ammo ko'plab yangi boshlanuvchilarni ahmoqlikka olib keladigan bitta noziklikka qaratmoqchiman. Aynan:

Koʻplik ildizi $n$ faqat butun ifoda shu darajaga koʻtarilganda yuzaga keladi: $((\left(x-a \right))^(n))$, $\left(((x)^( n) emas. )-a\right)$.

Yana bir bor: $((\left(x-a \right))^(n))$ qavs bizga $n$ koʻpligining $x=a$ ildizini beradi, lekin qavs $\left(((x)^() n)) -a \right)$ yoki tez-tez sodir bo'lganidek, $(a-((x)^(n)))$ bizga birinchi ko'paytmaning ildizini (yoki ikkita ildizni, agar $n$ juft bo'lsa) beradi , $n$ ga nima teng bo'lishidan qat'iy nazar.

Taqqoslash:

\[((\chap(x-3 \o'ng))^(5))=0\O'ng strelka x=3\chap(5k \o'ng)\]

Bu erda hamma narsa aniq: butun qavs beshinchi kuchga ko'tarildi, shuning uchun chiqishda biz beshinchi darajaning ildizini oldik. Endi esa:

\[\left(((x)^(2))-4 \o'ng)=0\O'ng yo'l ((x)^(2))=4\O'ng strelka x=\pm 2\]

Bizda ikkita ildiz bor, lekin ularning ikkalasi ham birinchi ko'plikka ega. Yoki mana yana biri:

\[\left(((x)^(10))-1024 \o'ng)=0\O'ng yo'l ((x)^(10))=1024\O'ng yo'l x=\pm 2\]

Va o'ninchi daraja bilan adashmang. Asosiysi, 10 - juft son, shuning uchun bizda ikkita ildiz bor va ularning ikkalasi ham yana birinchi ko'paytmaga ega.

Umuman olganda, ehtiyot bo'ling: ko'plik faqat qachon sodir bo'ladi daraja faqat o'zgaruvchiga emas, balki butun qavsga tegishli.

Vazifa. Tengsizlikni yeching:

\[\frac(((x)^(2))((\left(6-x \o'ng))^(3))\left(x+4 \o'ng))(((\left(x+7) \o'ng))^(5)))\ge 0\]

Qaror. Keling, uni muqobil usulda - xususiydan mahsulotga o'tish orqali hal qilishga harakat qilaylik:

\[\left\( \begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \o'ng)\cdot ( (\left(x+7 \o'ng))^(5))\ge 0, \\ & ((\left(x+7 \o'ng))^(5))\ne 0. \\ \end(tekislash) )\o‘ng.\]

Interval usuli yordamida birinchi tengsizlik bilan ishlaymiz:

\[\begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \o'ng)\cdot ((\left() x+7 \right))^(5))=0; \\ & ((x)^(2))=0\O'ng strelka x=0\chap(2k \o'ng); \\ & ((\chap(6-x \o'ng))^(3))=0\O'ngga x=6\chap(3k \o'ng); \\ & x+4=0\Oʻng strelka x=-4; \\ & ((\chap(x+7 \o'ng))^(5))=0\O'ngga x=-7\chap(5k \o'ng). \\ \end (tekislash)\]

Bundan tashqari, biz ikkinchi tengsizlikni hal qilamiz. Aslida, biz buni allaqachon hal qildik, ammo sharhlovchilar yechimda xato topmasliklari uchun uni yana hal qilish yaxshiroqdir:

\[((\chap(x+7 \o'ng))^(5))\ne 0\O'ng strelka x\ne -7\]

E'tibor bering, oxirgi tengsizlikda ko'plik yo'q. Haqiqatan ham: raqamlar chizig'idagi $x=-7$ nuqtani necha marta kesib tashlashning qanday farqi bor? Kamida bir marta, kamida besh marta - natija bir xil bo'ladi: teshilgan nuqta.

Keling, raqamlar qatorida olgan hamma narsani qayd qilaylik:

Aytganimdek, $x=-7$ nuqtasi oxir-oqibat o'chiriladi. Ko'paytmalar tengsizlikni intervalli usul bilan hal qilish asosida tartibga solinadi.

Belgilarni joylashtirish qoladi:

$x=0$ nuqta juft koʻplikning ildizi boʻlgani uchun u orqali oʻtganda belgisi oʻzgarmaydi. Qolgan nuqtalar g'alati ko'plikka ega va ular bilan hamma narsa oddiy.

Javob. $x\in \left(-\infty;-7 \right)\bigcup \left[ -4;6 \right]$

Yana $x=0$ ga e'tibor bering. Bir tekis ko'pligi tufayli qiziqarli effekt paydo bo'ladi: uning chap tomonidagi hamma narsa bo'yalgan, o'ngda - ham, nuqta o'zi esa butunlay bo'yalgan.

Natijada, javobni yozishda uni izolyatsiya qilish kerak emas. Bular. $x\in \left[ -4;0 \right]\bigcup \left[ 0;6 \right]$ kabi biror narsa yozishingiz shart emas (garchi rasmiy ravishda bunday javob ham to'g'ri bo'lar edi). Buning o'rniga biz darhol $x\in \left[ -4;6 \right]$ deb yozamiz.

Bunday ta'sir faqat ko'plikning ildizlari uchun mumkin. Va keyingi vazifada biz bu ta'sirning teskari "namoyishiga" duch kelamiz. Tayyormisiz?

Vazifa. Tengsizlikni yeching:

\[\frac(((\left(x-3 \o'ng))^(4))\left(x-4 \o'ng))(((\left(x-1 \o'ng))^(2)) \left(7x-10-((x)^(2)) \right))\ge 0\]

Qaror. Bu safar biz standart sxemaga amal qilamiz. Numeratorni nolga qo'ying:

\[\begin(align) & ((\left(x-3 \right))^(4))\left(x-4 \right)=0; \\ & ((\chap(x-3 \o'ng))^(4))=0\O'ng strelka ((x)_(1))=3\chap(4k \o'ng); \\ & x-4=0\Oʻng strelka ((x)_(2))=4. \\ \end (tekislash)\]

Va maxraj:

\[\begin(align) & ((\left(x-1 \right))^(2))\left(7x-10-((x)^(2)) \o'ng)=0; \\ & ((\chap(x-1 \o'ng))^(2))=0\O'ngga x_(1)^(*)=1\left(2k \o'ng); \\ & 7x-10-((x)^(2))=0\Oʻng tomon x_(2)^(*)=5;\ x_(3)^(*)=2. \\ \end (tekislash)\]

Biz $f\left(x \right)\ge 0$ ko'rinishdagi qat'iy bo'lmagan tengsizlikni yechayotganimiz sababli, maxrajdan (yulduzchalar mavjud) ildizlar kesiladi va hisoblagichdan olingan ildizlar bo'yaladi. .

Biz belgilarni joylashtiramiz va "ortiqcha" bilan belgilangan joylarni silaymiz:

$x=3$ nuqta ajratilgan. Bu javobning bir qismi

Yakuniy javobni yozishdan oldin, rasmga diqqat bilan qarang:

1. $x=1$ nuqta teng ko'plikka ega, lekin o'zi teshilgan. Shuning uchun javobda uni izolyatsiya qilish kerak bo'ladi: siz $x\da emas, balki \left(-\infty ;1 \right)\bigcup \left(1;2 \right)$da $x\ni yozishingiz kerak. \left(-\ infty ;2\right)$.
2. $x=3$ nuqta ham teng ko'plikka ega va soyalangan. Belgilarning joylashuvi shuni ko'rsatadiki, nuqtaning o'zi bizga mos keladi, lekin chapga va o'ngga bir qadam - va biz o'zimizni aniq bizga mos kelmaydigan sohada topamiz. Bunday nuqtalar ajratilgan deb ataladi va $x\in \left\( 3 \right\)$ shaklida yoziladi.

Olingan barcha qismlarni umumiy to'plamga birlashtiramiz va javobni yozamiz.

Javob: $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;5 \right) $

Ta'rif. Tengsizlikni yechish degani uning barcha yechimlari to‘plamini toping, yoki bu to'plam bo'sh ekanligini isbotlang.

Ko'rinadi: bu erda nima tushunarsiz bo'lishi mumkin? Ha, gap shundaki, to'plamlar turli yo'llar bilan belgilanishi mumkin. Keling, oxirgi masalaga javobni qayta yozamiz:

Biz yozilganlarni tom ma'noda o'qiymiz. "X" o'zgaruvchisi ma'lum to'plamga tegishli bo'lib, u to'rtta alohida to'plamning birlashishi ("U" belgisi) bilan olinadi:

• $\left(-\infty ;1 \right)$ oralig'i, bu so'zma-so'z "barcha raqamlar birdan kichik, lekin bitta emas" degan ma'noni anglatadi;
• Interval $\left(1;2 \right)$, ya'ni. "1 dan 2 gacha bo'lgan barcha raqamlar, lekin 1 va 2 raqamlarining o'zi emas";
• To'plam $\left\( 3 \right\)$, bitta raqamdan iborat - uchta;
• $\left[ 4;5 \right)$ oralig'i 4 dan 5 gacha bo'lgan barcha raqamlarni, shuningdek, 4 ni o'z ichiga oladi, lekin 5 emas.

Bu erda uchinchi nuqta qiziq. Cheksiz sonlar to'plamini belgilaydigan va faqat shu to'plamlarning chegaralarini bildiruvchi intervallardan farqli o'laroq, $\left\( 3 \right\)$ to'plami sanab o'tish orqali aniq bitta raqamni belgilaydi.

Biz to'plamga kiritilgan aniq raqamlarni sanab o'tayotganimizni tushunish uchun (va chegaralarni yoki boshqa narsalarni belgilamasdan), jingalak qavslardan foydalaniladi. Misol uchun, $\left\( 1;2 \right\)$ yozuvi aynan "ikki raqamdan iborat: 1 va 2" to'plamini anglatadi, lekin 1 dan 2 gacha bo'lgan segmentni emas. Hech qanday holatda bu tushunchalarni chalkashtirmang. .

Ko'plikni qo'shish qoidasi

Xo'sh, bugungi dars oxirida Pavel Berdovdan bir oz qalay. :)

Ehtiyotkor talabalar, ehtimol, allaqachon o'zlariga savol berishgan: agar hisoblagich va maxrajda bir xil ildizlar topilsa nima bo'ladi? Shunday qilib, quyidagi qoida ishlaydi:

Bir xil ildizlarning ko'pligi qo'shiladi. Har doim. Bu ildiz ham sanoqda, ham maxrajda sodir bo'lsa ham.

Ba'zan gapirishdan ko'ra qaror qabul qilish yaxshiroqdir. Shunday qilib, biz quyidagi muammoni hal qilamiz:

Vazifa. Tengsizlikni yeching:

\[\frac(((x)^(2))+6x+8)(\left(((x)^(2))-16 \o'ng)\left((x)^(2))+ 9x+14 \o'ng))\ge 0\]

\[\begin(align) & ((x)^(2))+6x+8=0 \\ & ((x)_(1))=-2;\ ((x)_(2))= -4. \\ \end (tekislash)\]

Hozircha, hech qanday maxsus narsa yo'q. Maxrajni nolga qo'ying:

\[\begin(align) & \left(((x)^(2))-16 \right)\left((x)^(2))+9x+14 \o'ng)=0 \\ & ( (x)^(2))-16=0\O‘ng strelka x_(1)^(*)=4;\ x_(2)^(*)=-4; \\ & ((x)^(2))+9x+14=0\Oʻngga x_(3)^(*)=-7;\ x_(4)^(*)=-2. \\ \end (tekislash)\]

Ikkita bir xil ildiz topildi: $((x)_(1))=-2$ va $x_(4)^(*)=-2$. Ikkalasi ham birinchi ko'plikka ega. Shuning uchun biz ularni bitta ildiz bilan almashtiramiz $x_(4)^(*)=-2$, lekin ko'pligi 1+1=2.

Bundan tashqari, bir xil ildizlar ham mavjud: $((x)_(2))=-4$ va $x_(2)^(*)=-4$. Ular ham birinchi ko'plikdir, shuning uchun faqat $x_(2)^(*)=-4$ ko'plik 1+1=2 qoladi.

E'tibor bering: ikkala holatda ham biz "kesilgan" ildizni qoldirdik va "bo'yalgan" ildizni ko'rib chiqishdan chiqarib tashladik. Chunki dars boshida ham biz kelishib oldik: agar nuqta bir vaqtning o'zida teshib qo'yilgan va bo'yalgan bo'lsa, biz baribir uni teshilgan deb hisoblaymiz.

Natijada, bizda to'rtta ildiz bor va ularning barchasi o'yilgan bo'lib chiqdi:

\[\begin(align) & x_(1)^(*)=4; \\ & x_(2)^(*)=-4\left(2k \o'ng); \\ & x_(3)^(*)=-7; \\ & x_(4)^(*)=-2\chap(2k \o'ng). \\ \end (tekislash)\]

Biz ularni ko'plikni hisobga olgan holda raqamlar qatorida belgilaymiz:

Biz belgilarni joylashtiramiz va bizni qiziqtirgan joylarga bo'yab qo'yamiz:

Hamma narsa. Izolyatsiya qilingan nuqtalar va boshqa buzilishlar yo'q. Javobni yozishingiz mumkin.

Javob. $x\in \left(-\infty ;-7 \right)\bigcup \left(4;+\infty \right)$.

ko'paytirish qoidasi

Ba'zida bundan ham noxush holat yuzaga keladi: bir nechta ildizga ega bo'lgan tenglamaning o'zi ma'lum bir kuchga ko'tariladi. Bu barcha asl ildizlarning ko'pligini o'zgartiradi.

Bu kamdan-kam uchraydi, shuning uchun ko'pchilik talabalar bunday muammolarni hal qilishda tajribaga ega emaslar. Va bu erda qoida:

Tenglama $n$ darajaga ko'tarilsa, uning barcha ildizlarining ko'pligi ham $n$ marta ortadi.

Boshqacha qilib aytadigan bo'lsak, kuchga ko'tarilish ko'paytmalarni bir xil kuchga ko'paytirishga olib keladi. Keling, ushbu qoidani misol qilib olaylik:

Vazifa. Tengsizlikni yeching:

\[\frac(x((\left(((x)^(2))-6x+9 \o'ng))^(2))((\left(x-4 \o'ng))^(5)) )(((\left(2-x \o'ng))^(3))((\left(x-1 \o'ng))^(2)))\le 0\]

Qaror. Numeratorni nolga qo'ying:

Faktorlarning kamida bittasi nolga teng bo'lganda mahsulot nolga teng bo'ladi. Birinchi multiplikator bilan hamma narsa aniq: $x=0$. Va bu erda muammolar boshlanadi:

\[\begin(align) & ((\left(((x)^(2))-6x+9 \o'ng))^(2))=0; \\ & ((x)^(2))-6x+9=0\chap(2k \o'ng); \\ & D=((6)^(3))-4\cdot 9=0 \\ & ((x)_(2))=3\left(2k \o'ng)\left(2k \o'ng) \ \ & ((x)_(2))=3\chap(4k \o'ng) \\ \end(tuzala)\]

Ko'rib turganingizdek, $((x)^(2))-6x+9=0$ tenglama ikkinchi ko'plikning yagona ildiziga ega: $x=3$. Keyin butun tenglama kvadratga aylanadi. Demak, ildizning ko'pligi $2\cdot 2=4$ bo'ladi, biz buni nihoyat yozib oldik.

\[((\chap(x-4 \o'ng))^(5))=0\O'ng strelka x=4\chap(5k \o'ng)\]

Maxraj bilan ham muammo yo'q:

\[\begin(align) & ((\left(2-x \right))^(3))((\left(x-1 \right))^(2))=0; \\ & ((\left(2-x \o'ng))^(3))=0\O'ngga x_(1)^(*)=2\left(3k \o'ng); \\ & ((\chap(x-1 \o'ng))^(2))=0\O'ngga x_(2)^(*)=1\chap(2k \o'ng). \\ \end (tekislash)\]

Hammasi bo'lib biz besh ochko oldik: ikkitasi zarba berdi va uchtasi to'ldiriladi. Numerator va maxrajda mos keladigan ildizlar yo'q, shuning uchun biz ularni faqat raqamlar qatorida belgilaymiz:

Biz belgilarni ko'plikni hisobga olgan holda tartibga solamiz va bizni qiziqtirgan intervallarni bo'yab turamiz:

Yana bitta ajratilgan nuqta va bitta teshilgan

Hatto ko'plikning ildizlari tufayli biz yana bir nechta "nostandart" elementlarni oldik. Bu $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)$, $x\in \left[ 0;2 \right)$ emas, shuningdek, ajratilgan nuqta $ x\in \chap\( 3 \o'ng\)$.

Javob. $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;+\infty \right)$

Ko'rib turganingizdek, hamma narsa unchalik qiyin emas. Asosiysi, e'tibor. Ushbu darsning oxirgi qismi o'zgarishlarga bag'ishlangan - biz boshida muhokama qilgan narsalar.

Oldindan konversiyalar

Ushbu bo'limda biz muhokama qiladigan tengsizliklar murakkab emas. Biroq, oldingi vazifalardan farqli o'laroq, bu erda siz ratsional kasrlar nazariyasidan ko'nikmalarni qo'llashingiz kerak bo'ladi - faktorizatsiya va umumiy maxrajga qisqartirish.

Biz bugungi darsning boshida bu masalani batafsil muhokama qildik. Agar bu nima haqida ekanligini tushunganingizga ishonchingiz komil bo'lmasa, men sizga qaytib, takrorlashni tavsiya qilaman. Chunki kasrlarni ayirboshlashda "suzib" ketsangiz, tengsizliklarni yechish usullarini ko'paytirishdan ma'no yo'q.

Aytgancha, uy vazifasida ham shunga o'xshash vazifalar ko'p bo'ladi. Ular alohida bo'limga joylashtirilgan. Va u erda siz juda oddiy bo'lmagan misollarni topasiz. Ammo bu uy vazifasida bo'ladi, lekin endi bir nechta tengsizliklarni tahlil qilaylik.

Vazifa. Tengsizlikni yeching:

\[\frac(x)(x-1)\le \frac(x-2)(x)\]

Qaror. Hammasini chapga siljitish:

\[\frac(x)(x-1)-\frac(x-2)(x)\le 0\]

Biz umumiy maxrajga qisqartiramiz, qavslarni ochamiz, hisoblagichga o'xshash shartlarni beramiz:

\[\begin(align) & \frac(x\cdot x)(\left(x-1 \right)\cdot x)-\frac(\left(x-2 \o'ng)\left(x-1 \ o'ng))(x\cdot \left(x-1 \o'ng))\le 0; \\ & \frac(((x)^(2))-\left(((x)^(2))-2x-x+2 \o'ng))(x\left(x-1 \o'ng)) \le0; \\ & \frac(((x)^(2))-((x)^(2))+3x-2)(x\left(x-1 \o'ng))\le 0; \\ & \frac(3x-2)(x\left(x-1 \o'ng))\le 0. \\\end(align)\]

Endi bizda klassik kasrli ratsional tengsizlik bor, uni hal qilish endi qiyin emas. Men uni muqobil usul bilan - intervallar usuli bilan hal qilishni taklif qilaman:

\[\begin(align) & \left(3x-2 \right)\cdot x\cdot \left(x-1 \right)=0; \\ & ((x)_(1))=\frac(2)(3);\ ((x)_(2))=0;\ ((x)_(3))=1. \\ \end (tekislash)\]

Maxrajdan kelib chiqadigan cheklovni unutmang:

Biz raqamlar qatorida barcha raqamlar va cheklovlarni belgilaymiz:

Barcha ildizlarning birinchi ko'pligi bor. Hammasi joyida. Biz shunchaki belgilarni joylashtiramiz va kerakli joylarni bo'yab qo'yamiz:

Bu hammasi. Javobni yozishingiz mumkin.

Javob. $x\in \left(-\infty ;0 \right)\bigcup \left[ (2)/(3)\;;1 \right)$.

Albatta, bu juda oddiy misol edi. Shunday qilib, endi muammoni batafsil ko'rib chiqaylik. Aytgancha, bu vazifaning darajasi 8-sinfda ushbu mavzu bo'yicha mustaqil va nazorat ishlariga juda mos keladi.

Vazifa. Tengsizlikni yeching:

\[\frac(1)((x)^(2))+8x-9)\ge \frac(1)(3((x)^(2))-5x+2)\]

Qaror. Hammasini chapga siljitish:

\[\frac(1)((x)^(2))+8x-9)-\frac(1)(3((x)^(2))-5x+2)\ge 0\]

Ikkala kasrni umumiy maxrajga keltirishdan oldin bu maxrajlarni omillarga ajratamiz. To'satdan bir xil qavslar chiqadimi? Birinchi maxraj bilan bu oson:

\[((x)^(2))+8x-9=\chap(x-1 \o'ng)\chap(x+9 \o'ng)\]

Ikkinchisi biroz qiyinroq. Kasr topilgan qavsga doimiy ko'paytuvchini qo'shing. Esingizda bo'lsin: asl polinomda butun son koeffitsientlari bor edi, shuning uchun faktorizatsiya ham butun son koeffitsientlariga ega bo'lish ehtimoli katta (aslida, diskriminant irratsional bo'lmagan holatlar bundan mustasno).

\[\begin(align) & 3((x)^(2))-5x+2=3\left(x-1 \o'ng)\left(x-\frac(2)(3) \o'ng)= \\ & =\chap(x-1 \o'ng)\chap(3x-2 \o'ng) \end(hizala)\]

Ko'rib turganingizdek, umumiy qavs mavjud: $\left(x-1 \right)$. Biz tengsizlikka qaytamiz va ikkala kasrni umumiy maxrajga keltiramiz:

\[\begin(align) & \frac(1)(\left(x-1 \o'ng)\left(x+9 \o'ng))-\frac(1)(\left(x-1 \o'ng)\ chap(3x-2\o'ng))\ge 0; \\ & \frac(1\cdot \left(3x-2 \o'ng)-1\cdot \left(x+9 \right))(\left(x-1 \o'ng)\chap(x+9 \o'ng) )\left(3x-2 \right))\ge 0; \\ & \frac(3x-2-x-9)(\left(x-1 \o'ng)\left(x+9 \o'ng)\left(3x-2 \o'ng))\ge 0; \\ & \frac(2x-11)(\left(x-1 \o'ng)\left(x+9 \o'ng)\left(3x-2 \o'ng))\ge 0; \\ \end (tekislash)\]

Maxrajni nolga qo'ying:

\[\begin(align) & \left(x-1 \right)\left(x+9 \right)\left(3x-2 \o'ng)=0; \\ & x_(1)^(*)=1;\ x_(2)^(*)=-9;\ x_(3)^(*)=\frac(2)(3) \\ \end( tekislash)\]

Ko'plik va mos keladigan ildizlar yo'q. To'g'ri chiziqda to'rtta raqamni belgilaymiz:

Biz belgilarni joylashtiramiz:

Javobni yozamiz.

Javob: $x\in \left(-\infty ;-9 \right)\bigcup \left((2)/(3)\;;1 \right)\bigcup \left[ 5,5;+\infty \ o'ng) $.

Hammasi! Xuddi shunday, men ushbu satrgacha o'qidim. :)

Chiziqli tengsizliklar deyiladi chap va o'ng qismlari noma'lum qiymatga nisbatan chiziqli funktsiyalardir. Bularga, masalan, tengsizliklar kiradi:

2x-1-x+3; 7x0;

5 >4 - 6x 9- x< x + 5 .

1) Qattiq tengsizliklar: ax+b>0 yoki ax+b<0

2) qat'iy bo'lmagan tengsizliklar: ax+b≤0 yoki ax+b≫ 0

Keling, bu vazifani bajaraylik. Parallelogrammaning bir tomoni 7 sm. Paralelogrammaning perimetri 44 sm dan katta bo'lishi uchun boshqa tomonining uzunligi qancha bo'lishi kerak?

Istalgan tomon bo'lsin X qarang Bu holda parallelogramm perimetri (14+2x) bilan ifodalanadi.14+2x>44 tengsizlik parallelogramm perimetri masalasining matematik modelidir. Agar bu tengsizlikda biz o'zgaruvchini almashtiramiz X masalan, 16 raqami bo'yicha, keyin biz to'g'ri raqamli tengsizlikni olamiz 14 + 32\u003e 44. Bunday holda, biz 16 raqami 14 + 2x\u003e 44 tengsizlikning yechimi ekanligini aytamiz.

Tengsizlik yechimi o‘zgaruvchining haqiqiy sonli tengsizlikka aylantiruvchi qiymatini ayting.

Shuning uchun raqamlarning har biri 15.1; 20;73 14 + 2x > 44 tengsizligining yechimi vazifasini bajaradi va masalan, 10 soni uning yechimi emas.

Tengsizlikni yeching uning barcha yechimlarini o'rnatish yoki echimlar mavjud emasligini isbotlash demakdir.

Tengsizlikning yechimini shakllantirish tenglamaning ildizini shakllantirishga o'xshaydi. Va shunga qaramay, "tengsizlikning ildizi" ni belgilash odatiy hol emas.

Raqamli tengliklarning xossalari bizga tenglamalarni yechishga yordam berdi. Xuddi shunday, sonli tengsizliklarning xossalari tengsizliklarni hal qilishga yordam beradi.

Tenglamani yechishda biz uni boshqa, soddaroq, ammo berilgan tenglamaga o'zgartiramiz. Xuddi shunday, tengsizliklar uchun javob topiladi. Tenglamani unga ekvivalent tenglamaga o'zgartirganda, ular tenglamaning bir qismidan teskarisiga hadlarni o'tkazish va tenglamaning ikkala qismini bir xil nolga teng bo'lmagan songa ko'paytirish teoremasidan foydalanadilar. Tengsizlikni yechishda u bilan tenglama o'rtasida sezilarli farq mavjud bo'lib, bu tenglamaning har qanday yechimini uni dastlabki tenglamaga almashtirish orqali tekshirish mumkinligidadir. Tengsizliklarda bunday usul yo'q, chunki dastlabki tengsizlikka cheksiz ko'p echimlarni almashtirish mumkin emas. Shuning uchun, muhim tushuncha, bu o'qlar mavjud<=>ekvivalent yoki ekvivalent o'zgarishlarning belgisidir. Transformatsiya deyiladi ekvivalent yoki ekvivalent agar ular qarorlar to'plamini o'zgartirmasalar.

Tengsizliklarni yechish uchun shunga o'xshash qoidalar.

Agar biron-bir atama tengsizlikning bir qismidan ikkinchisiga o'tkazilsa, uning belgisini qarama-qarshisi bilan almashtirsa, biz berilgan tengsizlikka ekvivalent bo'lamiz.

Agar tengsizlikning ikkala qismi bir xil musbat songa ko'paytirilsa (bo'linsa), u holda biz berilgan tengsizlikka ega bo'lamiz.

Agar tengsizlikning ikkala qismi bir xil manfiy songa ko'paytirilsa (bo'linsa), tengsizlik belgisini qarama-qarshisi bilan almashtirsa, biz berilgan tengsizlikka ekvivalent bo'lamiz.

Bulardan foydalanish qoidalar quyidagi tengsizliklarni hisoblaymiz.

1) Keling, tengsizlikni tahlil qilaylik 2x - 5 > 9.

Bu chiziqli tengsizlik, uning yechimini toping va asosiy tushunchalarni muhokama qiling.

2x - 5 > 9<=>2x > 14(5 qarama-qarshi belgi bilan chap tomonga ko'chirildi), keyin biz hamma narsani 2 ga bo'ldik va bizda bor x > 7. Eksaga yechimlar to'plamini qo'llaymiz x

Biz ijobiy yo'naltirilgan nurni oldik. Yechimlar to‘plamini tengsizlik ko‘rinishida ham qayd etamiz x > 7, yoki x(7; ∞) oraliq sifatida. Va bu tengsizlikning alohida yechimi qanday? Masalan, x=10 bu tengsizlikning alohida yechimi, x=12 bu tengsizlikning alohida yechimi hamdir.

Ko'p maxsus echimlar mavjud, ammo bizning vazifamiz barcha echimlarni topishdir. Va echimlar odatda cheksizdir.

Keling, tahlil qilaylik 2-misol:

2) Tengsizlikni yeching 4a - 11 > a + 13.

Keling, buni hal qilaylik: a bir tomonga o'ting 11 boshqa tomonga o'ting, biz 3a ni olamiz< 24, и в результате после деления обеих частей на 3 tengsizlik shaklga ega a<8 .

4a - 11 > a + 13<=>3a< 24 <=>a< 8 .

Shuningdek, biz to'plamni ko'rsatamiz a< 8 , lekin allaqachon o'qda a.

Javob a tengsizlik sifatida yoziladi< 8, либо a(-∞;8), 8 yoqilmaydi.

Bo'shliq usuli kasrli ratsional tengsizliklarni yechishning oddiy usulidir. Bu o'zgaruvchiga bog'liq bo'lgan ratsional (yoki kasr-ratsional) ifodalarni o'z ichiga olgan tengsizliklarning nomi.

1. Masalan, quyidagi tengsizlikni ko'rib chiqaylik

Intervalli usul uni bir necha daqiqada hal qilishga imkon beradi.

Bu tengsizlikning chap tomonida kasrli ratsional funksiya joylashgan. Ratsional, chunki unda na ildizlar, na sinuslar, na logarifmlar mavjud - faqat ratsional ifodalar. O'ng tomonda nol.

Intervalli usul kasrli ratsional funksiyaning quyidagi xossasiga asoslanadi.

Kasr ratsional funktsiya belgisini faqat nolga teng yoki mavjud bo'lmagan nuqtalarda o'zgartirishi mumkin.

Kvadrat uch a'zo qanday faktorlarga ajratilganligini, ya'ni shaklning ifodasini eslang.

Kvadrat tenglamaning ildizlari qayerda va.

Biz o'qni chizamiz va hisoblagich va maxraj yo'qolgan nuqtalarni joylashtiramiz.

Maxrajning nollari va teshilgan nuqtalardir, chunki bu nuqtalarda tengsizlikning chap tomonidagi funktsiya aniqlanmagan (nolga bo'linib bo'lmaydi). Numerator va - nollari soyalanadi, chunki tengsizlik qat'iy emas. For va bizning tengsizligimiz qondiriladi, chunki uning ikkala qismi ham nolga teng.

Bu nuqtalar o'qni intervallarga ajratadi.

Bu oraliqlarning har birida tengsizligimizning chap tomonidagi kasr-ratsional funksiyaning ishorasini aniqlaylik. Esda tutamizki, kasrli ratsional funktsiya faqat nolga teng yoki mavjud bo'lmagan nuqtalarda belgini o'zgartirishi mumkin. Bu shuni anglatadiki, pay yoki maxraj yo'qolgan nuqtalar orasidagi intervallarning har birida tengsizlikning chap tomonidagi ifoda belgisi doimiy bo'ladi - "ortiqcha" yoki "minus".

Va shuning uchun har bir bunday oraliqda funktsiyaning ishorasini aniqlash uchun biz ushbu intervalga tegishli har qanday nuqtani olamiz. Bizga mos keladigani.
. Masalan, tengsizlikning chap tomonidagi ifoda belgisini oling. "Qavslar" ning har biri salbiy. Chap tomonda belgi bor.

Keyingi interval: . Keling, belgini tekshirib ko'raylik. Biz chap tomonning belgisini o'zgartirganligini tushunamiz.

Keling, olaylik. Ifoda ijobiy bo'lsa - demak, u dan gacha bo'lgan butun intervalda ijobiy bo'ladi.

uchun, tengsizlikning chap tomoni manfiy.

Va nihoyat class="tex" alt="(!LANG:x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Qaysi intervallarda ifoda ijobiy ekanligini aniqladik. Javob yozish qoladi:

Javob: .

Iltimos, diqqat qiling: intervallardagi belgilar bir-birini almashtiradi. Bu sodir bo'ldi, chunki har bir nuqtadan o'tayotganda, chiziqli omillardan biri belgini o'zgartirdi, qolganlari esa uni o'zgarmadi.

Biz interval usuli juda oddiy ekanligini ko'ramiz. Kasr-ratsional tengsizlikni intervallar usuli bilan yechish uchun uni quyidagi shaklga keltiramiz:

Yoki class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle P\left(x \o'ng))(\displaystyle Q\left(x \o'ng)) > 0"> !}, yoki yoki.

(chap tomonda - kasr-ratsional funktsiya, o'ng tomonda - nol).

Keyin - raqam chizig'ida hisoblagich yoki maxraj yo'qolgan nuqtalarni belgilaymiz.
Bu nuqtalar butun son chizig'ini intervallarga ajratadi, ularning har birida kasr-ratsional funktsiya o'z belgisini saqlab qoladi.
Har bir oraliqda uning belgisini bilishgina qoladi.
Buni berilgan oraliqning istalgan nuqtasida ifoda belgisini tekshirish orqali amalga oshiramiz. Shundan so'ng biz javobni yozamiz. Ana xolos.

Ammo savol tug'iladi: belgilar har doim o'zgarib turadimi? Yo'q har doim emas! Biz belgilarni mexanik va o'ylamasdan joylashtirishdan ehtiyot bo'lishimiz kerak.

2. Keling, boshqa tengsizlikni ko'rib chiqaylik.

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle \left(x-2 \o'ng)^2)(\displaystyle \chap(x-1 \o'ng)) \left(x-3\right))>0"> !}

Biz yana nuqtalarni o'qga joylashtiramiz. Nuqtalar va nuqtalar teshilgan, chunki ular maxrajning nollaridir. Tengsizlik qat'iy bo'lgani uchun nuqta ham teshilgan.

Numerator musbat bo'lsa, maxrajdagi ikkala omil ham manfiy bo'ladi. Buni ma'lum bir oraliqdan istalgan raqamni olish orqali tekshirish oson, masalan, . Chap tomonda quyidagi belgi bor:

Numerator musbat bo'lsa; maxrajdagi birinchi omil ijobiy, ikkinchi omil salbiy. Chap tomonda quyidagi belgi bor:

Vaziyat bir xil bo'lganda! Numerator musbat, maxrajdagi birinchi omil ijobiy, ikkinchisi salbiy. Chap tomonda quyidagi belgi bor:

Nihoyat, class="tex" alt="(!LANG:x>3) bilan"> все множители положительны, и левая часть имеет знак :!}

Javob: .

Nima uchun belgilar almashinuvi buzildi? Chunki nuqtadan o'tayotganda multiplikator buning uchun "mas'ul" belgisini o'zgartirmadi. Shunday qilib, tengsizligimizning chap tomoni ham belgini o'zgartirmadi.

Chiqish: agar chiziqli omil teng quvvatda bo'lsa (masalan, kvadratda), u holda nuqtadan o'tayotganda chap tomondagi ifoda belgisi o'zgarmaydi.. G'alati daraja bo'lsa, belgi, albatta, o'zgaradi.

3. Keling, yanada murakkab ishni ko'rib chiqaylik. Bu avvalgisidan farq qiladi, chunki tengsizlik qat'iy emas:

Chap tomoni oldingi muammoda bo'lgani kabi. Belgilarning rasmi bir xil bo'ladi:

Balki javob bir xil bo'lar? Yo'q! Yechim qo'shiladi Buning sababi shundaki, da , tengsizlikning chap va o'ng tomonlari ham nolga teng - shuning uchun bu nuqta yechim hisoblanadi.

Javob: .

Matematikadan imtihondagi masalada bunday holat tez-tez uchrab turadi. Bu yerda abituriyentlar tuzoqqa tushib, ochko yo‘qotishadi. Diqqatli bo'ling!

4. Agar pay yoki maxrajni chiziqli omillarga ajratib bo'lmasa-chi? Ushbu tengsizlikni ko'rib chiqing:

Kvadrat trinomial faktorlarga ajratilmaydi: diskriminant manfiy, ildizlari yo'q. Lekin bu yaxshi! Demak, ifoda belgisi hamma uchun bir xil, xususan, ijobiydir. Bu haqda ko'proq ma'lumotni kvadrat funktsiyaning xususiyatlari haqidagi maqolada o'qishingiz mumkin.

Va endi biz tengsizligimizning ikkala tomonini hamma uchun ijobiy bo'lgan qiymatga bo'lishimiz mumkin. Ekvivalent tengsizlikka erishamiz:

Interval usuli bilan osonlikcha yechiladi.

E'tibor bering - biz tengsizlikning ikkala tomonini ijobiy ekanligini aniq bilgan qiymatga bo'ldik. Albatta, umumiy holatda, tengsizlikni belgisi noma'lum o'zgaruvchiga ko'paytirmaslik yoki bo'lish kerak emas.

5 . Ko'rinishidan juda oddiy bo'lgan boshqa tengsizlikni ko'rib chiqing:

Shuning uchun men uni ga ko'paytirmoqchiman. Ammo biz allaqachon aqllimiz va buni qilmaymiz. Axir, u ham ijobiy, ham salbiy bo'lishi mumkin. Va biz bilamizki, agar tengsizlikning ikkala qismi manfiy qiymatga ko'paytirilsa, tengsizlik belgisi o'zgaradi.

Biz boshqacha harakat qilamiz - biz hamma narsani bir qismga yig'amiz va uni umumiy maxrajga keltiramiz. Nol o'ng tomonda qoladi:

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}

Va bundan keyin - amal qiladi interval usuli.

Tengsizliklarni onlayn hal qilish

Tengsizliklarni yechishdan oldin tenglamalar qanday yechilishini yaxshi tushunish kerak.

Tengsizlik qat'iy () yoki qat'iy emas (≤, ≥) bo'lishidan qat'i nazar, birinchi qadam tengsizlik belgisini tenglik (=) bilan almashtirish orqali tenglamani yechishdir.

Tengsizlikni yechish nimani anglatishini tushuntiring?

Tenglamalarni o'rgangandan so'ng, talabaning boshida quyidagi rasm paydo bo'ladi: siz tenglamaning ikkala qismi bir xil qiymatlarni oladigan o'zgaruvchining shunday qiymatlarini topishingiz kerak. Boshqacha qilib aytganda, tenglik mavjud bo'lgan barcha nuqtalarni toping. Hammasi to'g'ri!

Tengsizliklar haqida gapirganda, ular tengsizlik o'rinli bo'lgan intervallarni (segmentlarni) topishni anglatadi. Agar tengsizlikda ikkita o'zgaruvchi bo'lsa, u holda yechim endi intervallar emas, balki tekislikdagi ba'zi joylar bo'ladi. Tasavvur qiling-a, uchta o'zgaruvchidagi tengsizlikning yechimi qanday bo'ladi?

Tengsizliklarni qanday hal qilish mumkin?

Intervallar usuli (aka intervallar usuli) tengsizliklarni yechishning universal usuli hisoblanadi, u berilgan tengsizlik bajariladigan barcha intervallarni aniqlashdan iborat.

Tengsizlikning turiga kirmasdan, bu holda bu mohiyat emas, mos keladigan tenglamani echish va uning ildizlarini aniqlash, keyin esa bu echimlarni raqamli o'qda belgilash talab qilinadi.

Tengsizlikning yechimini yozishning to‘g‘ri usuli qanday?

Tengsizlikni yechish uchun intervallarni aniqlagandan so'ng, siz yechimning o'zini to'g'ri yozishingiz kerak. Muhim nuance bor - intervallarning chegaralari yechimga kiritilganmi?

Bu erda hamma narsa oddiy. Agar tenglamaning yechimi ODZni qanoatlantirsa va tengsizlik qat’iy bo’lmasa, u holda oraliq chegarasi tengsizlik yechimiga kiradi. Aks holda, yo'q.

Har bir intervalni hisobga olsak, tengsizlikning yechimi oraliqning o'zi yoki yarim interval (uning chegaralaridan biri tengsizlikni qanoatlantirganda) yoki segment - chegaralari bilan birga interval bo'lishi mumkin.

Muhim nuqta

Faqat intervallar, yarim intervallar va segmentlar tengsizlikning yechimi bo'lishi mumkin deb o'ylamang. Yo'q, alohida nuqtalar ham yechimga kiritilishi mumkin.

Masalan, |x|≤0 tengsizlik faqat bitta yechimga ega - 0 nuqta.

Va |x| tengsizligi

Tengsizlik kalkulyatori nima uchun?

Tengsizlik kalkulyatori to'g'ri yakuniy javobni beradi. Bunday holda, ko'p hollarda, raqamli o'q yoki tekislikning tasviri berilgan. Intervallarning chegaralari yechimga kiritilgan yoki yo'qligini ko'rishingiz mumkin - nuqtalar to'ldirilgan yoki teshilgan holda ko'rsatiladi.

Onlayn tengsizlik kalkulyatori tufayli siz tenglamaning ildizlarini to'g'ri topganingizni, ularni raqamlar chizig'ida belgilab qo'yganingizni va intervallar (va chegaralar) bo'yicha tengsizlik shartlarini tekshirganingizni tekshirishingiz mumkinmi?

Agar sizning javobingiz kalkulyatorning javobidan farq qiladigan bo'lsa, unda siz, albatta, yechimingizni ikki marta tekshirishingiz va qilingan xatoni aniqlashingiz kerak.