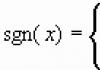Help on Tele2, tariffs, questions

inequality solution in mode online decision almost any given inequality online. Mathematical inequalities online to solve math. Find quickly inequality solution in mode online. The site www.site allows you to find decision almost any given algebraic, trigonometric or transcendent inequality online. When studying almost any section of mathematics at different stages, one has to decide inequalities online. To get an answer immediately, and most importantly an accurate answer, you need a resource that allows you to do this. Thanks to www.site solve inequality online will take a few minutes. The main advantage of www.site when solving mathematical inequalities online- is the speed and accuracy of the issued response. The site is able to solve any algebraic inequalities online, trigonometric inequalities online, transcendental inequalities online, as well as inequalities with unknown parameters in the mode online. inequalities serve as a powerful mathematical apparatus solutions practical tasks. With help mathematical inequalities it is possible to express facts and relations that may at first glance seem confusing and complex. unknown quantities inequalities can be found by formulating the problem in mathematical language in the form inequalities and solve the received task in the mode online on the website www.site. Any algebraic inequality, trigonometric inequality or inequalities containing transcendental features you easily decide online and get the right answer. Studying the natural sciences, one inevitably encounters the need solution of inequalities. In this case, the answer must be accurate and it must be received immediately in the mode online. Therefore, for solve mathematical inequalities online we recommend the site www.site, which will become your indispensable calculator for solve algebraic inequalities online, trigonometric inequalities online, as well as transcendental inequalities online or inequalities with unknown parameters. For practical problems of finding intravol solutions of various mathematical inequalities resource www.. Solving inequalities online yourself, it is useful to check the received answer using online solution of inequalities on the website www.site. It is necessary to write down the inequality correctly and instantly get online solution, after which it remains only to compare the answer with your solution to the inequality. Checking the answer will take no more than a minute, enough solve inequality online and compare answers. This will help you avoid mistakes in decision and correct the answer in time solving inequalities online whether algebraic, trigonometric, transcendent or inequality with unknown parameters.

For example, the expression \(x>5\) is an inequality.

Types of inequalities:

If \(a\) and \(b\) are numbers or , then the inequality is called numerical. In fact, this is just a comparison of two numbers. These inequalities are subdivided into faithful and unfaithful.

For example:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);

\(17+3\geq 115\) is an invalid numerical inequality because \(17+3=20\) and \(20\) is less than \(115\) (not greater than or equal to).

If \(a\) and \(b\) are expressions containing a variable, then we have inequality with variable. Such inequalities are divided into types depending on the content:

What is a solution to an inequality?

If any number is substituted into the inequality instead of a variable, then it will turn into a numeric one.

If the given value for x makes the original inequality true numerical, then it is called solving the inequality. If not, then this value is not a solution. And to solve inequality- you need to find all its solutions (or show that they do not exist).

For example, if we are in the linear inequality \(x+6>10\), we substitute the number \(7\) instead of x, we get the correct numerical inequality: \(13>10\). And if we substitute \(2\), there will be an incorrect numerical inequality \(8>10\). That is, \(7\) is a solution to the original inequality, but \(2\) is not.

However, the inequality \(x+6>10\) has other solutions. Indeed, we will get the correct numerical inequalities when substituting and \(5\), and \(12\), and \(138\) ... And how can we find all possible solutions? To do this, use For our case, we have:

\(x+6>10\) \(|-6\)
\(x>4\)

That is, we can use any number greater than four. Now we need to write down the answer. Solutions to inequalities, as a rule, are written numerically, additionally marking them on the numerical axis with hatching. For our case we have:

Answer: \(x\in(4;+\infty)\)

When does the sign change in an inequality?

There is one big trap in inequalities, which students really “like” to fall into:

When multiplying (or dividing) inequality by a negative number, it is reversed (“greater than” by “less”, “greater than or equal to” by “less than or equal to”, and so on)

Why is this happening? To understand this, let's look at the transformations of the numerical inequality \(3>1\). It is correct, the triple is really more than one. First, let's try to multiply it by any positive number, for example, two:

\(3>1\) \(|\cdot2\)
\(6>2\)

As you can see, after multiplication, the inequality remains true. And no matter what positive number we multiply, we will always get the correct inequality. And now let's try to multiply by a negative number, for example, minus three:

\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)

It turned out to be an incorrect inequality, because minus nine is less than minus three! That is, in order for the inequality to become true (which means that the transformation of multiplication by a negative was “legal”), you need to flip the comparison sign, like this: \(−9<− 3\).
With division, it will turn out similarly, you can check it yourself.

The rule written above applies to all types of inequalities, and not just to numerical ones.

Answer: \(x\in(-1;\infty)\)

Inequalities and DHS

Inequalities, as well as equations, can have restrictions on , that is, on the values ​​of x. Accordingly, those values ​​that are unacceptable according to the ODZ should be excluded from the solution interval.

Example: Solve the inequality \(\sqrt(x+1)<3\)

Decision: It is clear that in order for the left side to be less than \(3\), the root expression must be less than \(9\) (after all, from \(9\) just \(3\)). We get:

\(x+1<9\) \(|-1\)
\(x<8\)

Everybody? Any value of x less than \(8\) will suit us? No! Because if we take, for example, the value \(-5\) that seems to fit the requirement, it will not be a solution to the original inequality, since it will lead us to calculating the root of a negative number.

\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)

Therefore, we must also take into account the restrictions on the values ​​​​of x - it cannot be such that there is a negative number under the root. Thus, we have the second requirement for x:

\(x+1\geq0\)
\(x\geq-1\)

And for x to be a final solution, it must satisfy both requirements at once: it must be less than \(8\) (to be a solution) and greater than \(-1\) (to be valid in principle). Plotting on the number line, we have the final answer:

Answer: \(\left[-1;8\right)\)

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

What's happened "square inequality"? Not a question!) If you take any quadratic equation and change the sign in it "=" (equal) to any inequality icon ( > ≥ < ≤ ≠ ), we get a quadratic inequality. For example:

1. x2 -8x+12 ≥ 0

2. -x 2 +3x > 0

3. x2 ≤ 4

Well, you get the idea...)

I knowingly linked equations and inequalities here. The fact is that the first step in solving any square inequality - solve the equation from which this inequality is made. For this reason - the inability to solve quadratic equations automatically leads to a complete failure in inequalities. Is the hint clear?) If anything, look at how to solve any quadratic equations. Everything is detailed there. And in this lesson we will deal with inequalities.

The inequality ready for solution has the form: left - square trinomial ax 2 +bx+c, on the right - zero. The inequality sign can be absolutely anything. The first two examples are here are ready for a decision. The third example still needs to be prepared.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

Today, friends, there will be no snot and sentiment. Instead, I will send you into battle with one of the most formidable opponents in the 8th-9th grade algebra course without further questions.

Yes, you understood everything correctly: we are talking about inequalities with a modulus. We will look at four basic techniques with which you will learn to solve about 90% of these problems. What about the other 10%? Well, we'll talk about them in a separate lesson. :)

However, before analyzing any tricks there, I would like to recall two facts that you already need to know. Otherwise, you risk not understanding the material of today's lesson at all.

What you already need to know

Captain Evidence, as it were, hints that in order to solve inequalities with a modulus, you need to know two things:

1. How are inequalities resolved?
2. What is a module.

Let's start with the second point.

Module Definition

Everything is simple here. There are two definitions: algebraic and graphic. Let's start with the algebra:

Definition. The module of the number $x$ is either the number itself, if it is non-negative, or the number opposite to it, if the original $x$ is still negative.

It is written like this:

\[\left| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]

In simple terms, the modulus is “a number without a minus”. And it is in this duality (somewhere you don’t need to do anything with the original number, but somewhere you have to remove some minus there) and all the difficulty for novice students lies.

There is also a geometric definition. It is also useful to know it, but we will refer to it only in complex and some special cases, where the geometric approach is more convenient than the algebraic one (spoiler: not today).

Definition. Let the point $a$ be marked on the real line. Then the module $\left| x-a \right|$ is the distance from the point $x$ to the point $a$ on this line.

If you draw a picture, you get something like this:

One way or another, its key property immediately follows from the definition of the module: the modulus of a number is always a non-negative value. This fact will be a red thread running through our entire story today.

Solution of inequalities. Spacing Method

Now let's deal with inequalities. There are a great many of them, but our task now is to be able to solve at least the simplest of them. Those that are reduced to linear inequalities, as well as to the method of intervals.

I have two big tutorials on this topic (by the way, very, VERY useful - I recommend studying):

1. The interval method for inequalities (especially watch the video);
2. Fractional-rational inequalities is a very voluminous lesson, but after it you will not have any questions left at all.

If you know all this, if the phrase "let's move from inequality to equation" does not make you vaguely want to kill yourself against the wall, then you are ready: welcome to hell to the main topic of the lesson. :)

1. Inequalities of the form "Module less than function"

This is one of the most frequently encountered tasks with modules. It is required to solve an inequality of the form:

\[\left| f\right| \ltg\]

Anything can act as functions $f$ and $g$, but usually they are polynomials. Examples of such inequalities:

\[\begin(align) & \left| 2x+3\right| \ltx+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\left| x \right|-3 \right| \lt 2. \\\end(align)\]

All of them are solved literally in one line according to the scheme:

\[\left| f\right| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \right.\right)\]

It is easy to see that we get rid of the module, but instead we get a double inequality (or, which is the same thing, a system of two inequalities). But this transition takes into account absolutely all possible problems: if the number under the module is positive, the method works; if negative, it still works; and even with the most inadequate function in place of $f$ or $g$, the method will still work.

Naturally, the question arises: is it not easier? Unfortunately, you can't. This is the whole point of the module.

But enough of the philosophizing. Let's solve a couple of problems:

A task. Solve the inequality:

\[\left| 2x+3\right| \ltx+7\]

Decision. So, we have a classical inequality of the form “the module is less than” - there is even nothing to transform. We work according to the algorithm:

\[\begin(align) & \left| f\right| \lt g\Rightarrow -g \lt f \lt g; \\ & \left| 2x+3\right| \lt x+7\Rightarrow -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Do not rush to open the brackets that are preceded by a “minus”: it is quite possible that because of the haste you will make an offensive mistake.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

The problem has been reduced to two elementary inequalities. We note their solutions on parallel real lines:

Intersection of many

The intersection of these sets will be the answer.

Answer: $x\in \left(-\frac(10)(3);4 \right)$

A task. Solve the inequality:

\[\left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Decision. This task is a little more difficult. To begin with, we isolate the module by moving the second term to the right:

\[\left| ((x)^(2))+2x-3 \right| \lt -3\left(x+1 \right)\]

Obviously, we again have an inequality of the form “the module is less”, so we get rid of the module according to the already known algorithm:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Now attention: someone will say that I'm a bit of a pervert with all these brackets. But once again I remind you that our key goal is correctly solve the inequality and get the answer. Later, when you have perfectly mastered everything that is described in this lesson, you can pervert yourself as you like: open brackets, add minuses, etc.

And for starters, we just get rid of the double minus on the left:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\left(x+1\right)\]

Now let's open all the brackets in the double inequality:

Let's move on to double inequality. This time the calculations will be more serious:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( align)\right.\]

Both inequalities are square and are solved by the interval method (that's why I say: if you don't know what it is, it's better not to take on modules yet). We pass to the equation in the first inequality:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(align)\]

As you can see, the output turned out to be an incomplete quadratic equation, which is solved elementarily. Now let's deal with the second inequality of the system. There you have to apply Vieta's theorem:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(align)\]

We mark the obtained numbers on two parallel lines (separate for the first inequality and separate for the second):

Again, since we are solving a system of inequalities, we are interested in the intersection of the shaded sets: $x\in \left(-5;-2 \right)$. This is the answer.

Answer: $x\in \left(-5;-2 \right)$

I think after these examples the solution scheme is very clear:

1. Isolate the module by moving all other terms to the opposite side of the inequality. Thus we get an inequality of the form $\left| f\right| \ltg$.
2. Solve this inequality by getting rid of the module as described above. At some point, it will be necessary to move from a double inequality to a system of two independent expressions, each of which can already be solved separately.
3. Finally, it remains only to cross the solutions of these two independent expressions - and that's it, we will get the final answer.

A similar algorithm exists for inequalities of the following type, when the modulus is greater than the function. However, there are a couple of serious "buts". We will talk about these “buts” now.

2. Inequalities of the form "Module is greater than function"

They look like this:

\[\left| f\right| \gt g\]

Similar to the previous one? It seems. Nevertheless, such tasks are solved in a completely different way. Formally, the scheme is as follows:

\[\left| f\right| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

In other words, we consider two cases:

1. First, we simply ignore the module - we solve the usual inequality;
2. Then, in fact, we open the module with the minus sign, and then we multiply both parts of the inequality by −1, with a sign.

In this case, the options are combined with a square bracket, i.e. We have a combination of two requirements.

Pay attention again: before us is not a system, but an aggregate, therefore in the answer, the sets are combined, not intersected. This is a fundamental difference from the previous paragraph!

In general, many students have a lot of confusion with unions and intersections, so let's look into this issue once and for all:

• "∪" is a concatenation sign. In fact, this is a stylized letter "U", which came to us from the English language and is an abbreviation for "Union", i.e. "Associations".
• "∩" is the intersection sign. This crap didn't come from anywhere, but just appeared as an opposition to "∪".

To make it even easier to remember, just add legs to these signs to make glasses (just don’t accuse me of promoting drug addiction and alcoholism now: if you are seriously studying this lesson, then you are already a drug addict):

Translated into Russian, this means the following: the union (collection) includes elements from both sets, therefore, no less than each of them; but the intersection (system) includes only those elements that are both in the first set and in the second. Therefore, the intersection of sets is never greater than the source sets.

So it became clearer? That is great. Let's move on to practice.

A task. Solve the inequality:

\[\left| 3x+1 \right| \gt 5-4x\]

Decision. We act according to the scheme:

\[\left| 3x+1 \right| \gt 5-4x\Rightarrow \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ right.\]

We solve each population inequality:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

We mark each resulting set on the number line, and then combine them:

Union of sets

Obviously the answer is $x\in \left(\frac(4)(7);+\infty \right)$

Answer: $x\in \left(\frac(4)(7);+\infty \right)$

A task. Solve the inequality:

\[\left| ((x)^(2))+2x-3 \right| \gtx\]

Decision. Well? No, it's all the same. We pass from an inequality with a modulus to a set of two inequalities:

\[\left| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]

We solve each inequality. Unfortunately, the roots will not be very good there:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(align)\]

In the second inequality, there is also a bit of game:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(align)\]

Now we need to mark these numbers on two axes - one axis for each inequality. However, you need to mark the points in the correct order: the larger the number, the further the point shifts to the right.

And here we are waiting for a setup. If everything is clear with the numbers $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (the terms in the numerator of the first fraction are less than the terms in the numerator of the second , so the sum is also smaller), with the numbers $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt(21))(2)$ there will also be no difficulty (a positive number obviously more negative), but with the last couple, everything is not so simple. Which is larger: $\frac(-3+\sqrt(21))(2)$ or $\frac(-1+\sqrt(13))(2)$? The arrangement of points on the number lines and, in fact, the answer will depend on the answer to this question.

So let's compare:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

We isolated the root, got non-negative numbers on both sides of the inequality, so we have the right to square both sides:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

I think it's a no brainer that $4\sqrt(13) \gt 3$, so $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) (2)$, finally the points on the axes will be arranged like this:

Case of ugly roots

Let me remind you that we are solving a set, so the answer will be the union, and not the intersection of the shaded sets.

Answer: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

As you can see, our scheme works great both for simple tasks and for very hard ones. The only “weak spot” in this approach is that you need to correctly compare irrational numbers (and believe me: these are not only roots). But a separate (and very serious lesson) will be devoted to questions of comparison. And we move on.

3. Inequalities with non-negative "tails"

So we got to the most interesting. These are inequalities of the form:

\[\left| f\right| \gt\left| g\right|\]

Generally speaking, the algorithm that we are going to talk about now is true only for the module. It works in all inequalities where there are guaranteed non-negative expressions on the left and right:

What to do with these tasks? Just remember:

In inequalities with non-negative tails, both sides can be raised to any natural power. There will be no additional restrictions.

First of all, we will be interested in squaring - it burns modules and roots:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\end(align)\]

Just do not confuse this with taking the root of the square:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Countless mistakes were made when a student forgot to install a module! But this is a completely different story (these are, as it were, irrational equations), so we will not go into it now. Let's better solve a couple of problems:

A task. Solve the inequality:

\[\left| x+2 \right|\ge \left| 1-2x \right|\]

Decision. We immediately notice two things:

1. This is a non-strict inequality. Points on the number line will be punched out.
2. Both sides of the inequality are obviously non-negative (this is a property of the module: $\left| f\left(x \right) \right|\ge 0$).

Therefore, we can square both sides of the inequality to get rid of the modulus and solve the problem using the usual interval method:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\end(align)\]

At the last step, I cheated a little: I changed the sequence of terms, using the parity of the modulus (in fact, I multiplied the expression $1-2x$ by −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ right)\right)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

We solve by the interval method. Let's move from inequality to equation:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(align)\]

We mark the found roots on the number line. Once again: all points are shaded because the original inequality is not strict!

Getting rid of the module sign

Let me remind you for the especially stubborn: we take the signs from the last inequality, which was written down before moving on to the equation. And we paint over the areas required in the same inequality. In our case, this is $\left(x-3 \right)\left(3x+1 \right)\le 0$.

That's it. Problem solved.

Answer: $x\in \left[ -\frac(1)(3);3 \right]$.

A task. Solve the inequality:

\[\left| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]

Decision. We do everything the same. I will not comment - just look at the sequence of actions.

Let's square it:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ right))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Spacing method:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Rightarrow x=-1.5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varnothing . \\\end(align)\]

There is only one root on the number line:

The answer is a whole range

Answer: $x\in \left[ -1.5;+\infty \right)$.

A small note about the last task. As one of my students accurately noted, both submodule expressions in this inequality are obviously positive, so the modulus sign can be omitted without harm to health.

But this is already a completely different level of thinking and a different approach - it can be conditionally called the method of consequences. About him - in a separate lesson. And now let's move on to the final part of today's lesson and consider a universal algorithm that always works. Even when all previous approaches were powerless. :)

4. Method of enumeration of options

What if all these tricks don't work? If the inequality does not reduce to non-negative tails, if it is impossible to isolate the module, if at all pain-sadness-longing?

Then the “heavy artillery” of all mathematics enters the scene - the enumeration method. With regard to inequalities with the modulus, it looks like this:

1. Write out all submodule expressions and equate them to zero;
2. Solve the resulting equations and mark the found roots on one number line;
3. The straight line will be divided into several sections, within which each module has a fixed sign and therefore unambiguously expands;
4. Solve the inequality on each such section (you can separately consider the boundary roots obtained in paragraph 2 - for reliability). Combine the results - this will be the answer. :)

Well, how? Weak? Easy! Only for a long time. Let's see in practice:

A task. Solve the inequality:

\[\left| x+2 \right| \lt\left| x-1 \right|+x-\frac(3)(2)\]

Decision. This crap doesn't boil down to inequalities like $\left| f\right| \lt g$, $\left| f\right| \gt g$ or $\left| f\right| \lt\left| g \right|$, so let's go ahead.

We write out submodule expressions, equate them to zero and find the roots:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Rightarrow x=1. \\\end(align)\]

In total, we have two roots that divide the number line into three sections, inside which each module is revealed uniquely:

Splitting the number line by zeros of submodular functions

Let's consider each section separately.

1. Let $x \lt -2$. Then both submodule expressions are negative, and the original inequality is rewritten as follows:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end(align)\]

We got a fairly simple constraint. Let's intersect it with the original assumption that $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Obviously, the variable $x$ cannot simultaneously be less than −2 but greater than 1.5. There are no solutions in this area.

1.1. Let's separately consider the boundary case: $x=-2$. Let's just substitute this number into the original inequality and check: does it hold?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \right|-2-1.5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0,5\Rightarrow \varnothing . \\\end(align)\]

Obviously, the chain of calculations has led us to the wrong inequality. Therefore, the original inequality is also false, and $x=-2$ is not included in the answer.

2. Now let $-2 \lt x \lt 1$. The left module will already open with a "plus", but the right one is still with a "minus". We have:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt -2.5 \\\end(align)\]

Again we intersect with the original requirement:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

And again, the empty set of solutions, since there are no numbers that are both less than −2.5 and greater than −2.

2.1. And again a special case: $x=1$. We substitute into the original inequality:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \left| 3\right| \lt\left| 0 \right|+1-1.5; \\ & 3 \lt -0.5; \\ & 3 \lt -0,5\Rightarrow \varnothing . \\\end(align)\]

Similarly to the previous "special case", the number $x=1$ is clearly not included in the answer.

3. The last piece of the line: $x \gt 1$. Here all modules are expanded with a plus sign:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\]

And again we intersect the found set with the original constraint:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \right)\]

Finally! We have found the interval, which will be the answer.

Answer: $x\in \left(4,5;+\infty \right)$

Finally, one note that may save you from stupid mistakes when solving real problems:

Solutions of inequalities with modules are usually continuous sets on the number line - intervals and segments. Isolated points are much rarer. And even more rarely, it happens that the boundaries of the solution (the end of the segment) coincide with the boundary of the range under consideration.

Therefore, if the boundaries (those very “special cases”) are not included in the answer, then the areas to the left-right of these boundaries will almost certainly not be included in the answer either. And vice versa: the border entered in response, which means that some areas around it will also be responses.

Keep this in mind when you check your solutions.

First, some lyrics to get a feel for the problem that the interval method solves. Suppose we need to solve the following inequality:

(x − 5)(x + 3) > 0

What are the options? The first thing that comes to mind for most students is the rules "plus times plus makes plus" and "minus times minus makes plus." Therefore, it suffices to consider the case when both brackets are positive: x − 5 > 0 and x + 3 > 0. Then we also consider the case when both brackets are negative: x − 5< 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:

More advanced students will remember (perhaps) that on the left is a quadratic function whose graph is a parabola. Moreover, this parabola intersects the OX axis at the points x = 5 and x = −3. For further work, you need to open the brackets. We have:

x 2 − 2x − 15 > 0

Now it is clear that the branches of the parabola are directed upwards, because coefficient a = 1 > 0. Let's try to draw a diagram of this parabola:

The function is greater than zero where it passes above the OX axis. In our case, these are the intervals (−∞ −3) and (5; +∞) - this is the answer.

Please note that the picture shows exactly function diagram, not her schedule. Because for a real graph, you need to calculate coordinates, calculate offsets and other crap, which we don’t need at all now.

Why are these methods ineffective?

So, we have considered two solutions to the same inequality. Both of them turned out to be very cumbersome. The first decision arises - just think about it! is a set of systems of inequalities. The second solution is also not very easy: you need to remember the parabola graph and a bunch of other small facts.

It was a very simple inequality. It has only 2 multipliers. Now imagine that there will be not 2 multipliers, but at least 4. For example:

(x − 7)(x − 1)(x + 4)(x + 9)< 0

How to solve such inequality? Go through all possible combinations of pros and cons? Yes, we will fall asleep faster than we find a solution. Drawing a graph is also not an option, since it is not clear how such a function behaves on the coordinate plane.

For such inequalities, a special solution algorithm is needed, which we will consider today.

What is the interval method

The interval method is a special algorithm designed to solve complex inequalities of the form f (x) > 0 and f (x)< 0. Алгоритм состоит из 4 шагов:

1. Solve the equation f (x) \u003d 0. Thus, instead of an inequality, we get an equation that is much easier to solve;
2. Mark all the obtained roots on the coordinate line. Thus, the straight line will be divided into several intervals;
3. Find out the sign (plus or minus) of the function f (x) on the rightmost interval. To do this, it is enough to substitute in f (x) any number that will be to the right of all the marked roots;
4. Mark marks on other intervals. To do this, it is enough to remember that when passing through each root, the sign changes.

That's all! After that, it remains only to write out the intervals that interest us. They are marked with a “+” sign if the inequality was of the form f (x) > 0, or a “−” sign if the inequality was of the form f (x)< 0.

At first glance, it may seem that the interval method is some kind of tin. But in practice, everything will be very simple. It takes a little practice - and everything will become clear. Take a look at the examples and see for yourself:

A task. Solve the inequality:

(x − 2)(x + 7)< 0

We work on the method of intervals. Step 1: Replace the inequality with an equation and solve it:

(x − 2)(x + 7) = 0

The product is equal to zero if and only if at least one of the factors is equal to zero:

x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.

Got two roots. Go to step 2: mark these roots on the coordinate line. We have:

Now step 3: we find the sign of the function on the rightmost interval (to the right of the marked point x = 2). To do this, you need to take any number that is greater than the number x = 2. For example, let's take x = 3 (but no one forbids taking x = 4, x = 10, and even x = 10,000). We get:

f(x) = (x − 2)(x + 7);
x=3;
f (3) = (3 − 2)(3 + 7) = 1 10 = 10;

We get that f (3) = 10 > 0, so we put a plus sign in the rightmost interval.

We pass to the last point - it is necessary to note the signs on the remaining intervals. Remember that when passing through each root, the sign must change. For example, to the right of the root x = 2 there is a plus (we made sure of this in the previous step), so there must be a minus on the left.

This minus extends to the entire interval (−7; 2), so there is a minus to the right of the root x = −7. Therefore, there is a plus to the left of the root x = −7. It remains to mark these signs on the coordinate axis. We have:

Let's return to the original inequality, which looked like:

(x − 2)(x + 7)< 0

So the function must be less than zero. This means that we are interested in the minus sign, which occurs only on one interval: (−7; 2). This will be the answer.

A task. Solve the inequality:

(x + 9)(x − 3)(1 − x )< 0

Step 1: Equate the left side to zero:

(x + 9)(x − 3)(1 − x ) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.

Remember: the product is zero when at least one of the factors is zero. That is why we have the right to equate to zero each individual bracket.

Step 2: mark all the roots on the coordinate line:

Step 3: find out the sign of the rightmost gap. We take any number that is greater than x = 1. For example, we can take x = 10. We have:

f (x) \u003d (x + 9) (x - 3) (1 - x);
x=10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 7 (−9) = − 1197;
f(10) = -1197< 0.

Step 4: Place the rest of the signs. Remember that when passing through each root, the sign changes. As a result, our picture will look like this:

That's all. It remains only to write the answer. Take another look at the original inequality:

(x + 9)(x − 3)(1 − x )< 0

This is an inequality of the form f (x)< 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:

x ∈ (−9; 1) ∪ (3; +∞)

This is the answer.

A note about function signs

Practice shows that the greatest difficulties in the interval method arise at the last two steps, i.e. when placing signs. Many students begin to get confused: what numbers to take and where to put signs.

To finally understand the interval method, consider two remarks on which it is built:

1. A continuous function changes sign only at the points where it is equal to zero. Such points break the coordinate axis into pieces, within which the sign of the function never changes. That's why we solve the equation f (x) \u003d 0 and mark the found roots on a straight line. The numbers found are the "boundary" points separating the pluses from the minuses.
2. To find out the sign of a function on any interval, it is enough to substitute any number from this interval into the function. For example, for the interval (−5; 6) we can take x = −4, x = 0, x = 4 and even x = 1.29374 if we want. Why is it important? Yes, because many students begin to gnaw doubts. Like, what if for x = −4 we get a plus, and for x = 0 we get a minus? Nothing like that will ever happen. All points in the same interval give the same sign. Remember this.

That's all you need to know about the interval method. Of course, we have dismantled it in its simplest form. There are more complex inequalities - non-strict, fractional and with repeated roots. For them, you can also apply the interval method, but this is a topic for a separate large lesson.

Now I would like to analyze an advanced trick that drastically simplifies the interval method. More precisely, the simplification affects only the third step - the calculation of the sign on the rightmost piece of the line. For some reason, this technique is not held in schools (at least no one explained this to me). But in vain - in fact, this algorithm is very simple.

So, the sign of the function is on the right piece of the numerical axis. This piece has the form (a; +∞), where a is the largest root of the equation f (x) = 0. In order not to blow our brains, consider a specific example:

(x − 1)(2 + x )(7 − x )< 0;
f (x) \u003d (x - 1) (2 + x) (7 - x);
(x − 1)(2 + x )(7 − x ) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

We got 3 roots. We list them in ascending order: x = −2, x = 1 and x = 7. Obviously, the largest root is x = 7.

For those who find it easier to reason graphically, I will mark these roots on the coordinate line. Let's see what happens:

It is required to find the sign of the function f (x) on the rightmost interval, i.e. on (7; +∞). But as we have already noted, to determine the sign, you can take any number from this interval. For example, you can take x = 8, x = 150, etc. And now - the same technique that is not taught in schools: let's take infinity as a number. More precisely, plus infinity, i.e. +∞.

"Are you stoned? How can you substitute infinity into a function? perhaps, you ask. But think about it: we do not need the value of the function itself, we only need the sign. Therefore, for example, the values ​​f (x) = −1 and f (x) = −938 740 576 215 mean the same thing: the function is negative on this interval. Therefore, all that is required of you is to find the sign that occurs at infinity, and not the value of the function.

In fact, substituting infinity is very simple. Let's go back to our function:

f(x) = (x − 1)(2 + x)(7 − x)

Imagine that x is a very large number. A billion or even a trillion. Now let's see what happens in each parenthesis.

First bracket: (x − 1). What happens if you subtract one from a billion? The result will be a number not much different from a billion, and this number will be positive. Similarly with the second bracket: (2 + x). If we add a billion to two, we get a billion with kopecks - this is a positive number. Finally, the third bracket: (7 − x ). Here there will be minus a billion, from which a miserable piece in the form of a seven has been “gnawed off”. Those. the resulting number will not differ much from minus a billion - it will be negative.

It remains to find the sign of the whole work. Since we had a plus in the first brackets, and a minus in the last bracket, we get the following construction:

(+) · (+) · (−) = (−)

The final sign is minus! It doesn't matter what the value of the function itself is. The main thing is that this value is negative, i.e. on the rightmost interval there is a minus sign. It remains to complete the fourth step of the interval method: arrange all the signs. We have:

The original inequality looked like:

(x − 1)(2 + x )(7 − x )< 0

Therefore, we are interested in the intervals marked with a minus sign. We write out the answer:

x ∈ (−2; 1) ∪ (7; +∞)

That's the whole trick that I wanted to tell. In conclusion, there is one more inequality, which is solved by the interval method using infinity. To visually shorten the solution, I will not write step numbers and detailed comments. I will write only what really needs to be written when solving real problems:

A task. Solve the inequality:

x (2x + 8)(x − 3) > 0

We replace the inequality with an equation and solve it:

x (2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

We mark all three roots on the coordinate line (immediately with signs):

There is a plus on the right side of the coordinate axis, because the function looks like:

f(x) = x(2x + 8)(x − 3)

And if we substitute infinity (for example, a billion), we get three positive brackets. Since the original expression must be greater than zero, we are only interested in pluses. It remains to write the answer:

x ∈ (−4; 0) ∪ (3; +∞)