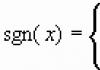Solution of inequalities. Available on how to solve inequalities

Today, friends, there will be no snot and sentiment. Instead, I will send you into battle with one of the most formidable opponents in the 8th-9th grade algebra course without further questions.

Yes, you understood everything correctly: we are talking about inequalities with a modulus. We will look at four basic techniques with which you will learn to solve about 90% of these problems. What about the other 10%? Well, we'll talk about them in a separate lesson. :)

However, before analyzing any tricks there, I would like to recall two facts that you already need to know. Otherwise, you risk not understanding the material of today's lesson at all.

What you already need to know

Captain Evidence, as it were, hints that in order to solve inequalities with a modulus, you need to know two things:

How are inequalities resolved?
What is a module.

Let's start with the second point.

Module Definition

Everything is simple here. There are two definitions: algebraic and graphic. Let's start with the algebra:

Definition. The module of the number $x$ is either the number itself, if it is non-negative, or the number opposite to it, if the original $x$ is still negative.

It is written like this:

\[\left| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]

In simple terms, the modulus is “a number without a minus”. And it is in this duality (somewhere you don’t need to do anything with the original number, but somewhere you have to remove some minus there) and all the difficulty for novice students lies.

There is also a geometric definition. It is also useful to know it, but we will refer to it only in complex and some special cases, where the geometric approach is more convenient than the algebraic one (spoiler: not today).

Definition. Let the point $a$ be marked on the real line. Then the module $\left| x-a \right|$ is the distance from the point $x$ to the point $a$ on this line.

If you draw a picture, you get something like this:

Graphical module definition

One way or another, its key property immediately follows from the definition of the module: the modulus of a number is always a non-negative value. This fact will be a red thread running through our entire story today.

Solution of inequalities. Spacing Method

Now let's deal with inequalities. There are a great many of them, but our task now is to be able to solve at least the simplest of them. Those that are reduced to linear inequalities, as well as to the method of intervals.

I have two big tutorials on this topic (by the way, very, VERY useful - I recommend studying):

The interval method for inequalities (especially watch the video);
Fractional-rational inequalities is a very voluminous lesson, but after it you will not have any questions left at all.

If you know all this, if the phrase "let's move from inequality to equation" does not make you vaguely want to kill yourself against the wall, then you are ready: welcome to hell to the main topic of the lesson. :)

1. Inequalities of the form "Module less than function"

This is one of the most frequently encountered tasks with modules. It is required to solve an inequality of the form:

\[\left| f\right| \ltg\]

Anything can act as functions $f$ and $g$, but usually they are polynomials. Examples of such inequalities:

All of them are solved literally in one line according to the scheme:

\[\left| f\right| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \right.\right)\]

It is easy to see that we get rid of the module, but instead we get a double inequality (or, which is the same thing, a system of two inequalities). But this transition takes into account absolutely all possible problems: if the number under the module is positive, the method works; if negative, it still works; and even with the most inadequate function in place of $f$ or $g$, the method will still work.

Naturally, the question arises: is it not easier? Unfortunately, you can't. This is the whole point of the module.

But enough of the philosophizing. Let's solve a couple of problems:

A task. Solve the inequality:

\[\left| 2x+3\right| \ltx+7\]

Decision. So, we have a classical inequality of the form “the module is less than” - there is even nothing to transform. We work according to the algorithm:

\[\begin(align) & \left| f\right| \lt g\Rightarrow -g \lt f \lt g; \\ & \left| 2x+3\right| \lt x+7\Rightarrow -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Do not rush to open the brackets that are preceded by a “minus”: it is quite possible that because of the haste you will make an offensive mistake.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

The problem has been reduced to two elementary inequalities. We note their solutions on parallel real lines:
Intersection of many
The intersection of these sets will be the answer.

Answer: $x\in \left(-\frac(10)(3);4 \right)$

A task. Solve the inequality:

\[\left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Decision. This task is a little more difficult. To begin with, we isolate the module by moving the second term to the right:

\[\left| ((x)^(2))+2x-3 \right| \lt -3\left(x+1 \right)\]

Obviously, we again have an inequality of the form “the module is less”, so we get rid of the module according to the already known algorithm:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Now attention: someone will say that I'm a bit of a pervert with all these brackets. But once again I remind you that our key goal is correctly solve the inequality and get the answer. Later, when you have perfectly mastered everything that is described in this lesson, you can pervert yourself as you like: open brackets, add minuses, etc.

And for starters, we just get rid of the double minus on the left:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\left(x+1\right)\]

Now let's open all the brackets in the double inequality:

Let's move on to double inequality. This time the calculations will be more serious:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( align)\right.\]

Both inequalities are square and are solved by the interval method (that's why I say: if you don't know what it is, it's better not to take on modules yet). We pass to the equation in the first inequality:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(align)\]

As you can see, the output turned out to be an incomplete quadratic equation, which is solved elementarily. Now let's deal with the second inequality of the system. There you have to apply Vieta's theorem:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(align)\]

We mark the obtained numbers on two parallel lines (separate for the first inequality and separate for the second):
Again, since we are solving a system of inequalities, we are interested in the intersection of the shaded sets: $x\in \left(-5;-2 \right)$. This is the answer.
Answer: $x\in \left(-5;-2 \right)$

I think after these examples the solution scheme is very clear:

Isolate the module by moving all other terms to the opposite side of the inequality. Thus we get an inequality of the form $\left| f\right| \ltg$.
Solve this inequality by getting rid of the module as described above. At some point, it will be necessary to move from a double inequality to a system of two independent expressions, each of which can already be solved separately.
Finally, it remains only to cross the solutions of these two independent expressions - and that's it, we will get the final answer.

A similar algorithm exists for inequalities of the following type, when the modulus is greater than the function. However, there are a couple of serious "buts". We will talk about these “buts” now.

2. Inequalities of the form "Module is greater than function"

They look like this:

\[\left| f\right| \gt g\]

Similar to the previous one? It seems. Nevertheless, such tasks are solved in a completely different way. Formally, the scheme is as follows:

\[\left| f\right| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

In other words, we consider two cases:

First, we simply ignore the module - we solve the usual inequality;
Then, in fact, we open the module with the minus sign, and then we multiply both parts of the inequality by −1, with a sign.

In this case, the options are combined with a square bracket, i.e. We have a combination of two requirements.

Pay attention again: before us is not a system, but an aggregate, therefore in the answer, the sets are combined, not intersected. This is a fundamental difference from the previous paragraph!

In general, many students have a lot of confusion with unions and intersections, so let's look into this issue once and for all:

"∪" is a concatenation sign. In fact, this is a stylized letter "U", which came to us from the English language and is an abbreviation for "Union", i.e. "Associations".
"∩" is the intersection sign. This crap didn't come from anywhere, but just appeared as an opposition to "∪".

To make it even easier to remember, just add legs to these signs to make glasses (just don’t accuse me of promoting drug addiction and alcoholism now: if you are seriously studying this lesson, then you are already a drug addict):

Difference between intersection and union of sets

Translated into Russian, this means the following: the union (collection) includes elements from both sets, therefore, no less than each of them; but the intersection (system) includes only those elements that are both in the first set and in the second. Therefore, the intersection of sets is never greater than the source sets.

So it became clearer? That is great. Let's move on to practice.

A task. Solve the inequality:

\[\left| 3x+1 \right| \gt 5-4x\]

Decision. We act according to the scheme:

\[\left| 3x+1 \right| \gt 5-4x\Rightarrow \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ right.\]

We solve each population inequality:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

We mark each resulting set on the number line, and then combine them:
Union of sets
Obviously the answer is $x\in \left(\frac(4)(7);+\infty \right)$

Answer: $x\in \left(\frac(4)(7);+\infty \right)$

A task. Solve the inequality:

\[\left| ((x)^(2))+2x-3 \right| \gtx\]

Decision. Well? No, it's all the same. We pass from an inequality with a modulus to a set of two inequalities:

\[\left| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]

We solve each inequality. Unfortunately, the roots will not be very good there:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(align)\]

In the second inequality, there is also a bit of game:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(align)\]

Now we need to mark these numbers on two axes - one axis for each inequality. However, you need to mark the points in the correct order: the larger the number, the further the point shifts to the right.

And here we are waiting for a setup. If everything is clear with the numbers $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (the terms in the numerator of the first fraction are less than the terms in the numerator of the second , so the sum is also smaller), with the numbers $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt(21))(2)$ there will also be no difficulty (a positive number obviously more negative), but with the last couple, everything is not so simple. Which is larger: $\frac(-3+\sqrt(21))(2)$ or $\frac(-1+\sqrt(13))(2)$? The arrangement of points on the number lines and, in fact, the answer will depend on the answer to this question.

So let's compare:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

We isolated the root, got non-negative numbers on both sides of the inequality, so we have the right to square both sides:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

I think it's a no brainer that $4\sqrt(13) \gt 3$, so $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) (2)$, finally the points on the axes will be arranged like this:
Case of ugly roots
Let me remind you that we are solving a set, so the answer will be the union, and not the intersection of the shaded sets.

Answer: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

As you can see, our scheme works great both for simple tasks and for very hard ones. The only “weak spot” in this approach is that you need to correctly compare irrational numbers (and believe me: these are not only roots). But a separate (and very serious lesson) will be devoted to questions of comparison. And we move on.

3. Inequalities with non-negative "tails"

So we got to the most interesting. These are inequalities of the form:

\[\left| f\right| \gt\left| g\right|\]

Generally speaking, the algorithm that we are going to talk about now is true only for the module. It works in all inequalities where there are guaranteed non-negative expressions on the left and right:

What to do with these tasks? Just remember:

In inequalities with non-negative tails, both sides can be raised to any natural power. There will be no additional restrictions.

First of all, we will be interested in squaring - it burns modules and roots:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\end(align)\]

Just do not confuse this with taking the root of the square:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Countless mistakes were made when a student forgot to install a module! But this is a completely different story (these are, as it were, irrational equations), so we will not go into it now. Let's better solve a couple of problems:

A task. Solve the inequality:

\[\left| x+2 \right|\ge \left| 1-2x \right|\]

Decision. We immediately notice two things:

This is a non-strict inequality. Points on the number line will be punched out.

Both sides of the inequality are obviously non-negative (this is a property of the module: $\left| f\left(x \right) \right|\ge 0$).

Therefore, we can square both sides of the inequality to get rid of the modulus and solve the problem using the usual interval method:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\end(align)\]

At the last step, I cheated a little: I changed the sequence of terms, using the parity of the modulus (in fact, I multiplied the expression $1-2x$ by −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ right)\right)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

We solve by the interval method. Let's move from inequality to equation:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(align)\]

We mark the found roots on the number line. Once again: all points are shaded because the original inequality is not strict!
Getting rid of the module sign
Let me remind you for the especially stubborn: we take the signs from the last inequality, which was written down before moving on to the equation. And we paint over the areas required in the same inequality. In our case, this is $\left(x-3 \right)\left(3x+1 \right)\le 0$.

That's it. Problem solved.

Answer: $x\in \left[ -\frac(1)(3);3 \right]$.

A task. Solve the inequality:

\[\left| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]

Decision. We do everything the same. I will not comment - just look at the sequence of actions.

Let's square it:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ right))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Spacing method:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Rightarrow x=-1.5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varnothing . \\\end(align)\]

There is only one root on the number line:
The answer is a whole range
Answer: $x\in \left[ -1.5;+\infty \right)$.

A small note about the last task. As one of my students accurately noted, both submodule expressions in this inequality are obviously positive, so the modulus sign can be omitted without harm to health.

But this is already a completely different level of thinking and a different approach - it can be conditionally called the method of consequences. About him - in a separate lesson. And now let's move on to the final part of today's lesson and consider a universal algorithm that always works. Even when all previous approaches were powerless. :)

4. Method of enumeration of options

What if all these tricks don't work? If the inequality does not reduce to non-negative tails, if it is impossible to isolate the module, if at all pain-sadness-longing?

Then the “heavy artillery” of all mathematics enters the scene - the enumeration method. With regard to inequalities with the modulus, it looks like this:

Write out all submodule expressions and equate them to zero;
Solve the resulting equations and mark the found roots on one number line;
The straight line will be divided into several sections, within which each module has a fixed sign and therefore unambiguously expands;
Solve the inequality on each such section (you can separately consider the boundary roots obtained in paragraph 2 - for reliability). Combine the results - this will be the answer. :)

Well, how? Weak? Easy! Only for a long time. Let's see in practice:

A task. Solve the inequality:

\[\left| x+2 \right| \lt\left| x-1 \right|+x-\frac(3)(2)\]

Decision. This crap doesn't boil down to inequalities like $\left| f\right| \lt g$, $\left| f\right| \gt g$ or $\left| f\right| \lt\left| g \right|$, so let's go ahead.

We write out submodule expressions, equate them to zero and find the roots:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Rightarrow x=1. \\\end(align)\]

In total, we have two roots that divide the number line into three sections, inside which each module is revealed uniquely:
Splitting the number line by zeros of submodular functions
Let's consider each section separately.

1. Let $x \lt -2$. Then both submodule expressions are negative, and the original inequality is rewritten as follows:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end(align)\]

We got a fairly simple constraint. Let's intersect it with the original assumption that $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Obviously, the variable $x$ cannot simultaneously be less than −2 but greater than 1.5. There are no solutions in this area.

1.1. Let's separately consider the boundary case: $x=-2$. Let's just substitute this number into the original inequality and check: does it hold?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \right|-2-1.5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0,5\Rightarrow \varnothing . \\\end(align)\]

Obviously, the chain of calculations has led us to the wrong inequality. Therefore, the original inequality is also false, and $x=-2$ is not included in the answer.

2. Now let $-2 \lt x \lt 1$. The left module will already open with a "plus", but the right one is still with a "minus". We have:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt -2.5 \\\end(align)\]

Again we intersect with the original requirement:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

And again, the empty set of solutions, since there are no numbers that are both less than −2.5 and greater than −2.

2.1. And again a special case: $x=1$. We substitute into the original inequality:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \left| 3\right| \lt\left| 0 \right|+1-1.5; \\ & 3 \lt -0.5; \\ & 3 \lt -0,5\Rightarrow \varnothing . \\\end(align)\]

Similarly to the previous "special case", the number $x=1$ is clearly not included in the answer.

3. The last piece of the line: $x \gt 1$. Here all modules are expanded with a plus sign:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\]

And again we intersect the found set with the original constraint:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \right)\]

Finally! We have found the interval, which will be the answer.

Answer: $x\in \left(4,5;+\infty \right)$

Finally, one note that may save you from stupid mistakes when solving real problems:

Solutions of inequalities with modules are usually continuous sets on the number line - intervals and segments. Isolated points are much rarer. And even more rarely, it happens that the boundaries of the solution (the end of the segment) coincide with the boundary of the range under consideration.

Therefore, if the boundaries (those very “special cases”) are not included in the answer, then the areas to the left-right of these boundaries will almost certainly not be included in the answer either. And vice versa: the border entered in response, which means that some areas around it will also be responses.

Keep this in mind when you check your solutions.

And today not everyone can solve rational inequalities. More precisely, not only everyone can decide. Few people can do it.
Klitschko

This lesson is going to be tough. So tough that only the Chosen will reach the end of it. Therefore, before reading, I recommend removing women, cats, pregnant children and ...

Okay, it's actually quite simple. Suppose you have mastered the interval method (if you have not mastered it, I recommend you go back and read it) and learned how to solve inequalities of the form $P\left(x \right) \gt 0$, where $P\left(x \right)$ is some polynomial or product of polynomials.

I believe that it will not be difficult for you to solve, for example, such a game (by the way, try it for a warm-up):

\[\begin(align) & \left(2((x)^(2))+3x+4 \right)\left(4x+25 \right) \gt 0; \\ & x\left(2((x)^(2))-3x-20 \right)\left(x-1 \right)\ge 0; \\ & \left(8x-((x)^(4)) \right)((\left(x-5 \right))^(6))\le 0. \\ \end(align)\]

Now let's complicate the task a little and consider not just polynomials, but the so-called rational fractions of the form:

where $P\left(x \right)$ and $Q\left(x \right)$ are the same polynomials of the form $((a)_(n))((x)^(n))+(( a)_(n-1))((x)^(n-1))+...+((a)_(0))$, or the product of such polynomials.

This will be a rational inequality. The fundamental point is the presence of the variable $x$ in the denominator. For example, here are rational inequalities:

\[\begin(align) & \frac(x-3)(x+7) \lt 0; \\ & \frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0; \\ & \frac(3((x)^(2))+10x+3)(((\left(3-x \right))^(2))\left(4-((x)^( 2)) \right))\ge 0. \\ \end(align)\]

And this is not a rational, but the most common inequality, which is solved by the interval method:

\[\frac(((x)^(2))+6x+9)(5)\ge 0\]

Looking ahead, I’ll say right away: there are at least two ways to solve rational inequalities, but all of them in one way or another are reduced to the method of intervals already known to us. Therefore, before analyzing these methods, let's recall the old facts, otherwise there will be no sense from the new material.

What you already need to know

There are not many important facts. We really only need four.

Abbreviated multiplication formulas

Yes, yes: they will haunt us throughout the school math curriculum. And at the university too. There are quite a few of these formulas, but we only need the following:

\[\begin(align) & ((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \right))^(2)); \\ & ((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right); \\ & ((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b) ^(2))\right); \\ & ((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+((b)^( 2))\right). \\ \end(align)\]

Pay attention to the last two formulas - this is the sum and difference of cubes (and not the cube of the sum or difference!). They are easy to remember if you notice that the sign in the first bracket is the same as the sign in the original expression, and in the second bracket it is opposite to the sign in the original expression.

Linear equations

These are the simplest equations of the form $ax+b=0$, where $a$ and $b$ are ordinary numbers, and $a\ne 0$. This equation is easy to solve:

\[\begin(align) & ax+b=0; \\ &ax=-b; \\ & x=-\frac(b)(a). \\ \end(align)\]

I note that we have the right to divide by the coefficient $a$, because $a\ne 0$. This requirement is quite logical, since with $a=0$ we get this:

First, there is no $x$ variable in this equation. This, generally speaking, should not confuse us (this happens, say, in geometry, and quite often), but still we are no longer a linear equation.

Secondly, the solution of this equation depends solely on the coefficient $b$. If $b$ is also zero, then our equation is $0=0$. This equality is always true; hence $x$ is any number (usually written as $x\in \mathbb(R)$). If the coefficient $b$ is not equal to zero, then the equality $b=0$ is never satisfied, i.e. no answers (written $x\in \varnothing $ and read "solution set is empty").

To avoid all these complexities, we simply assume $a\ne 0$, which does not in any way restrict us from further reflections.

Quadratic equations

Let me remind you that this is called a quadratic equation:

Here on the left is a polynomial of the second degree, and again $a\ne 0$ (otherwise, instead of a quadratic equation, we get a linear one). The following equations are solved through the discriminant:

If $D \gt 0$, we get two different roots;
If $D=0$, then the root will be one, but of the second multiplicity (what kind of multiplicity it is and how to take it into account - more on that later). Or we can say that the equation has two identical roots;
For $D \lt 0$ there are no roots at all, and the sign of the polynomial $a((x)^(2))+bx+c$ for any $x$ coincides with the sign of the coefficient $a$. This, by the way, is a very useful fact, which for some reason is forgotten to be told in algebra classes.

The roots themselves are calculated according to the well-known formula:

\[((x)_(1,2))=\frac(-b\pm \sqrt(D))(2a)\]

Hence, by the way, the restrictions on the discriminant. After all, the square root of a negative number does not exist. As for the roots, many students have a terrible mess in their heads, so I specially recorded a whole lesson: what is a root in algebra and how to calculate it - I highly recommend reading it. :)

Operations with rational fractions

Everything that was written above, you already know if you studied the method of intervals. But what we will analyze now has no analogues in the past - this is a completely new fact.

Definition. A rational fraction is an expression of the form

\[\frac(P\left(x \right))(Q\left(x \right))\]

where $P\left(x \right)$ and $Q\left(x \right)$ are polynomials.

It is obvious that it is easy to obtain an inequality from such a fraction - it is enough just to attribute the sign “greater than” or “less than” to the right. And a little further we will find that solving such problems is a pleasure, everything is very simple there.

Problems begin when there are several such fractions in one expression. They have to be reduced to a common denominator - and it is at this moment that a large number of offensive mistakes are made.

Therefore, in order to successfully solve rational equations, it is necessary to firmly master two skills:

Factorization of the polynomial $P\left(x \right)$;
Actually, bringing fractions to a common denominator.

How to factorize a polynomial? Very simple. Let we have a polynomial of the form

Let's equate it to zero. We get the $n$-th degree equation:

\[((a)_(n))((x)^(n))+((a)_(n-1))((x)^(n-1))+...+(( a)_(1))x+((a)_(0))=0\]

Let's say we solved this equation and got the roots $((x)_(1)),\ ...,\ ((x)_(n))$ (don't worry: in most cases there will be no more than two of these roots) . In this case, our original polynomial can be rewritten like this:

\[\begin(align) & P\left(x \right)=((a)_(n))((x)^(n))+((a)_(n-1))((x )^(n-1))+...+((a)_(1))x+((a)_(0))= \\ & =((a)_(n))\left(x -((x)_(1)) \right)\cdot \left(x-((x)_(2)) \right)\cdot ...\cdot \left(x-((x)_( n)) \right) \end(align)\]

That's all! Please note: the leading coefficient $((a)_(n))$ has not disappeared anywhere - it will be a separate factor in front of the brackets, and if necessary, it can be inserted into any of these brackets (practice shows that with $((a)_ (n))\ne \pm 1$ there are almost always fractions among the roots).

A task. Simplify the expression:

\[\frac(((x)^(2))+x-20)(x-4)-\frac(2((x)^(2))-5x+3)(2x-3)-\ frac(4-8x-5((x)^(2)))(x+2)\]

Decision. First, let's look at the denominators: they are all linear binomials, and there is nothing to factorize here. So let's factorize the numerators:

\[\begin(align) & ((x)^(2))+x-20=\left(x+5 \right)\left(x-4 \right); \\ & 2((x)^(2))-5x+3=2\left(x-\frac(3)(2) \right)\left(x-1 \right)=\left(2x- 3\right)\left(x-1\right); \\ & 4-8x-5((x)^(2))=-5\left(x+2 \right)\left(x-\frac(2)(5) \right)=\left(x +2 \right)\left(2-5x \right). \\\end(align)\]

Please note: in the second polynomial, the senior coefficient "2", in full accordance with our scheme, first appeared in front of the bracket, and then was included in the first bracket, since a fraction got out there.

The same thing happened in the third polynomial, only there the order of the terms is also confused. However, the coefficient “−5” ended up being included in the second bracket (remember: you can enter a factor in one and only one bracket!), which saved us from the inconvenience associated with fractional roots.

As for the first polynomial, everything is simple there: its roots are sought either in the standard way through the discriminant, or using the Vieta theorem.

Let's go back to the original expression and rewrite it with the numerators decomposed into factors:

\[\begin(matrix) \frac(\left(x+5 \right)\left(x-4 \right))(x-4)-\frac(\left(2x-3 \right)\left( x-1 \right))(2x-3)-\frac(\left(x+2 \right)\left(2-5x \right))(x+2)= \\ =\left(x+5 \right)-\left(x-1 \right)-\left(2-5x \right)= \\ =x+5-x+1-2+5x= \\ =5x+4. \\ \end(matrix)\]

Answer: $5x+4$.

As you can see, nothing complicated. A bit of 7th-8th grade math and that's it. The point of all transformations is to turn a complex and scary expression into something simple and easy to work with.

However, this will not always be the case. So now we will consider a more serious problem.

But first, let's figure out how to bring two fractions to a common denominator. The algorithm is extremely simple:

Factorize both denominators;
Consider the first denominator and add to it the factors present in the second denominator, but not in the first. The resulting product will be the common denominator;
Find out what factors each of the original fractions lacks so that the denominators become equal to the common one.

Perhaps this algorithm will seem to you just a text in which there are “a lot of letters”. So let's take a look at a specific example.

A task. Simplify the expression:

\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \right)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \right)\]

Decision. Such voluminous tasks are best solved in parts. Let's write out what is in the first bracket:

\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3))-8 )-\frac(1)(x-2)\]

Unlike the previous problem, here the denominators are not so simple. Let's factorize each of them.

The square trinomial $((x)^(2))+2x+4$ cannot be factorized because the equation $((x)^(2))+2x+4=0$ has no roots (the discriminant is negative). We leave it unchanged.

The second denominator, the cubic polynomial $((x)^(3))-8$, upon closer examination is the difference of cubes and can be easily decomposed using the abbreviated multiplication formulas:

\[((x)^(3))-8=((x)^(3))-((2)^(3))=\left(x-2 \right)\left(((x) ^(2))+2x+4 \right)\]

Nothing else can be factored, since the first bracket contains a linear binomial, and the second one contains a construction already familiar to us, which has no real roots.

Finally, the third denominator is a linear binomial that cannot be decomposed. Thus, our equation will take the form:

\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\left(x-2 \right)\left (((x)^(2))+2x+4 \right))-\frac(1)(x-2)\]

It is quite obvious that $\left(x-2 \right)\left(((x)^(2))+2x+4 \right)$ will be the common denominator, and to reduce all fractions to it, you need to multiply the first fraction to $\left(x-2 \right)$, and the last one to $\left(((x)^(2))+2x+4 \right)$. Then it remains only to bring the following:

\[\begin(matrix) \frac(x\cdot \left(x-2 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \ right))+\frac(((x)^(2))+8)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))- \frac(1\cdot \left(((x)^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x +4 \right))= \\ =\frac(x\cdot \left(x-2 \right)+\left(((x)^(2))+8 \right)-\left(((x )^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))= \\ =\frac (((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \right)\left (((x)^(2))+2x+4 \right))= \\ =\frac(((x)^(2))-4x+4)(\left(x-2 \right)\ left(((x)^(2))+2x+4 \right)). \\ \end(matrix)\]

Pay attention to the second line: when the denominator is already common, i.e. instead of three separate fractions, we wrote one large one, you should not immediately get rid of the brackets. It is better to write an extra line and note that, say, there was a minus before the third fraction - and it will not go anywhere, but will “hang” in the numerator in front of the bracket. This will save you a lot of mistakes.

Well, in the last line it is useful to factorize the numerator. Moreover, this is an exact square, and the abbreviated multiplication formulas again come to our aid. We have:

\[\frac(((x)^(2))-4x+4)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))= \frac(((\left(x-2 \right))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right) )=\frac(x-2)(((x)^(2))+2x+4)\]

Now let's deal with the second bracket in the same way. Here I will simply write a chain of equalities:

\[\begin(matrix) \frac(((x)^(2)))(((x)^(2))-4)-\frac(2)(2-x)=\frac((( x)^(2)))(\left(x-2 \right)\left(x+2 \right))-\frac(2)(2-x)= \\ =\frac(((x) ^(2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2)(x-2)= \\ =\frac(((x)^( 2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2\cdot \left(x+2 \right))(\left(x-2 \right )\cdot \left(x+2 \right))= \\ =\frac(((x)^(2))+2\cdot \left(x+2 \right))(\left(x-2 \right)\left(x+2 \right))=\frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right) ). \\ \end(matrix)\]

We return to the original problem and look at the product:

\[\frac(x-2)(((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right))=\frac(1)(x+2)\]

Answer: \[\frac(1)(x+2)\].

The meaning of this problem is the same as the previous one: to show how much rational expressions can be simplified if you approach their transformation wisely.

And now, when you know all this, let's move on to the main topic of today's lesson - solving fractional rational inequalities. Moreover, after such preparation, the inequalities themselves will click like nuts. :)

The main way to solve rational inequalities

There are at least two approaches to solving rational inequalities. Now we will consider one of them - the one that is generally accepted in the school mathematics course.

But first, let's note an important detail. All inequalities are divided into two types:

Strict: $f\left(x \right) \gt 0$ or $f\left(x \right) \lt 0$;
Nonstrict: $f\left(x \right)\ge 0$ or $f\left(x \right)\le 0$.

Inequalities of the second type are easily reduced to the first, as well as the equation:

This small "addition" $f\left(x \right)=0$ leads to such an unpleasant thing as filled points - we met them back in the interval method. Otherwise, there are no differences between strict and non-strict inequalities, so let's analyze the universal algorithm:

Collect all non-zero elements on one side of the inequality sign. For example, on the left;

Bring all fractions to a common denominator (if there are several such fractions), bring similar ones. Then, if possible, factorize into the numerator and denominator. One way or another, we get an inequality of the form $\frac(P\left(x \right))(Q\left(x \right))\vee 0$, where the tick is the inequality sign.

Equate the numerator to zero: $P\left(x \right)=0$. We solve this equation and get the roots $((x)_(1))$, $((x)_(2))$, $((x)_(3))$, ... Then we require that the denominator was not equal to zero: $Q\left(x \right)\ne 0$. Of course, in essence, we have to solve the equation $Q\left(x \right)=0$, and we get the roots $x_(1)^(*)$, $x_(2)^(*)$, $x_(3 )^(*)$, ... (in real problems there will hardly be more than three such roots).

We mark all these roots (both with and without asterisks) on a single number line, and the roots without stars are painted over, and those with stars are punched out.

We place the plus and minus signs, select the intervals that we need. If the inequality has the form $f\left(x \right) \gt 0$, then the answer will be the intervals marked with a "plus". If $f\left(x \right) \lt 0$, then we look at intervals with "minuses".

Practice shows that points 2 and 4 cause the greatest difficulties - competent transformations and the correct arrangement of numbers in ascending order. Well, at the last step, be extremely careful: we always place signs based on the last inequality written before moving on to the equations. This is a universal rule inherited from the interval method.

So, there is a scheme. Let's practice.

A task. Solve the inequality:

\[\frac(x-3)(x+7) \lt 0\]

Decision. We have a strict inequality of the form $f\left(x \right) \lt 0$. Obviously, points 1 and 2 from our scheme have already been completed: all the elements of inequality are collected on the left, nothing needs to be reduced to a common denominator. So let's move on to the third point.

Set the numerator to zero:

\[\begin(align) & x-3=0; \\ &x=3. \end(align)\]

And the denominator:

\[\begin(align) & x+7=0; \\ & ((x)^(*))=-7. \\ \end(align)\]

In this place, many people get stuck, because in theory you need to write down $x+7\ne 0$, as required by the ODZ (you can’t divide by zero, that’s all). But after all, in the future we will poke out the points that came from the denominator, so you shouldn’t complicate your calculations once again - write an equal sign everywhere and don’t worry. No one will deduct points for this. :)

Fourth point. We mark the obtained roots on the number line:
All points are punctured because the inequality is strict
Note: all points are punctured because the original inequality is strict. And here it doesn’t matter anymore: these points came from the numerator or from the denominator.

Well, look at the signs. Take any number $((x)_(0)) \gt 3$. For example, $((x)_(0))=100$ (but you could have just as well taken $((x)_(0))=3.1$ or $((x)_(0)) =1\000\000$). We get:

So, to the right of all the roots we have a positive area. And when passing through each root, the sign changes (this will not always be the case, but more on that later). Therefore, we proceed to the fifth point: we place the signs and choose the right one:

We return to the last inequality, which was before solving the equations. Actually, it coincides with the original one, because we did not perform any transformations in this task.

Since it is necessary to solve an inequality of the form $f\left(x \right) \lt 0$, I shaded the interval $x\in \left(-7;3 \right)$ - it is the only one marked with a minus sign. This is the answer.

Answer: $x\in \left(-7;3 \right)$

That's all! Is it difficult? No, it's not difficult. Indeed, it was an easy task. Now let's complicate the mission a little and consider a more "fancy" inequality. When solving it, I will no longer give such detailed calculations - I will simply outline the key points. In general, we will arrange it the way we would have done it on an independent work or exam. :)

A task. Solve the inequality:

\[\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0\]

Decision. This is a non-strict inequality of the form $f\left(x \right)\ge 0$. All non-zero elements are collected on the left, there are no different denominators. Let's move on to equations.

Numerator:

\[\begin(align) & \left(7x+1 \right)\left(11x+2 \right)=0 \\ & 7x+1=0\Rightarrow ((x)_(1))=-\ frac(1)(7); \\ & 11x+2=0\Rightarrow ((x)_(2))=-\frac(2)(11). \\ \end(align)\]

Denominator:

\[\begin(align) & 13x-4=0; \\ & 13x=4; \\ & ((x)^(*))=\frac(4)(13). \\ \end(align)\]

I don’t know what kind of pervert made up this problem, but the roots didn’t turn out very well: it will be difficult to arrange them on a number line. And if everything is more or less clear with the root $((x)^(*))=(4)/(13)\;$ (this is the only positive number - it will be on the right), then $((x)_(1 ))=-(1)/(7)\;$ and $((x)_(2))=-(2)/(11)\;$ require further study: which one is larger?

You can find this out, for example:

\[((x)_(1))=-\frac(1)(7)=-\frac(2)(14) \gt -\frac(2)(11)=((x)_(2 ))\]

I hope there is no need to explain why the numeric fraction $-(2)/(14)\; \gt -(2)/(11)\;$? If necessary, I recommend remembering how to perform actions with fractions.

And we mark all three roots on the number line:
The points from the numerator are shaded, from the denominator they are cut out
We put up signs. For example, you can take $((x)_(0))=1$ and find out the sign at this point:

\[\begin(align) & f\left(x \right)=\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4); \\ & f\left(1 \right)=\frac(\left(7\cdot 1+1 \right)\left(11\cdot 1+2 \right))(13\cdot 1-4)=\ frac(8\cdot 13)(9) \gt 0. \\\end(align)\]

The last inequality before the equations was $f\left(x \right)\ge 0$, so we are interested in the plus sign.

We got two sets: one is an ordinary segment, and the other is an open ray on the number line.

Answer: $x\in \left[ -\frac(2)(11);-\frac(1)(7) \right]\bigcup \left(\frac(4)(13);+\infty \right )$

An important note about the numbers that we substitute to find out the sign on the rightmost interval. It is not necessary to substitute a number close to the rightmost root. You can take billions or even "plus-infinity" - in this case, the sign of the polynomial in the bracket, numerator or denominator is determined solely by the sign of the leading coefficient.

Let's take another look at the $f\left(x \right)$ function from the last inequality:

It contains three polynomials:

\[\begin(align) & ((P)_(1))\left(x \right)=7x+1; \\ & ((P)_(2))\left(x \right)=11x+2; \\ & Q\left(x\right)=13x-4. \end(align)\]

All of them are linear binomials, and all of them have positive coefficients (numbers 7, 11 and 13). Therefore, when substituting very large numbers, the polynomials themselves will also be positive. :)

This rule may seem overly complicated, but only at first, when we analyze very easy problems. In serious inequalities, the "plus-infinity" substitution will allow us to figure out the signs much faster than the standard $((x)_(0))=100$.

We will face such challenges very soon. But first, let's look at an alternative way to solve fractional rational inequalities.

Alternative way

This technique was suggested to me by one of my students. I myself have never used it, but practice has shown that it is really more convenient for many students to solve inequalities in this way.

So, the original data is the same. We need to solve a fractional rational inequality:

\[\frac(P\left(x \right))(Q\left(x \right)) \gt 0\]

Let's think: why is the polynomial $Q\left(x \right)$ "worse" than the polynomial $P\left(x \right)$? Why do we have to consider separate groups of roots (with and without an asterisk), think about punched points, etc.? It's simple: a fraction has a domain of definition, according to which the fraction makes sense only when its denominator is different from zero.

Otherwise, there are no differences between the numerator and the denominator: we also equate it to zero, look for the roots, then mark them on the number line. So why not replace the fractional bar (in fact, the division sign) with the usual multiplication, and write all the requirements of the DHS as a separate inequality? For example, like this:

\[\frac(P\left(x \right))(Q\left(x \right)) \gt 0\Rightarrow \left\( \begin(align) & P\left(x \right)\cdot Q \left(x \right) \gt 0, \\ & Q\left(x \right)\ne 0. \\ \end(align) \right.\]

Please note: this approach will allow you to reduce the problem to the method of intervals, but it will not complicate the solution at all. After all, anyway, we will equate the polynomial $Q\left(x \right)$ to zero.

Let's see how it works on real tasks.

A task. Solve the inequality:

\[\frac(x+8)(x-11) \gt 0\]

Decision. So, let's move on to the interval method:

\[\frac(x+8)(x-11) \gt 0\Rightarrow \left\( \begin(align) & \left(x+8 \right)\left(x-11 \right) \gt 0 , \\ & x-11\ne 0. \\ \end(align) \right.\]

The first inequality is solved elementarily. Just set each parenthesis to zero:

\[\begin(align) & x+8=0\Rightarrow ((x)_(1))=-8; \\ & x-11=0\Rightarrow ((x)_(2))=11. \\ \end(align)\]

With the second inequality, everything is also simple:

We mark the points $((x)_(1))$ and $((x)_(2))$ on the real line. All of them are punctured because the inequality is strict:
The right point turned out to be punctured twice. This is fine.
Pay attention to the point $x=11$. It turns out that it is “twice gouged out”: on the one hand, we gouge it out because of the severity of inequality, on the other hand, because of the additional requirement of ODZ.

In any case, it will be just a punctured point. Therefore, we put signs for the inequality $\left(x+8 \right)\left(x-11 \right) \gt 0$ - the last one we saw before we started solving the equations:

We are interested in positive regions, since we are solving an inequality of the form $f\left(x \right) \gt 0$, and we will color them. It remains only to write down the answer.

Answer. $x\in \left(-\infty ;-8 \right)\bigcup \left(11;+\infty \right)$

Using this solution as an example, I would like to warn you against a common mistake among novice students. Namely: never open parentheses in inequalities! On the contrary, try to factor everything - this will simplify the solution and save you a lot of problems.

Now let's try something more difficult.

A task. Solve the inequality:

\[\frac(\left(2x-13 \right)\left(12x-9 \right))(15x+33)\le 0\]

Decision. This is a non-strict inequality of the form $f\left(x \right)\le 0$, so here you need to carefully monitor the filled points.

Let's move on to the interval method:

\[\left\( \begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)\le 0, \\ & 15x+33\ ne 0. \\ \end(align) \right.\]

Let's move on to the equation:

\[\begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)=0 \\ & 2x-13=0\Rightarrow ((x )_(1))=6.5; \\ & 12x-9=0\Rightarrow ((x)_(2))=0.75; \\ & 15x+33=0\Rightarrow ((x)_(3))=-2,2. \\ \end(align)\]

We take into account the additional requirement:

We mark all the obtained roots on the number line:
If a point is both punched out and filled in at the same time, it is considered punched out.
Again, two points "overlap" each other - this is normal, it will always be so. It is only important to understand that a point marked both as punched out and filled in is actually a punched out point. Those. "Gouging" is a stronger action than "painting over".

This is absolutely logical, because by puncturing we mark points that affect the sign of the function, but do not themselves participate in the answer. And if at some point the number ceases to suit us (for example, it does not fall into the ODZ), we delete it from consideration until the very end of the task.

In general, stop philosophizing. We arrange the signs and paint over those intervals that are marked with a minus sign:

Answer. $x\in \left(-\infty ;-2,2 \right)\bigcup \left[ 0,75;6,5 \right]$.

And again I wanted to draw your attention to this equation:

\[\left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)=0\]

Once again: never open parentheses in such equations! You're only making it harder for yourself. Remember: the product is zero when at least one of the factors is zero. Consequently, this equation simply “falls apart” into several smaller ones, which we solved in the previous problem.

Taking into account the multiplicity of roots

From the previous problems, it is easy to see that it is precisely the non-strict inequalities that are most difficult, because in them you have to keep track of the filled points.

But there is an even greater evil in the world - these are multiple roots in inequalities. Here it is already necessary to follow not some filled points there - here the inequality sign may not suddenly change when passing through these same points.

We have not yet considered anything like this in this lesson (although a similar problem was often encountered in the interval method). So let's introduce a new definition:

Definition. The root of the equation $((\left(x-a \right))^(n))=0$ is equal to $x=a$ and is called the root of the $n$th multiplicity.

Actually, we are not particularly interested in the exact value of the multiplicity. The only important thing is whether this very number $n$ is even or odd. Because:

If $x=a$ is a root of even multiplicity, then the sign of the function does not change when passing through it;
And vice versa, if $x=a$ is a root of odd multiplicity, then the sign of the function will change.

A special case of a root of odd multiplicity are all the previous problems considered in this lesson: there the multiplicity is equal to one everywhere.

And further. Before we start solving problems, I would like to draw your attention to one subtlety that seems obvious to an experienced student, but drives many beginners into a stupor. Namely:

The multiplicity root $n$ occurs only when the entire expression is raised to this power: $((\left(x-a \right))^(n))$, and not $\left(((x)^( n))-a\right)$.

Once again: the bracket $((\left(x-a \right))^(n))$ gives us the root $x=a$ of multiplicity $n$, but the bracket $\left(((x)^(n)) -a \right)$ or, as often happens, $(a-((x)^(n)))$ gives us a root (or two roots, if $n$ is even) of the first multiplicity, no matter what is equal to $n$.

Compare:

\[((\left(x-3 \right))^(5))=0\Rightarrow x=3\left(5k \right)\]

Everything is clear here: the whole bracket was raised to the fifth power, so at the output we got the root of the fifth degree. And now:

\[\left(((x)^(2))-4 \right)=0\Rightarrow ((x)^(2))=4\Rightarrow x=\pm 2\]

We got two roots, but both of them have the first multiplicity. Or here's another one:

\[\left(((x)^(10))-1024 \right)=0\Rightarrow ((x)^(10))=1024\Rightarrow x=\pm 2\]

And do not be confused by the tenth degree. The main thing is that 10 is an even number, so we have two roots at the output, and both of them again have the first multiplicity.

In general, be careful: multiplicity occurs only when the degree applies to the entire bracket, not just the variable.

A task. Solve the inequality:

\[\frac(((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right))(((\left(x+7 \right))^(5)))\ge 0\]

Decision. Let's try to solve it in an alternative way - through the transition from the particular to the product:

\[\left\( \begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ( (\left(x+7 \right))^(5))\ge 0, \\ & ((\left(x+7 \right))^(5))\ne 0. \\ \end(align )\right.\]

We deal with the first inequality using the interval method:

\[\begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ((\left( x+7 \right))^(5))=0; \\ & ((x)^(2))=0\Rightarrow x=0\left(2k \right); \\ & ((\left(6-x \right))^(3))=0\Rightarrow x=6\left(3k \right); \\ & x+4=0\Rightarrow x=-4; \\ & ((\left(x+7 \right))^(5))=0\Rightarrow x=-7\left(5k \right). \\ \end(align)\]

Additionally, we solve the second inequality. In fact, we have already solved it, but so that the reviewers do not find fault with the solution, it is better to solve it again:

\[((\left(x+7 \right))^(5))\ne 0\Rightarrow x\ne -7\]

Note that there are no multiplicities in the last inequality. Indeed: what difference does it make how many times to cross out the point $x=-7$ on the number line? At least once, at least five times - the result will be the same: a punctured point.

Let's note everything that we got on the number line:

As I said, the $x=-7$ point will eventually be punched out. The multiplicities are arranged based on the solution of the inequality by the interval method.

It remains to place the signs:

Since the point $x=0$ is a root of even multiplicity, the sign does not change when passing through it. The remaining points have an odd multiplicity, and everything is simple with them.

Answer. $x\in \left(-\infty ;-7 \right)\bigcup \left[ -4;6 \right]$

Pay attention to $x=0$ again. Because of the even multiplicity, an interesting effect arises: everything to the left of it is painted over, to the right - too, and the point itself is completely painted over.

As a consequence, it does not need to be isolated when recording a response. Those. you don't have to write something like $x\in \left[ -4;0 \right]\bigcup \left[ 0;6 \right]$ (although formally such an answer would also be correct). Instead, we immediately write $x\in \left[ -4;6 \right]$.

Such effects are possible only for roots of even multiplicity. And in the next task, we will encounter the reverse "manifestation" of this effect. Ready?

A task. Solve the inequality:

\[\frac(((\left(x-3 \right))^(4))\left(x-4 \right))(((\left(x-1 \right))^(2)) \left(7x-10-((x)^(2)) \right))\ge 0\]

Decision. This time we will follow the standard scheme. Set the numerator to zero:

\[\begin(align) & ((\left(x-3 \right))^(4))\left(x-4 \right)=0; \\ & ((\left(x-3 \right))^(4))=0\Rightarrow ((x)_(1))=3\left(4k \right); \\ & x-4=0\Rightarrow ((x)_(2))=4. \\ \end(align)\]

And the denominator:

\[\begin(align) & ((\left(x-1 \right))^(2))\left(7x-10-((x)^(2)) \right)=0; \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(1)^(*)=1\left(2k \right); \\ & 7x-10-((x)^(2))=0\Rightarrow x_(2)^(*)=5;\ x_(3)^(*)=2. \\ \end(align)\]

Since we are solving a non-strict inequality of the form $f\left(x \right)\ge 0$, the roots from the denominator (which have asterisks) will be cut out, and those from the numerator will be painted over.

We arrange the signs and stroke the areas marked with a "plus":
The point $x=3$ is isolated. This is part of the answer
Before writing down the final answer, take a close look at the picture:

The point $x=1$ has an even multiplicity, but is itself punctured. Therefore, it will have to be isolated in the answer: you need to write $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)$, and not $x\in \left(-\ infty ;2\right)$.

The point $x=3$ also has an even multiplicity and is shaded. The arrangement of signs indicates that the point itself suits us, but a step to the left and right - and we find ourselves in an area that definitely does not suit us. Such points are called isolated and are written as $x\in \left$ 3 \right$$.

We combine all the obtained pieces into a common set and write down the answer.

Answer: $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)\bigcup \left$ 3 \right$\bigcup \left[ 4;5 \right) $

Definition. Solving the inequality means find the set of all its solutions, or prove that this set is empty.

It would seem: what can be incomprehensible here? Yes, the fact of the matter is that sets can be specified in different ways. Let's rewrite the answer to the last problem:

We literally read what is written. The variable "x" belongs to a certain set, which is obtained by the union (symbol "U") of four separate sets:

The interval $\left(-\infty ;1 \right)$, which literally means "all numbers less than one, but not one itself";
The interval is $\left(1;2 \right)$, i.e. "all numbers between 1 and 2, but not the numbers 1 and 2 themselves";
The set $\left$ 3 \right$$, consisting of a single number - three;
The interval $\left[ 4;5 \right)$ containing all numbers between 4 and 5, plus 4 itself, but not 5.

The third point is of interest here. Unlike intervals, which define infinite sets of numbers and only denote only the boundaries of these sets, the set $\left$ 3 \right$$ defines exactly one number by enumeration.

To understand that we are listing the specific numbers included in the set (and not setting boundaries or anything else), curly braces are used. For example, the notation $\left$ 1;2 \right$$ means exactly "a set consisting of two numbers: 1 and 2", but not a segment from 1 to 2. In no case do not confuse these concepts.

Multiplicity addition rule

Well, at the end of today's lesson, a little tin from Pavel Berdov. :)

Attentive students have probably already asked themselves the question: what will happen if the same roots are found in the numerator and denominator? So the following rule works:

Multiplicities of identical roots are added. Is always. Even if this root occurs in both the numerator and the denominator.

Sometimes it's better to decide than to talk. Therefore, we solve the following problem:

A task. Solve the inequality:

\[\frac(((x)^(2))+6x+8)(\left(((x)^(2))-16 \right)\left(((x)^(2))+ 9x+14 \right))\ge 0\]

\[\begin(align) & ((x)^(2))+6x+8=0 \\ & ((x)_(1))=-2;\ ((x)_(2))= -4. \\ \end(align)\]

So far, nothing special. Set the denominator to zero:

\[\begin(align) & \left(((x)^(2))-16 \right)\left(((x)^(2))+9x+14 \right)=0 \\ & ( (x)^(2))-16=0\Rightarrow x_(1)^(*)=4;\ x_(2)^(*)=-4; \\ & ((x)^(2))+9x+14=0\Rightarrow x_(3)^(*)=-7;\ x_(4)^(*)=-2. \\ \end(align)\]

Two identical roots are found: $((x)_(1))=-2$ and $x_(4)^(*)=-2$. Both have the first multiplicity. Therefore, we replace them with one root $x_(4)^(*)=-2$, but with a multiplicity of 1+1=2.

In addition, there are also identical roots: $((x)_(2))=-4$ and $x_(2)^(*)=-4$. They are also of the first multiplicity, so only $x_(2)^(*)=-4$ of multiplicity 1+1=2 remains.

Please note: in both cases, we left exactly the “cut out” root, and threw out the “painted over” one from consideration. Because even at the beginning of the lesson, we agreed: if a point is both punched out and painted over at the same time, then we still consider it punched out.

As a result, we have four roots, and all of them turned out to be gouged out:

\[\begin(align) & x_(1)^(*)=4; \\ & x_(2)^(*)=-4\left(2k \right); \\ & x_(3)^(*)=-7; \\ & x_(4)^(*)=-2\left(2k \right). \\ \end(align)\]

We mark them on the number line, taking into account the multiplicity:

We place the signs and paint over the areas of interest to us:

Everything. No isolated points and other perversions. You can write down the answer.

Answer. $x\in \left(-\infty ;-7 \right)\bigcup \left(4;+\infty \right)$.

multiplication rule

Sometimes an even more unpleasant situation occurs: an equation that has multiple roots is itself raised to a certain power. This changes the multiplicities of all the original roots.

This is rare, so most students do not have experience in solving such problems. And the rule here is:

When an equation is raised to a power $n$, the multiplicity of all its roots also increases by a factor of $n$.

In other words, raising to a power results in multiplying multiplicities by the same power. Let's take this rule as an example:

A task. Solve the inequality:

\[\frac(x((\left(((x)^(2))-6x+9 \right))^(2))((\left(x-4 \right))^(5)) )(((\left(2-x \right))^(3))((\left(x-1 \right))^(2)))\le 0\]

Decision. Set the numerator to zero:

The product is equal to zero when at least one of the factors is equal to zero. Everything is clear with the first multiplier: $x=0$. And here's where the problems start:

\[\begin(align) & ((\left(((x)^(2))-6x+9 \right))^(2))=0; \\ & ((x)^(2))-6x+9=0\left(2k \right); \\ & D=((6)^(3))-4\cdot 9=0 \\ & ((x)_(2))=3\left(2k \right)\left(2k \right) \ \ & ((x)_(2))=3\left(4k \right) \\ \end(align)\]

As you can see, the equation $((x)^(2))-6x+9=0$ has a unique root of the second multiplicity: $x=3$. The whole equation is then squared. Therefore, the multiplicity of the root will be $2\cdot 2=4$, which we finally wrote down.

\[((\left(x-4 \right))^(5))=0\Rightarrow x=4\left(5k \right)\]

No problem with the denominator either:

\[\begin(align) & ((\left(2-x \right))^(3))((\left(x-1 \right))^(2))=0; \\ & ((\left(2-x \right))^(3))=0\Rightarrow x_(1)^(*)=2\left(3k \right); \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(2)^(*)=1\left(2k \right). \\ \end(align)\]

In total, we got five points: two punched out and three filled in. There are no coinciding roots in the numerator and denominator, so we just mark them on the number line:

We arrange the signs taking into account the multiplicities and paint over the intervals of interest to us:
Again one isolated point and one punctured
Because of the roots of even multiplicity, we again received a couple of “non-standard” elements. This is $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)$, not $x\in \left[ 0;2 \right)$, and also an isolated point $ x\in \left$ 3 \right$$.

Answer. $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)\bigcup \left$ 3 \right$\bigcup \left[ 4;+\infty \right)$

As you can see, everything is not so difficult. The main thing is attentiveness. The last section of this lesson is devoted to transformations - the very ones that we discussed at the very beginning.

Preconversions

The inequalities we will discuss in this section are not complex. However, unlike the previous tasks, here you will have to apply skills from the theory of rational fractions - factorization and reduction to a common denominator.

We discussed this issue in detail at the very beginning of today's lesson. If you are not sure that you understand what it is about, I strongly recommend that you go back and repeat. Because there is no point in cramming the methods for solving inequalities if you "swim" in the conversion of fractions.

In homework, by the way, there will also be many similar tasks. They are placed in a separate subsection. And there you will find very non-trivial examples. But this will be in the homework, but now let's analyze a couple of such inequalities.

A task. Solve the inequality:

\[\frac(x)(x-1)\le \frac(x-2)(x)\]

Decision. Moving everything to the left:

\[\frac(x)(x-1)-\frac(x-2)(x)\le 0\]

We reduce to a common denominator, open the brackets, give like terms in the numerator:

\[\begin(align) & \frac(x\cdot x)(\left(x-1 \right)\cdot x)-\frac(\left(x-2 \right)\left(x-1 \ right))(x\cdot \left(x-1 \right))\le 0; \\ & \frac(((x)^(2))-\left(((x)^(2))-2x-x+2 \right))(x\left(x-1 \right)) \le0; \\ & \frac(((x)^(2))-((x)^(2))+3x-2)(x\left(x-1 \right))\le 0; \\ & \frac(3x-2)(x\left(x-1 \right))\le 0. \\\end(align)\]

Now we have a classical fractional rational inequality, the solution of which is no longer difficult. I propose to solve it by an alternative method - through the method of intervals:

\[\begin(align) & \left(3x-2 \right)\cdot x\cdot \left(x-1 \right)=0; \\ & ((x)_(1))=\frac(2)(3);\ ((x)_(2))=0;\ ((x)_(3))=1. \\ \end(align)\]

Don't forget the constraint that comes from the denominator:

We mark all the numbers and restrictions on the number line:

All roots have first multiplicity. No problem. We just place the signs and paint over the areas we need:

It's all. You can write down the answer.

Answer. $x\in \left(-\infty ;0 \right)\bigcup \left[ (2)/(3)\;;1 \right)$.

Of course, this was a very simple example. So now let's take a closer look at the problem. And by the way, the level of this task is quite consistent with independent and control work on this topic in the 8th grade.

A task. Solve the inequality:

\[\frac(1)(((x)^(2))+8x-9)\ge \frac(1)(3((x)^(2))-5x+2)\]

Decision. Moving everything to the left:

\[\frac(1)(((x)^(2))+8x-9)-\frac(1)(3((x)^(2))-5x+2)\ge 0\]

Before bringing both fractions to a common denominator, we decompose these denominators into factors. Suddenly the same brackets will come out? With the first denominator it's easy:

\[((x)^(2))+8x-9=\left(x-1 \right)\left(x+9 \right)\]

The second one is a little more difficult. Feel free to add a constant multiplier to the bracket where the fraction was found. Remember: the original polynomial had integer coefficients, so it is highly likely that the factorization will also have integer coefficients (in fact, it always will, except when the discriminant is irrational).

\[\begin(align) & 3((x)^(2))-5x+2=3\left(x-1 \right)\left(x-\frac(2)(3) \right)= \\ & =\left(x-1 \right)\left(3x-2 \right) \end(align)\]

As you can see, there is a common bracket: $\left(x-1 \right)$. We return to the inequality and bring both fractions to a common denominator:

\[\begin(align) & \frac(1)(\left(x-1 \right)\left(x+9 \right))-\frac(1)(\left(x-1 \right)\ left(3x-2\right))\ge 0; \\ & \frac(1\cdot \left(3x-2 \right)-1\cdot \left(x+9 \right))(\left(x-1 \right)\left(x+9 \right )\left(3x-2 \right))\ge 0; \\ & \frac(3x-2-x-9)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ & \frac(2x-11)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ \end(align)\]

Set the denominator to zero:

\[\begin(align) & \left(x-1 \right)\left(x+9 \right)\left(3x-2 \right)=0; \\ & x_(1)^(*)=1;\ x_(2)^(*)=-9;\ x_(3)^(*)=\frac(2)(3) \\ \end( align)\]

No multiplicities and no coinciding roots. We mark four numbers on a straight line:

We place the signs:

We write down the answer.

Answer: $x\in \left(-\infty ;-9 \right)\bigcup \left((2)/(3)\;;1 \right)\bigcup \left[ 5,5;+\infty \ right)$.

Everything! Like that, I read up to this line. :)

Linear inequalities are called the left and right parts of which are linear functions with respect to the unknown value. These include, for example, the inequalities:

2x-1-x+3; 7x0;

5 >4 - 6x 9- x< x + 5 .

1) Strict inequalities: ax+b>0 or ax+b<0

2) Non-strict inequalities: ax+b≤0 or ax+b≫ 0

Let's take this task. One side of a parallelogram is 7 cm. What should be the length of the other side so that the perimeter of the parallelogram is greater than 44 cm?

Let the desired side be X see In this case, the perimeter of the parallelogram will be represented by (14 + 2x) see. The inequality 14 + 2x > 44 is a mathematical model of the problem of the perimeter of a parallelogram. If in this inequality we replace the variable X on, for example, the number 16, then we get the correct numerical inequality 14 + 32\u003e 44. In this case, we say that the number 16 is the solution to the inequality 14 + 2x\u003e 44.

Inequality solution name the value of the variable that turns it into a true numerical inequality.

Therefore, each of the numbers 15.1; 20;73 act as a solution to the inequality 14 + 2x > 44, and the number 10, for example, is not its solution.

Solve the inequality means to establish all its solutions or to prove that solutions do not exist.

The formulation of the solution of the inequality is similar to the formulation of the root of the equation. And yet it is not customary to designate the "root of inequality."

The properties of numerical equalities helped us solve equations. Similarly, properties of numerical inequalities will help solve inequalities.

Solving the equation, we change it to another, simpler equation, but equivalent to the given one. In a similar way, the answer is found for inequalities. When changing the equation to an equation equivalent to it, they use the theorem on the transfer of terms from one part of the equation to the opposite and on the multiplication of both parts of the equation by the same non-zero number. When solving an inequality, there is a significant difference between it and an equation, which lies in the fact that any solution to an equation can be checked simply by substituting it into the original equation. In inequalities, there is no such method, since it is not possible to substitute an infinite number of solutions into the original inequality. Therefore, there is an important concept, these arrows<=>is the sign of equivalent, or equivalent, transformations. The transformation is called equivalent or equivalent if they do not change the decision set.

Similar rules for solving inequalities.

If any term is moved from one part of the inequality to another, while replacing its sign with the opposite one, then we obtain an inequality equivalent to the given one.

If both parts of the inequality are multiplied (divided) by the same positive number, then we obtain an inequality equivalent to the given one.

If both parts of the inequality are multiplied (divided) by the same negative number, while replacing the inequality sign with the opposite one, then we obtain an inequality equivalent to the given one.

Using these regulations we calculate the following inequalities.

1) Let's analyze the inequality 2x - 5 > 9.

This linear inequality, find its solution and discuss the basic concepts.

2x - 5 > 9<=>2x > 14(5 was moved to the left side with the opposite sign), then we divided everything by 2 and we have x > 7. We apply a set of solutions to the axis x

We have obtained a positively directed beam. We note the set of solutions either in the form of the inequality x > 7, or as an interval x(7; ∞). And what is a particular solution to this inequality? For example, x=10 is a particular solution to this inequality, x=12 is also a particular solution of this inequality.

There are many particular solutions, but our task is to find all solutions. And the solutions are usually infinite.

Let's analyze example 2:

2) Solve the inequality 4a - 11 > a + 13.

Let's solve it: a move to one side 11 move to the other side, we get 3a< 24, и в результате после деления обеих частей на 3 inequality has the form a<8 .

4a - 11 > a + 13<=>3a< 24 <=>a< 8 .

We will also display the set a< 8 , but already on the axis a.

The answer is either written as an inequality a< 8, либо a(-∞;8), 8 does not turn on.

Spacing Method is a simple way to solve fractional rational inequalities. This is the name of inequalities containing rational (or fractional-rational) expressions that depend on a variable.

1. Consider, for example, the following inequality

The interval method allows you to solve it in a couple of minutes.

On the left side of this inequality is a fractional rational function. Rational, because it contains neither roots, nor sines, nor logarithms - only rational expressions. On the right is zero.

The interval method is based on the following property of a fractional rational function.

A fractional rational function can change sign only at those points where it is equal to zero or does not exist.

Recall how a square trinomial is factored, that is, an expression of the form .

Where and are the roots of the quadratic equation.

We draw an axis and arrange the points at which the numerator and denominator vanish.

The zeros of the denominator and are punctured points, since at these points the function on the left side of the inequality is not defined (you cannot divide by zero). The zeros of the numerator and - are shaded because the inequality is not strict. For and our inequality is satisfied, since both its parts are equal to zero.

These points break the axis into intervals.

Let us determine the sign of the fractional-rational function on the left side of our inequality on each of these intervals. We remember that a fractional rational function can change sign only at those points where it is equal to zero or does not exist. This means that on each of the intervals between the points where the numerator or denominator vanishes, the sign of the expression on the left side of the inequality will be constant - either "plus" or "minus".

And therefore, to determine the sign of the function on each such interval, we take any point belonging to this interval. The one that suits us.
. Take, for example, and check the sign of the expression on the left side of the inequality. Each of the "brackets" is negative. The left side has a sign.

Next interval: . Let's check the sign for . We get that the left side has changed sign to .

Let's take . When the expression is positive - therefore, it is positive on the entire interval from to .

For , the left side of the inequality is negative.

And finally class="tex" alt="(!LANG:x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

We have found on what intervals the expression is positive. It remains to write the answer:

Answer: .

Please note: the signs on the intervals alternate. This happened because when passing through each point, exactly one of the linear factors changed sign, and the rest kept it unchanged.

We see that the interval method is very simple. To solve a fractional-rational inequality by the method of intervals, we bring it to the form:

Or class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle P\left(x \right))(\displaystyle Q\left(x \right)) > 0"> !}, or or .

(on the left side - a fractional-rational function, on the right side - zero).

Then - we mark on the number line the points at which the numerator or denominator vanishes.
These points divide the entire number line into intervals, on each of which the fractional-rational function retains its sign.
It remains only to find out its sign on each interval.
We do this by checking the sign of the expression at any point within the given interval. After that, we write down the answer. That's all.

But the question arises: do the signs always alternate? No not always! We must be careful not to place signs mechanically and thoughtlessly.

2. Let's look at another inequality.

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle \left(x-2 \right)^2)(\displaystyle \left(x-1 \right) \left(x-3\right))>0"> !}

We again place points on the axis. The points and are punctured because they are the zeros of the denominator. The dot is also punctured, since the inequality is strict.

When the numerator is positive, both factors in the denominator are negative. This is easy to check by taking any number from a given interval, for example, . The left side has the sign:

When the numerator is positive; the first factor in the denominator is positive, the second factor is negative. The left side has the sign:

When the situation is the same! The numerator is positive, the first factor in the denominator is positive, the second is negative. The left side has the sign:

Finally, with class="tex" alt="(!LANG:x>3"> все множители положительны, и левая часть имеет знак :!}

Answer: .

Why was the alternation of characters broken? Because when passing through the point, the multiplier "responsible" for it did not change sign. Consequently, the entire left-hand side of our inequality did not change sign either.

Output: if the linear factor is in an even power (for example, in a square), then when passing through a point, the sign of the expression on the left side does not change. In the case of an odd degree, the sign, of course, changes.

3. Let's consider a more complicated case. It differs from the previous one in that the inequality is not strict:

The left side is the same as in the previous problem. The picture of signs will be the same:

Maybe the answer will be the same? No! The solution is added This is because at , both the left and right sides of the inequality are equal to zero - therefore, this point is a solution.

Answer: .

In the problem on the exam in mathematics, this situation is often encountered. Here, applicants fall into a trap and lose points. Be careful!

4. What if the numerator or denominator cannot be factored into linear factors? Consider this inequality:

The square trinomial cannot be factorized: the discriminant is negative, there are no roots. But this is good! This means that the sign of the expression is the same for all, and specifically, it is positive. You can read more about this in the article on the properties of a quadratic function.

And now we can divide both sides of our inequality by a value that is positive for all . We arrive at an equivalent inequality:

Which is easily solved by the interval method.

Pay attention - we divided both sides of the inequality by the value, which we knew for sure that it was positive. Of course, in the general case, you should not multiply or divide an inequality by a variable whose sign is unknown.

5 . Consider another inequality, seemingly quite simple:

So I want to multiply it by . But we are already smart, and we will not do this. After all, it can be both positive and negative. And we know that if both parts of the inequality are multiplied by a negative value, the sign of the inequality changes.

We will act differently - we will collect everything in one part and bring it to a common denominator. Zero will remain on the right side:

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}

And after that - applicable interval method.

Solving inequalities online

Before solving inequalities, it is necessary to understand well how equations are solved.

It does not matter whether the inequality is strict () or non-strict (≤, ≥), the first step is to solve the equation by replacing the inequality sign with equality (=).

Explain what it means to solve an inequality?

After studying the equations, the student has the following picture in his head: you need to find such values of the variable for which both parts of the equation take the same values. In other words, find all points where the equality holds. Everything is correct!

When talking about inequalities, they mean finding the intervals (segments) on which the inequality holds. If there are two variables in the inequality, then the solution will no longer be intervals, but some areas on the plane. Guess what will be the solution of the inequality in three variables?

How to solve inequalities?

The method of intervals (aka the method of intervals) is considered to be a universal way to solve inequalities, which consists in determining all the intervals within which the given inequality will be fulfilled.

Without going into the type of inequality, in this case it is not the essence, it is required to solve the corresponding equation and determine its roots, followed by the designation of these solutions on the numerical axis.

What is the correct way to write the solution to an inequality?

When you have determined the intervals for solving the inequality, you need to correctly write out the solution itself. There is an important nuance - are the boundaries of the intervals included in the solution?

Everything is simple here. If the solution of the equation satisfies the ODZ and the inequality is not strict, then the boundary of the interval is included in the solution of the inequality. Otherwise, no.

Considering each interval, the solution to the inequality can be the interval itself, or a half-interval (when one of its boundaries satisfies the inequality), or a segment - an interval together with its boundaries.

Important point

Do not think that only intervals, half-intervals and segments can be the solution to an inequality. No, individual points can also be included in the solution.

For example, the inequality |x|≤0 has only one solution - point 0.

And the inequality |x|

What is the inequality calculator for?

The inequality calculator gives the correct final answer. In this case, in most cases, an illustration of a numerical axis or plane is given. You can see whether the boundaries of the intervals are included in the solution or not - the points are displayed filled or pierced.

Thanks to the online inequality calculator, you can check whether you have found the roots of the equation correctly, marked them on the number line and checked the inequality conditions on the intervals (and boundaries)?

If your answer differs from the answer of the calculator, then you definitely need to double-check your solution and identify the mistake made.

Help on Tele2, tariffs, questions