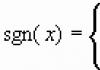Expressions, expression conversion

How to get rid of irrationality in the denominator? Ways, examples, solutions

In the 8th grade, in algebra lessons, within the framework of the topic of the transformation of irrational expressions, a conversation comes about liberation from irrationality in the denominator of a fraction. In this article, we will analyze what kind of transformation this is, consider what actions allow us to get rid of irrationality in the denominator of a fraction, and give solutions to typical examples with detailed explanations.

Page navigation.

What does it mean to get rid of irrationality in the denominator of a fraction?

First you need to figure out what irrationality is in the denominator and what it means to get rid of irrationality in the denominator of a fraction. Information from school textbooks will help us with this. The following points deserve attention.

When the fraction record contains the root sign (radical) in the denominator, then they say that the denominator contains irrationality. This is probably due to the fact that numbers written with root signs are often . As an example, let's take fractions , , , , obviously, the denominators of each of them contain the sign of the root, and hence the irrationality. In high school, a meeting with fractions is inevitable, the irrationality of the denominators of which is introduced not only by the signs of square roots, but also by the signs of cube roots, roots of the fourth degree, etc. Here are examples of such fractions: .

Considering the above information and the meaning of the word "liberate", the following definition is perceived very naturally:

Definition.

Exemption from irrationality in the denominator of a fraction- this is a transformation in which a fraction with irrationality in the denominator is replaced by an identically equal fraction that does not contain root signs in the denominator.

You can often hear that they say not to free themselves, but to get rid of the irrationality in the denominator of a fraction. The meaning does not change.

For example, if we move from a fraction to a fraction whose value is equal to the value of the original fraction and whose denominator does not contain the root sign, then we can state that we have freed ourselves from irrationality in the denominator of the fraction. Another example: replacing a fraction with an identically equal fraction there is a release from irrationality in the denominator of a fraction.

So, the initial information is received. It remains to find out what needs to be done to get rid of the irrationality in the denominator of the fraction.

Ways to free yourself from irrationality, examples

Usually, to get rid of irrationality in the denominator of a fraction, two fraction conversions: Multiply the numerator and denominator by a non-zero number or expression and convert the expression in the denominator. Below we will look at how these fraction transformations are used as part of the main ways to get rid of irrationality in the denominator of a fraction. Let's consider the following cases.

In the simplest cases, it is enough to transform the expression in the denominator. An example is a fraction whose denominator is the root of nine. In this case, replacing it with a value of 3 frees the denominator from being irrational.

In more complex cases, it is necessary to pre-multiply the numerator and denominator of the fraction by some non-zero number or expression, which subsequently allows you to convert the denominator of the fraction to a form that does not contain root signs. For example, after multiplying the numerator and denominator of a fraction by , the fraction becomes , and then the expression in the denominator can be replaced by the expression without signs of the roots x+1 . Thus, after liberation from irrationality in the denominator, the fraction takes the form .

If we talk about the general case, then in order to get rid of irrationality in the denominator of a fraction, one has to resort to various acceptable transformations, sometimes quite specific ones.

And now in detail.

Converting an expression to the denominator of a fraction

As already noted, one way to get rid of irrationality in the denominator of a fraction is to transform the denominator. Let's consider examples.

Example.

Get rid of irrationality in the denominator of a fraction .

Decision.

Expanding the brackets in the denominator, we arrive at the expression . Let's move on to fractions . Calculating the values ​​under the signs of the roots, we have . Obviously, in the resulting expression, it is possible, which gives a fraction, which is equal to 1/16. So we got rid of the irrationality in the denominator.

Usually the solution is written briefly without explanation, since the actions performed are quite simple:

Answer:

.

Example.

Decision.

When we talked about the transformation of irrational expressions using the properties of roots, we noted that for any expression A for even n (in our case n=2 ) the expression can be replaced by the expression |A| on the entire ODZ of variables for the original expression. Therefore, you can perform the following transformation of a given fraction: , which frees from irrationality in the denominator.

Answer:

.

Multiplying the numerator and denominator by the root

When the expression in the denominator of a fraction has the form , where the expression A does not contain root signs, then multiplying the numerator and denominator by lets get rid of irrationality in the denominator. This action is possible, since it does not vanish on the ODZ of the variables for the original expression. In this case, in the denominator, an expression is obtained that is easy to convert to the form without root signs: . We show the application of this approach with examples.

Example.

Get rid of irrationality in the denominator of the fraction: a), b).

Decision.

a) Multiplying the numerator and denominator of the fraction by the square root of three, we get .

b) To get rid of the square root sign in the denominator, we multiply the numerator and denominator of the fraction by , after which we perform transformations in the denominator:

Answer:

a), b) .

In the case when the denominator contains factors or , where m and n are some natural numbers, the numerator and denominator must be multiplied by such a factor so that after that the expression in the denominator can be converted to the form or , where k is some natural number, respectively. Then it is easy to pass to a fraction without irrationality in the denominator. We will show the application of the described method of getting rid of irrationality in the denominator using examples.

Example.

Get rid of irrationality in the denominator of a fraction: a), b).

Decision.

a) The nearest natural number greater than 3 and divisible by 5 is 5. In order for the indicator of the six to become equal to five, the expression in the denominator must be multiplied by. Consequently, the liberation from irrationality in the denominator of the fraction will be facilitated by the expression by which the numerator and denominator must be multiplied:

b) It is obvious that the nearest natural number that exceeds 15 and is divisible by 4 without remainder is 16. To get the exponent in the denominator became equal to 16, you need to multiply the expression located there by. Thus, multiplying the numerator and denominator of the original fraction by (note that the value of this expression is not equal to zero for which real x) will get rid of the irrationality in the denominator:

Answer:

a) , b) .

Multiplication by adjoint expression

The next way to get rid of irrationality in the denominator of a fraction covers cases where the denominator contains expressions of the form , , , , or . In these cases, in order to get rid of irrationality in the denominator of a fraction, it is necessary to multiply the numerator and denominator of the fraction by the so-called conjugate expression.

It remains to find out which expressions are conjugate for the above. For an expression, the adjoint expression is , and for an expression, the adjoint expression is . Similarly, for an expression, the conjugate is , and for an expression, the conjugate is . And for the expression, the conjugate is , and for the expression, the conjugate is . So, the expression conjugate to this expression differs from it in sign before the second term.

Let's see what the result of multiplying an expression by its conjugate expression. For example, consider the product . It can be replaced by the difference of squares, that is, from where you can go further to the expression a−b, which does not contain root signs.

Now it becomes clear how multiplying the numerator and denominator of a fraction by the expression conjugate to the denominator allows you to get rid of irrationality in the denominator of the fraction. Let us consider the solutions of typical examples.

Example.

Express the expression as a fraction, the denominator of which does not contain a radical: a), b).

Decision.

a) The expression conjugate to the denominator is . We multiply the numerator and denominator by it, which will allow us to get rid of irrationality in the denominator of the fraction:

b) For the expression, the conjugate is . Multiplying the numerator and denominator by it, we get

It was possible to first remove the minus sign from the denominator, and only after that multiply the numerator and denominator by the expression conjugate to the denominator:

Answer:

a) , b) .

Please note: when multiplying the numerator and denominator of a fraction by an expression with variables conjugate to the denominator, care must be taken that it does not vanish for any set of variable values ​​​​from the DPV for the original expression.

Example.

Get rid of irrationality in the denominator of a fraction.

Decision.

To begin with, let's find the area of ​​​​admissible values ​​​​(ODZ) of the variable x. It is determined by the conditions x≥0 and , from which we conclude that the ODZ is the set x≥0 .

The expression conjugate to the denominator is . We can multiply the numerator and denominator of the fraction by it, provided that , which on the ODZ is equivalent to the condition x≠16 . At the same time, we have

And for x=16 we have .

Thus, for all values ​​of the variable x from the ODZ, except for x=16 , , and for x=16 we have .

Answer:

Using the sum of cubes and difference of cubes formulas

From the previous paragraph, we learned that the multiplication of the numerator and denominator of a fraction by the expression conjugate to the denominator is carried out in order to further apply the difference of squares formula and thereby get rid of irrationality in the denominator. In some cases, other abbreviated multiplication formulas are also useful to get rid of irrationality in the denominator. For example, the formula for the difference of cubes a 3 −b 3 =(a−b) (a 2 +a b+b 2) allows you to get rid of irrationality when the denominator of a fraction contains expressions with cube roots of the form or , where A and B are some numbers or expressions. To do this, the numerator and denominator of the fraction are multiplied by the incomplete square of the sum or difference, respectively. The sum of cubes formula is similarly tried on a 3 +b 3 =(a+b) (a 2 −a b+b 2).

Example.

Get rid of irrationality in the denominator of a fraction: a), b) .

Decision.

a) It is easy to guess that in this case, getting rid of irrationality in the denominator allows multiplying the numerator and denominator by an incomplete square of the sum of numbers and , since in the future this will allow us to transform the expression in the denominator according to the formula difference of cubes:

b) Expression in the denominator of a fraction can be represented as , from which it is clearly seen that this is an incomplete square of the difference between the numbers 2 and . Thus, if the numerator and denominator of the fraction are multiplied by the sum, then the denominator can be converted according to the formula sum of cubes, which will allow you to get rid of irrationality in the denominator of the fraction. This can be done under the condition , which is equivalent to the condition and further x≠−8 :

And when substituting x=−8 into the original fraction, we have .

Thus, for all x from the ODZ for the original fraction (in this case, this is the set R ), except for x=−8 , we have , and for x=8 we have .

Answer:

Using different methods

In more complicated examples, it usually does not work out in one action to get rid of the irrationality in the denominator, but you have to consistently apply method after method, including those discussed above. Sometimes some non-standard solutions may be required. Quite interesting tasks on the topic under discussion can be found in the textbook authored by Yu. N. Kolyagin. Bibliography.

1. Algebra: textbook for 8 cells. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; ed. S. A. Telyakovsky. - 16th ed. - M. : Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
2. Mordkovich A. G. Algebra. 8th grade. At 2 pm Part 1. A textbook for students of educational institutions / A. G. Mordkovich. - 11th ed., erased. - M.: Mnemozina, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.
3. Algebra and the beginning of mathematical analysis. Grade 10: textbook. for general education institutions: basic and profile. levels / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; ed. A. B. Zhizhchenko. - 3rd ed. - M.: Enlightenment, 2010.- 368 p. : Ill. - ISBN 978-5-09-022771-1.

Danny Peric Campana

Another interesting book for schoolchildren who are interested, unfortunately not translated into Russian, is the book “Daniel’s Mathematical Adventures” (Las Aventuras Matemáticas de Daniel) by the Chilean mathematics teacher Danny Perich Campana, a very extraordinary and interesting person . He not only teaches children, but also writes songs, puts various teaching materials on mathematics on the Internet. They can be found on youtube and on the site http://www.sectormatematica.cl/ (of course, all materials are in Spanish).

Here I post one chapter from the book by Danny Peric. It seemed to me quite interesting and useful for schoolchildren. To make it clear what we are talking about, I will say that Daniel and Camila work at a school, they are teachers.

The secret of getting rid of irrationality

“Camila, I now have a lot of problems when I try to explain what is being used for what we are going through in the lesson,” said Daniel.

“I don't really understand what you're talking about.

- I'm talking about what is in all school textbooks and even books at the university level. I still have no doubts: why do we need to get rid of irrationality in the denominator? And I hate to tell what I don’t understand for so long, complained Daniel.

“I also don’t know where it comes from and why it is needed, but there must be some logical explanation for this.

- Once I read in one scientific journal that getting rid of the irrationality in the denominator allows you to get a result with greater accuracy, but I have never seen this again and I'm not sure that this is the case.

Why don't we check it out? Camila asked.

"You're right," Daniel agreed. “Instead of complaining, you should try to draw your own conclusions. Then help me...

“Of course, now I’m interested in it myself.

“We should take some expressions and get rid of the irrationality in the denominator, then replace the root with its value and find the result of the expression before and after getting rid of the irrationality in the denominator and see if anything changes.

“Of course,” Camila agreed. - Let's do that.

“Take, for example, the expression,” Daniel said and took a sheet of paper to write down what was happening. - Multiply the numerator and denominator by and get .

“It will be correct and may help us to draw conclusions if we consider other irrational expressions equal to this one,” Camila suggested.

- I agree, - said Daniel, - I will divide the numerator and denominator by , and you multiply them by .

- I managed . And you have?

“I have,” Daniel replied. - Now we calculate the original expression and the resulting ones, replacing it with its value with all the decimal places that the calculator gives. We get:

"I don't see anything out of the ordinary," Camila said. “I was expecting some kind of difference that would justify getting rid of irrationality.

“As I told you, I once read about it in connection with the approach. What would you say if we changed to a less precise number, like ?

Let's try and see what happens.

Solving equations with fractions let's look at examples. The examples are simple and illustrative. With their help, you can understand in the most understandable way,.
For example, you need to solve a simple equation x/b + c = d.

An equation of this type is called linear, because the denominator contains only numbers.

The solution is performed by multiplying both sides of the equation by b, then the equation takes the form x = b*(d – c), i.e. the denominator of the fraction on the left side is reduced.

For example, how to solve a fractional equation:
x/5+4=9
We multiply both parts by 5. We get:
x+20=45
x=45-20=25

Another example where the unknown is in the denominator:

Equations of this type are called fractional rational or simply fractional.

We would solve a fractional equation by getting rid of fractions, after which this equation, most often, turns into a linear or quadratic one, which is solved in the usual way. You should only take into account the following points:

• the value of a variable that turns the denominator to 0 cannot be a root;
• you cannot divide or multiply the equation by the expression =0.

Here comes into force such a concept as the area of ​​​​permissible values ​​​​(ODZ) - these are the values ​​\u200b\u200bof the roots of the equation for which the equation makes sense.

Thus, solving the equation, it is necessary to find the roots, and then check them for compliance with the ODZ. Those roots that do not correspond to our DHS are excluded from the answer.

For example, you need to solve a fractional equation:

Based on the above rule, x cannot be = 0, i.e. ODZ in this case: x - any value other than zero.

We get rid of the denominator by multiplying all terms of the equation by x

And solve the usual equation

5x - 2x = 1
3x=1
x = 1/3

Answer: x = 1/3

Let's solve the equation more complicated:

ODZ is also present here: x -2.

Solving this equation, we will not transfer everything in one direction and bring fractions to a common denominator. We immediately multiply both sides of the equation by an expression that will reduce all the denominators at once.

To reduce the denominators, you need to multiply the left side by x + 2, and the right side by 2. So, both sides of the equation must be multiplied by 2 (x + 2):

This is the most common multiplication of fractions, which we have already discussed above.

We write the same equation, but in a slightly different way.

The left side is reduced by (x + 2), and the right side by 2. After the reduction, we get the usual linear equation:

x \u003d 4 - 2 \u003d 2, which corresponds to our ODZ

Answer: x = 2.

Solving equations with fractions not as difficult as it might seem. In this article, we have shown this with examples. If you are having any difficulty with how to solve equations with fractions, then unsubscribe in the comments.

In this topic, we will consider all three of the above groups of limits with irrationality. Let's start with limits containing an uncertainty of the form $\frac(0)(0)$.

Uncertainty disclosure $\frac(0)(0)$.

The scheme for solving standard examples of this type usually consists of two steps:

• We get rid of the irrationality that caused the uncertainty by multiplying by the so-called "adjoint" expression;
• If necessary, we decompose the expression in the numerator or denominator (or both) into factors;
• We reduce the factors that lead to uncertainty and calculate the desired value of the limit.

The term "adjoint expression" used above will be explained in detail in the examples. So far, there is no reason to dwell on it in detail. In general, you can go the other way, without using the conjugate expression. Sometimes a well-chosen replacement can get rid of irrationality. Such examples are rare in standard tests, so we will consider only one example No. 6 to use the replacement (see the second part of this topic).

We will need a few formulas, which I will write down below:

\begin(equation) a^2-b^2=(a-b)\cdot(a+b) \end(equation) \begin(equation) a^3-b^3=(a-b)\cdot(a^2 +ab+b^2) \end(equation) \begin(equation) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(equation) \begin (equation) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(equation)

In addition, we assume that the reader knows the formulas for solving quadratic equations. If $x_1$ and $x_2$ are the roots of the square trinomial $ax^2+bx+c$, then it can be factorized using the following formula:

\begin(equation) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(equation)

Formulas (1)-(5) are quite enough to solve standard problems, to which we now turn.

Example #1

Find $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$.

Since $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ and $\lim_(x\ to 3) (x-3)=3-3=0$, then in the given limit we have an uncertainty of the form $\frac(0)(0)$. The difference $\sqrt(7-x)-2$ prevents us from revealing this uncertainty. In order to get rid of such irrationalities, multiplication by the so-called "adjoint expression" is used. We will now consider how such multiplication works. Multiply $\sqrt(7-x)-2$ by $\sqrt(7-x)+2$:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

To expand the brackets, we apply , substituting $a=\sqrt(7-x)$, $b=2$ into the right side of the mentioned formula:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

As you can see, if you multiply the numerator by $\sqrt(7-x)+2$, then the root (i.e. irrationality) in the numerator disappears. This expression $\sqrt(7-x)+2$ will be conjugate to the expression $\sqrt(7-x)-2$. However, we cannot simply take and multiply the numerator by $\sqrt(7-x)+2$, because this will change the fraction $\frac(\sqrt(7-x)-2)(x-3)$, which is under the limit . You need to multiply both the numerator and the denominator at the same time:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \left|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Now remember that $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ and expand the brackets. And after opening the brackets and a little transformation $3-x=-(x-3)$, we reduce the fraction by $x-3$:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\to 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\to 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\to 3)\frac(-1 )(\sqrt(7-x)+2) $$

The uncertainty $\frac(0)(0)$ is gone. Now you can easily get the answer of this example:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

I note that the conjugate expression can change its structure - depending on what kind of irrationality it should remove. In examples #4 and #5 (see the second part of this topic), a different kind of conjugate expression will be used.

Answer: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

Example #2

Find $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$.

Since $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^2-19)=3-3=0$ and $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, then we we are dealing with an uncertainty of the form $\frac(0)(0)$. Let's get rid of irrationality in the denominator of this fraction. To do this, let's add both the numerator and denominator of the fraction $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ to the expression $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ conjugate to the denominator:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\left|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Again, as in example No. 1, you need to use parentheses to expand. Substituting $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$ into the right side of the mentioned formula, we get the following expression for the denominator:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ right)=\\ =\left(\sqrt(x^2+5)\right)^2-\left(\sqrt(7x^2-19)\right)^2=x^2+5-(7x ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Let's go back to our limit:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))((\sqrt(x ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19)))= \lim_(x\to 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

In example No. 1, almost immediately after multiplying by the conjugate expression, the fraction was reduced. Here, before the reduction, it is necessary to factorize the expressions $3x^2-5x-2$ and $x^2-4$, and only then proceed to the reduction. To factorize the expression $3x^2-5x-2$ you need to use . First, let's solve the quadratic equation $3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(aligned) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(aligned) $$

Substituting $x_1=-\frac(1)(3)$, $x_2=2$ into , we have:

$$ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)(x-2)=3\cdot\left(x+\ frac(1)(3)\right)(x-2)=\left(3\cdot x+3\cdot\frac(1)(3)\right)(x-2) =(3x+1)( x-2). $$

Now it's time to factor out the expression $x^2-4$. Let's use , substituting $a=x$, $b=2$ into it:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Let's use the obtained results. Since $x^2-4=(x-2)(x+2)$ and $3x^2-5x-2=(3x+1)(x-2)$, then:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2 -19)))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

Reducing by bracket $x-2$ we get:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^ 2-19)))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

Everything! The uncertainty is gone. One more step and we come to the answer:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2 ^2-19)))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Answer: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4)$.

In the following example, consider the case when irrationality will be present both in the numerator and in the denominator of a fraction.

Example #3

Find $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))$.

Since $\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ and $\lim_( x\to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, then we have an uncertainty of the form $\frac (0)(0)$. Since in this case the roots are present both in the denominator and in the numerator, in order to get rid of the uncertainty, you will have to multiply by two brackets at once. First, to the expression $\sqrt(x+4)+\sqrt(x^2-16)$ conjugate to the numerator. And secondly, to the expression $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ conjugate to the denominator.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=\left|\frac(0)(0)\right|=\\ =\lim_(x\to 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((\sqrt(x^2 -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2 -16))) $$ $$ -x^2+x+20=0;\\ \begin(aligned) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(aligned) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

For the expression $x^2-8x+15$ we get:

$$ x^2-8x+15=0;\\ \begin(aligned) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(- 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10)(2)=5. \end(aligned)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Substituting the obtained expansions $-x^2+x+20=-(x-5)(x+4)$ and $x^2+8x+15=(x-3)(x-5)$ into the considered limit, will have:

$$ \lim_(x\to 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x^2 -8x+15)(\sqrt(x+4)+\sqrt(x^2-16)))= \lim_(x\to 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\to 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3) (\sqrt(x+4)+\sqrt(x^2-16)))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5 \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Answer: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=-6$.

In the next (second) part, we will consider a couple more examples in which the conjugate expression will have a different form than in the previous problems. The main thing to remember is that the purpose of using a conjugate expression is to get rid of the irrationality that causes uncertainty.

When studying the transformations of an irrational expression, the question of how to get rid of irrationality in the denominator of a fraction is very important. The purpose of this article is to explain this action with specific task examples. In the first paragraph, we will consider the basic rules of this transformation, and in the second - characteristic examples with detailed explanations.

The concept of liberation from irrationality in the denominator

Let's start with an explanation of what the meaning of such a transformation is in general. For this, we recall the following provisions.

We can talk about irrationality in the denominator of a fraction if there is a radical present there, which is also the sign of the root. Numbers written with this sign are often irrational. Examples would be 1 2 , - 2 x + 3 , x + y x - 2 · x · y + 1 , 11 7 - 5 . Fractions with irrational denominators also include those that have roots of various degrees there (square, cubic, etc.), for example, 3 4 3, 1 x + x y 4 + y. To get rid of irrationality should be to simplify the expression and facilitate further calculations. Let us formulate the main definition:

Definition 1

Get rid of irrationality in the denominator of a fraction- means to transform it, replacing it with an identically equal fraction, the denominator of which does not contain roots and degrees.

Such an action can be called liberation or getting rid of irrationality, while the meaning remains the same. Thus, the transition from 1 2 to 2 2 , i.e. to a fraction with an equal value without a root sign in the denominator and will be the action we need. Let's give another example: we have a fraction x x - y . Let's carry out the necessary transformations and get the fraction x · x + y x - y that is identically equal to it, freeing ourselves from irrationality in the denominator.

After formulating the definition, we can proceed directly to the study of the sequence of actions that need to be performed for such a transformation.

Basic steps to get rid of irrationality in the denominator of a fraction

To get rid of the roots, you need to carry out two successive fraction transformations: multiply both parts of the fraction by a number other than zero, and then transform the expression obtained in the denominator. Let's consider the main cases.

In the simplest case, you can get by with the transformation of the denominator. For example, we can take a fraction with a denominator equal to the root of 9. Having calculated 9, we write 3 in the denominator and thus get rid of irrationality.

However, much more often you have to pre-multiply the numerator and denominator by a number that will then allow you to bring the denominator to the desired form (without roots). So, if we multiply 1 x + 1 by x + 1 , we get the fraction x + 1 x + 1 x + 1 and we can replace the expression in its denominator with x + 1 . So we converted 1 x + 1 to x + 1 x + 1 , getting rid of the irrationality.

Sometimes the transformations to be performed are quite specific. Let's look at a few illustrative examples.

How to convert an expression to the denominator of a fraction

As we said, the simplest thing to do is to convert the denominator.

Example 1

Condition: free the fraction 1 2 18 + 50 from irrationality in the denominator.

Decision

To begin with, let's open the brackets and get the expression 1 2 18 + 2 50 . Using the basic properties of the roots, let's move on to the expression 1 2 · 18 + 2 · 50 . We calculate the values ​​of both expressions under the roots and get 1 36 + 100 . Here you can already extract the roots. As a result, we got a fraction 1 6 + 10, equal to 1 16. This completes the transformation.

We write down the course of the entire solution without comments:

1 2 18 + 50 = 1 2 18 + 2 50 = = 1 2 18 + 2 50 = 1 36 + 100 = 1 6 + 10 = 1 16

Answer: 1 2 18 + 50 = 1 16 .

Example 2

Condition: given a fraction 7 - x (x + 1) 2 . Get rid of the irrationality in the denominator.

Decision

Earlier in the article on transformations of irrational expressions using the properties of roots, we mentioned that for any A and even n, we can replace the expression A n n with | A | on the entire range of admissible values ​​of variables. Therefore, in our case, we can write it like this: 7 - x x + 1 2 = 7 - x x + 1. In this way, we freed ourselves from the irrationality in the denominator.

Answer: 7 - x x + 1 2 = 7 - x x + 1 .

Getting rid of irrationality by multiplying by the root

If the denominator of the fraction contains an expression of the form A and the expression A itself does not have root signs, then we can get rid of irrationality by simply multiplying both parts of the original fraction by A. The possibility of this action is determined by the fact that A on the range of valid values ​​will not turn into 0 . After multiplication, the denominator will contain an expression of the form A · A, which is easy to get rid of the roots: A · A \u003d A 2 \u003d A. Let's see how to apply this method in practice.

Example 3

Condition: fractions x 3 and - 1 x 2 + y - 4 are given. Get rid of the irrationality in their denominators.

Decision

Let's multiply the first fraction by the second root of 3. We get the following:

x 3 = x 3 3 3 = x 3 3 2 = x 3 3

In the second case, we need to multiply by x 2 + y - 4 and transform the resulting expression in the denominator:

1 x 2 + y - 4 = - 1 x 2 + y - 4 x 2 + y - 4 x 2 + y - 4 = = - x 2 + y - 4 x 2 + y - 4 2 = - x 2 + y - 4 x 2 + y - 4

Answer: x 3 = x 3 3 and - 1 x 2 + y - 4 = - x 2 + y - 4 x 2 + y - 4 .

If the denominator of the original fraction contains expressions of the form A n m or A m n (assuming m and n are natural), we need to choose a factor so that the resulting expression can be converted to A n n k or A n k n (if k is natural) . After that, getting rid of irrationality will not be difficult. Let's take an example.

Example 4

Condition: given fractions 7 6 3 5 and x x 2 + 1 4 15 . Get rid of the irrationality in the denominators.

Decision

We need to take a natural number that can be divided by five, while it must be greater than three. To make the exponent 6 equal to 5, we need to multiply by 6 2 5. Therefore, we will have to multiply both parts of the original fraction by 6 2 5:

7 6 3 5 = 7 6 2 5 6 3 5 6 2 5 = 7 6 2 5 6 3 5 6 2 = 7 6 2 5 6 5 5 = = 7 6 2 5 6 = 7 36 5 6

In the second case, we need a number greater than 15, which can be divided by 4 without a remainder. We take 16 . To get such an exponent in the denominator, we need to take x 2 + 1 4 as a factor. Let's clarify that the value of this expression will not be 0 in any case. We calculate:

x x 2 + 1 4 15 = x x 2 + 1 4 x 2 + 1 4 15 x 2 + 1 4 = = x x 2 + 1 4 x 2 + 1 4 16 = x x 2 + 1 4 x 2 + 1 4 4 4 = x x 2 + 1 4 x 2 + 1 4

Answer: 7 6 3 5 = 7 36 5 6 and x x 2 + 1 4 15 = x x 2 + 1 4 x 2 + 1 4 .

Getting rid of irrationality by multiplying by an adjoint expression

The following method is suitable for those cases when the denominator of the original fraction contains the expressions a + b, a - b, a + b, a - b, a + b, a - b. In such cases, we need to take the adjoint expression as a factor. Let us explain the meaning of this concept.

For the first expression a + b, the conjugate will be a - b, for the second a - b - a + b. For a + b - a - b, for a - b - a + b, for a + b - a - b, and for a - b - a + b. In other words, a conjugate expression is an expression in which the opposite sign is in front of the second term.

Let's take a look at what exactly this method is. Let's say we have a product of the form a - b · a + b . It can be replaced by the square difference a - b · a + b = a 2 - b 2 , after which we pass to the expression a − b without radicals. Thus, we got rid of the irrationality in the denominator of the fraction by multiplying by the conjugate expression. Let's take a couple of illustrative examples.

Example 5

Condition: get rid of the irrationality in the expressions 3 7 - 3 and x - 5 - 2 .

Decision

In the first case, we take the conjugate expression equal to 7 + 3. Now we multiply both parts of the original fraction by it:

3 7 - 3 = 3 7 + 3 7 - 3 7 + 3 = 3 7 + 3 7 2 - 3 2 = = 3 7 + 3 7 - 9 = 3 7 + 3 - 2 = - 3 7 + 3 2

In the second case, we need the expression - 5 + 2 , which is the conjugate of the expression - 5 - 2 . Multiply the numerator and denominator by it and get:

x - 5 - 2 = x - 5 + 2 - 5 - 2 - 5 + 2 = = x - 5 + 2 - 5 2 - 2 2 = x - 5 + 2 5 - 2 = x 2 - 5 3

It is also possible to perform a transformation before multiplication: if we remove the minus from the denominator first, it will be more convenient to count:

x - 5 - 2 = - x 5 + 2 = - x 5 - 2 5 + 2 5 - 2 = = - x 5 - 2 5 2 - 2 2 = - x 5 - 2 5 - 2 = - x 5 - 2 3 = = x 2 - 5 3

Answer: 3 7 - 3 = - 3 7 + 3 2 and x - 5 - 2 = x 2 - 5 3 .

It is important to pay attention to the fact that the expression obtained as a result of multiplication does not turn to 0 for any variables from the range of valid values ​​for this expression.

Example 6

Condition: given a fraction x x + 4 . Transform it so that there are no irrational expressions in the denominator.

Decision

Let's start by finding the range of valid values ​​for x . It is defined by the conditions x ≥ 0 and x + 4 ≠ 0 . From them, we can conclude that the desired area is a set x ≥ 0 .

The conjugate of the denominator is x - 4 . When can we perform multiplication on it? Only if x - 4 ≠ 0 . On the range of acceptable values, this will be equivalent to the condition x≠16. As a result, we will get the following:

x x + 4 = x x - 4 x + 4 x - 4 = = x x - 4 x 2 - 4 2 = x x - 4 x - 16

If x is equal to 16 , then we get:

x x + 4 = 16 16 + 4 = 16 4 + 4 = 2

Therefore, x x + 4 = x · x - 4 x - 16 for all values ​​of x that belong to the range of valid values, except for 16 . For x = 16 we get x x + 4 = 2 .

Answer: x x + 4 = x x - 4 x - 16 , x ∈ [ 0 , 16) ∪ (16 , + ∞) 2 , x = 16 .

Converting fractions with irrationality in the denominator using the formulas for the sum and difference of cubes

In the previous paragraph, we performed multiplication by conjugate expressions in order to then use the difference of squares formula. Sometimes, to get rid of irrationality in the denominator, it is useful to use other abbreviated multiplication formulas, for example, the difference of cubes a 3 - b 3 \u003d (a - b) (a 2 + a b + b 2). This formula is convenient to use if the denominator of the original fraction contains expressions with third-degree roots of the form A 3 - B 3 , A 3 2 + A 3 · B 3 + B 3 2 . etc. To apply it, we need to multiply the denominator of the fraction by the incomplete square of the sum A 3 2 + A 3 · B 3 + B 3 2 or the difference A 3 - B 3 . Similarly, you can apply the sum formula a 3 + b 3 \u003d (a) (a 2 - a b + b 2).

Example 7

Condition: transform the fractions 1 7 3 - 2 3 and 3 4 - 2 · x 3 + x 2 3 so as to get rid of the irrationality in the denominator.

Decision

For the first fraction, we need to use the method of multiplying both parts by the incomplete square of the sum of 7 3 and 2 3, because then we can perform the transformation using the cube difference formula:

1 7 3 - 2 3 = 1 7 3 2 + 7 3 2 3 + 2 3 2 7 3 - 2 3 7 3 2 + 7 3 2 3 + 2 3 2 = = 7 3 2 + 7 3 2 3 + 2 3 2 7 3 3 - 2 3 3 = 7 2 3 + 7 2 3 + 2 2 3 7 - 2 = = 49 3 + 14 3 + 4 3 5

In the second fraction, we represent the denominator as 2 2 - 2 · x 3 + x 3 2 . In this expression, the incomplete square of the difference 2 and x 3 is visible, which means that we can multiply both parts of the fraction by the sum 2 + x 3 and use the formula for the sum of cubes. For this, the condition 2 + x 3 ≠ 0 must be met, which is equivalent to x 3 ≠ - 2 and x ≠ - 8:

3 4 - 2 x 3 + x 2 3 = 3 2 2 - 2 x 3 + x 3 2 = = 3 2 + x 3 2 2 - 2 x 3 + x 3 2 2 + x 3 = 6 + 3 x 3 2 3 + x 3 3 = = 6 + 3 x 3 8 + x

Substitute in a fraction - 8 and find the value:

3 4 - 2 8 3 + 8 2 3 = 3 4 - 2 2 + 4 = 3 4

Let's summarize. For all x included in the range of the original fraction (set R), with the exception of - 8 , we get 3 4 - 2 x 3 + x 2 3 = 6 + 3 x 3 8 + x . If x = 8 , then 3 4 - 2 x 3 + x 2 3 = 3 4 .

Answer: 3 4 - 2 x 3 + x 2 3 \u003d 6 + 3 x 3 8 + x, x ≠ 8 3 4, x \u003d - 8.

Consistent application of various transformation methods

Often in practice there are more complex examples when we cannot get rid of the irrationality in the denominator using just one method. For them, you need to sequentially perform several transformations or select non-standard solutions. Let's take one such problem.

Example N

Condition: convert 5 7 4 - 2 4 to get rid of the root signs in the denominator.

Decision

Let's multiply both parts of the original fraction by the conjugate expression 7 4 + 2 4 with a non-zero value. We get the following:

5 7 4 - 2 4 = 5 7 4 + 2 4 7 4 - 2 4 7 4 + 2 4 = = 5 7 4 + 2 4 7 4 2 - 2 4 2 = 5 7 4 + 2 4 7 - 2

And now we apply the same method again:

5 7 4 + 2 4 7 - 2 = 5 7 4 + 2 4 7 + 2 7 - 2 7 + 2 = = 5 7 4 + 2 4 7 + 2 7 2 - 2 2 = 5 7 4 + 7 4 7 + 2 7 - 2 = = 5 7 4 + 2 4 7 + 2 5 = 7 4 + 2 4 7 + 2

Answer: 5 7 4 - 2 4 = 7 4 + 2 4 7 + 2 .

If you notice a mistake in the text, please highlight it and press Ctrl+Enter