Выпуклость функции. Направление выпуклости

Понятие выпуклости функции

Рассмотрим функцию \(y = f\left(x \right),\) которая предполагается непрерывной на отрезке \(\left[ {a,b} \right].\) Функция \(y = f\left(x \right)\) называется выпуклой вниз (или просто выпуклой ), если для любых точек \({x_1}\) и \({x_2}\) из \(\left[ {a,b} \right]\) выполняется неравенство \ Если данное неравенство является строгим при любых \({x_1},{x_2} \in \left[ {a,b} \right],\) таких, что \({x_1} \ne {x_2},\) то функцию \(f\left(x \right)\) называют строго выпуклой вниз

Аналогично определяется выпуклая вверх функция. Функция \(f\left(x \right)\) называется выпуклой вверх (или вогнутой ), если для любых точек \({x_1}\) и \({x_2}\) отрезка \(\left[ {a,b} \right]\) справедливо неравенство \ Если это неравенство является строгим при любых \({x_1},{x_2} \in \left[ {a,b} \right],\) таких, что \({x_1} \ne {x_2},\) то функцию \(f\left(x \right)\) называют строго выпуклой вверх на отрезке \(\left[ {a,b} \right].\)

Геометрическая интерпретация выпуклости функции

Введенные определения выпуклой функции имеют простую геометрическую интерпретацию.

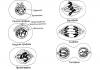
Для функции, выпуклой вниз (рисунок \(1\)), середина \(B\) любой хорды \({A_1}{A_2}\) лежит выше

Аналогично, для функции, выпуклой вверх (рисунок \(2\)), середина \(B\) любой хорды \({A_1}{A_2}\) лежит ниже соответствующей точки \({A_0}\) графика функции или совпадает с этой точкой.

Выпуклые функции обладают еще одним наглядным свойством, которое связано с расположением касательной к графику функции. Функция \(f\left(x \right)\) является выпуклой вниз на отрезке \(\left[ {a,b} \right]\) тогда и только тогда, когда ее график лежит не ниже касательной проведенной к нему в любой точке \({x_0}\) отрезка \(\left[ {a,b} \right]\) (рисунок \(3\)).

Соответственно, функция \(f\left(x \right)\) является выпуклой вверх на отрезке \(\left[ {a,b} \right]\) тогда и только тогда, когда ее график лежит не выше касательной проведенной к нему в любой точке \({x_0}\) отрезка \(\left[ {a,b} \right]\) (рисунок \(4\)). Данные свойства представляют собой теорему и могут быть доказаны с использованием определения выпуклости функции.

Достаточные условия выпуклости

Пусть для функции \(f\left(x \right)\) первая производная \(f"\left(x \right)\) существует на отрезке \(\left[ {a,b} \right],\) а вторая производная \(f""\left(x \right)\) − на интервале \(\left({a,b} \right).\) Тогда справедливы следующие достаточные признаки выпуклости:

Если \(f""\left(x \right) \ge 0\) при всех \(x \in \left({a,b} \right),\) то функция \(f\left(x \right)\) выпукла вниз на отрезке \(\left[ {a,b} \right];\)

Если \(f""\left(x \right) \le 0\) при всех \(x \in \left({a,b} \right),\) то функция \(f\left(x \right)\) выпукла вверх на отрезке \(\left[ {a,b} \right].\)

В тех случаях, когда вторая производная строго больше (меньше) нуля, говорят, соответственно, о строгой выпуклости вниз (или вверх ).

Докажем приведенную теорему для случая выпуклой вниз функции. Пусть функция \(f\left(x \right)\) имеет неотрицательную вторую производную на интервале \(\left({a,b} \right):\) \(f""\left(x \right) \ge 0.\) Обозначим через \({x_0}\) середину отрезка \(\left[ {{x_1},{x_2}} \right].\) Предположим, что длина этого отрезка равна \(2h.\) Тогда координаты \({x_1}\) и \({x_2}\) можно записать в виде: \[{x_1} = {x_0} - h,\;\;{x_2} = {x_0} + h.\] Разложим функцию \(f\left(x \right)\) в точке \({x_0}\) в ряд Тейлора с остаточным членом в форме Лагранжа. Получаем следующие выражения: \[ {f\left({{x_1}} \right) = f\left({{x_0} - h} \right) } = {f\left({{x_0}} \right) - f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _1}} \right){h^2}}}{{2!}},} \] \[ {f\left({{x_2}} \right) = f\left({{x_0} + h} \right) } = {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},} \] где \({x_0} - h
Сложим оба равенства: \[ {f\left({{x_1}} \right) + f\left({{x_2}} \right) } = {2f\left({{x_0}} \right) + \frac{{{h^2}}}{2}\left[ {f""\left({{\xi _1}} \right) + f""\left({{\xi _2}} \right)} \right].} \] Поскольку \({\xi _1},{\xi _2} \in \left({a,b} \right),\) то вторые производные в правой части неотрицательны. Следовательно, \ или \ то есть, в соответствии с определением, функция \(f\left(x \right)\) выпукла вниз .

Отметим, что необходимое условие выпуклости функции (т.е. прямая теорема, в которой, к примеру, из условия выпуклости вниз следует, что \(f""\left(x \right) \ge 0\)) выполняется лишь для нестрогого неравенства. В случае строгой выпуклости необходимое условие, вообще говоря, не соблюдается. Например, функция \(f\left(x \right) = {x^4}\) является строго выпуклой вниз. Однако в точке \(x = 0\) ее вторая производная равна нулю, т.е. строгое неравенство \(f""\left(x \right) \gt 0\) в этом случае не выполняется.

Свойства выпуклых функций

Перечислим некоторые свойства выпуклых функций, предполагая, что все функции определены и непрерывны на отрезке \(\left[ {a,b} \right].\)

Если функции \(f\) и \(g\) выпуклы вниз (вверх), то любая их линейная комбинация \(af + bg,\) где \(a\), \(b\) − положительные действительные числа, также выпукла вниз (вверх).

Если функция \(u = g\left(x \right)\) выпукла вниз, а функция \(y = f\left(u \right)\) является выпуклой вниз и неубывающей, то сложная функция \(y = f\left({g\left(x \right)} \right)\) будет также выпуклой вниз.

Если функция \(u = g\left(x \right)\) выпукла вверх, а функция \(y = f\left(u \right)\) является выпуклой вниз и невозрастающей, то сложная функция \(y = f\left({g\left(x \right)} \right)\) будет выпуклой вниз.

Локальный максимум выпуклой вверх функции, заданной на отрезке \(\left[ {a,b} \right],\) является одновременно ее наибольшим значением на этом отрезке.

Локальный минимум выпуклой вниз функции, заданной на отрезке \(\left[ {a,b} \right],\) является одновременно ее наименьшим значением на этом отрезке.

График функции y =f(x) называется выпуклым на интервале (a; b) , если он расположен ниже любой своей касательной на этом интервале.

График функции y =f(x) называется вогнутым на интервале (a; b) , если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c) .

Примеры.

Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.

Теорема . Пусть y =f(x) дифференцируема на (a; b) . Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ""(x ) < 0, то график функции на этом интервале выпуклый, если же f ""(x ) > 0 – вогнутый.

Доказательство . Предположим для определенности, что f ""(x ) < 0 и докажем, что график функции будет выпуклым.

Возьмем на графике функции y = f(x) произвольную точку M 0 с абсциссой x 0 Î (a ; b ) и проведем через точку M 0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.

Итак, уравнение кривой имеет вид y = f(x) . Обозначим ординату касательной, соответствующую абсциссе x . Тогда . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет .

Разность f(x) – f(x 0) преобразуем по теореме Лагранжа , где c между x и x 0 .

Таким образом,

К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: , где c 1 между c 0 и x 0 . По условию теоремы f ""(x ) < 0. Определим знак произведения второго и третьего сомножителей.

Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x 0 Î (a ; b ), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.

Примеры .

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба .

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема . Пусть кривая определяется уравнением y = f(x) . Если f ""(x 0) = 0 или f ""(x 0) не существует и при переходе через значение x = x 0 производная f ""(x ) меняет знак, то точка графика функции с абсциссой x = x 0 есть точка перегиба.

Доказательство . Пусть f ""(x ) < 0 при x < x 0 и f ""(x ) > 0 при x > x 0 . Тогда при x < x 0 кривая выпукла, а при x > x 0 – вогнута. Следовательно, точка A , лежащая на кривой, с абсциссой x 0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ""(x ) > 0 при x < x 0 и f ""(x ) < 0 при x > x 0 .

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.

АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.

Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.

Прямая называется асимптотой графика функции y = f(x) , если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.

Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.

Будем в дальнейшем различать асимптоты вертикальные и наклонные.

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

Пусть при x → x 0 с какой-либо стороны функция y = f(x) неограниченно возрастает по абсолютной величине, т.е. или или . Тогда из определения асимптоты следует, что прямая x = x 0 является асимптотой. Очевидно и обратное, если прямая x = x 0 является асимптотой, т. о. .

Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x → x 0 – 0 или x → x 0 + 0, x = x 0

Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x 0 , при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x 0 .

Примеры.

НАКЛОННЫЕ АСИМПТОТЫ

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b . Наша задача найти коэффициенты k и b .

Теорема . Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда . Аналогичное утверждение верно и при x → –∞.

Доказательство . Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к оси Ox . Тогда из ΔMNP следует, что . Так как φ постоянный угол (φ ≠ π/2), то , но

Для определения выпуклости (вогнутости) функции на некотором интервале можно использовать следующие теоремы.

Теорема 1. Пусть функция определена и непрерывна на интервале и имеет конечную производную . Для того, чтобы функция была выпуклой (вогнутой) в , необходимо и достаточно, чтобы ее производная убывала (возрастала) на этом интервале.

Теорема 2. Пусть функция определена и непрерывна вместе со своей производной на и имеет внутри непрерывную вторую производную . Для выпуклости (вогнутости) функции в необходимо и достаточно, чтобы внутри

Докажем теорему 2 для случая выпуклости функции .

Необходимость. Возьмем произвольную точку . Разложим функцию около точки в ряд Тейлора

Уравнение касательной к кривой в точке, имеющей абсциссу :

Тогда превышение кривой над касательной к ней в точке равно

Таким образом, остаток равен величине превышения кривой над касательной к ней в точке . В силу непрерывности , если , то и для , принадлежащих достаточно малой окрестности точки , а потому, очевидно, и для любого отличного от значения , принадлежащего к указанной окрестности.

Значит, график функции лежит выше касательной и кривая выпукла в произвольной точке .

Достаточность. Пусть кривая выпукла на промежутке . Возьмем произвольную точку .

Аналогично предыдущему разложим функцию около точки в ряд Тейлора

Превышение кривой над касательной к ней в точке, имеющей абсциссу , определяемой выражением равно

Так как превышение положительно для достаточно малой окрестности точки , то положительна и вторая производная . При стремлении получаем, что для произвольной точки .

Пример. Исследовать на выпуклость (вогнутость) функцию .

Ее производная возрастает на всей числовой оси, значит по теореме 1 функция вогнута на .

Ее вторая производная , поэтому по теореме 2 функция вогнута на .

3.4.2.2 Точки перегиба

Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.

Из этого определения следует, что точки перегиба - это точки точки экстремума первой производной. Отсюда вытекают следующие утверждения для необходимого и достаточного условий перегиба.

Теорема (необходимое условие перегиба) . Для того чтобы точка являлась точкой перегиба дважды дифференцируемой функции , необходимо, чтобы ее вторая производная в этой точке равнялась нулю () или не существовала.

Теорема (достаточное условие перегиба). Если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то есть точка перегиба.

Отметим, что в самой точке вторая производная может не существовать.

Геометрическая интерпретация точек перегиба иллюстрируется рис. 3.9

В окрестности точки функция выпукла и график ее лежит ниже касательной, проведенной в этой точке. В окрестности точки функция вогнута и график ее лежит выше касательной, проведенной в этой точке. В точке перегиба касательная разделяет график функции на области выпуклости и вогнутости.

3.4.2.3 Исследование функции на выпуклость и наличие точек перегиба

1. Найти вторую производную .

2. Найти точки, в которых вторая производная или не существует.

Рис. 3.9.

3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости или вогнутости и наличии точек перегиба.

Пример. Исследовать функцию на выпуклость и наличие точек перегиба.

2. Вторая производная равна нулю при .

3. Вторая производная меняет знак при , значит точка - точка перегиба.

На интервале , значит функция выпукла на этом интервале.

На интервале , значит функция вогнута на этом интервале.

3.4.2.4 Общая схема исследования функций и построения графика

При исследовании функции и построении ее графика рекомендуется использовать следующую схему:

Найти область определения функции.
Исследовать функцию на четность - нечетность. Напомним, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Найти вертикальные асимптоты.
Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
Найти экстремумы и интервалы монотонности функции.
Найти интервалы выпуклости функции и точки перегиба.
Найти точки пересечения с осями координат.

Исследование функции проводится одновременно с построением ее графика.

Пример. Исследовать функцию и построить ее график.

1. Область определения функции - .

2. Исследуемая функция - четная , поэтому ее график симметричен относительно оси ординат.

3. Знаменатель функции обращается в ноль при , поэтому график функции имеет вертикальные асимптоты и .

Точки являются точками разрыва второго рода, так как пределы слева и справа в этих точках стремятся к .

4. Поведение функции в бесконечности.

Поэтому график функции имеет горизонтальную асимптоту .

5. Экстремумы и интервалы монотонности. Находим первую производную

При , поэтому в этих интервалах функция убывает.

При , поэтому в этих интервалах функция возрастает.

При , поэтому точка является критической точкой.

Находим вторую производную

Так как , то точка является точкой минимума функции .

6. Интервалы выпуклости и точки перегиба.

Функция при , значит на этом интервале функция вогнута.

Функция при , значит на этих интервалах функция выпукла.

Функция нигде не обращается в ноль, значит точек перегиба нет.

7. Точки пересечения с осями координат.

Уравнение , имеет решение , значит точка пересечения графика функции с осью ординат (0, 1).

Уравнение не имеет решения, значит точек пересечения с осью абсцисс нет.

С учетом проведенного исследования можно строить график функции

Схематически график функции изображен на рис. 3.10 .

Рис. 3.10.

3.4.2.5 Асимптоты графика функции

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки () до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.

Общая схема исследования функции и построение графика.
1. Исследование функции на выпуклость и вогнутость.

Асимптоты графика функции.

Введение.

В школьном курсе математики вы уже встречались с необходимостью построения графиков функций. В , вы использовали способ построения по точкам. Следует отметить, что он прост по идее и сравнительно быстро приводит к цели. В случаях, когда функция непрерывна и изменяется довольно плавно, такой способ может обеспечить и необходимую степень точности графического представления. Для этого нужно брать побольше точек, чтобы достичь определённой густоты их размещения.

Предположим теперь, что функция в отдельных местах имеет особенности в своём «поведении»: либо её значения где-то на малом участке резко меняются, либо имеют место разрывы. Наиболее существенные части графика таким способом могут и не быть обнаружены.

Это обстоятельство и снижает ценность способа построения графика «по точкам».

Существует второй способ построения графиков, основанный на аналитическом исследовании функций. Он выгодно отличается от способа, рассмотренного в школьном курсе математики.

1. Исследование функции на выпуклость и вогнутость .

Пусть функция
дифференцируема на интервале (а, в). Тогда существует касательная к графику функции в любой точке
этого графика (
), причем касательная не параллельна оси OY , так как ее угловой коэффициент, равный
, конечен.

О
пределение Будем говорить, что график функции
на (а, в) имеет выпускать, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а, в).

а) вогнутая кривая б) выпуклая кривая

Теорема 1 (необходимое условие выпуклости (вогнутости) кривой).

Если график дважды дифференцируемой функции выпуклая (вогнутая) кривая , то вторая производная на интервале (а, в) отрицательна (положительна) на этом интервале.

Теорема 2 (достаточное условие выпуклости (вогнутости) кривой).

Если функция дважды дифференцируема на (а, в) и
(
) во всех точках этого интервала, то кривая, являющаяся графиком функции выпуклая (вогнутая) на этом интервале.

Точки перегиба графика функции.

Определение Точка
называется точкой перегиба графика функции , если в точке
график имеет касательную, и существует такая окрестность точки , в пределах которой график функции слева и справа точки имеет разные направления выпуклости.

Очевидно, что в точке перегиба касательная пересекает график функции, так как с одной стороны от этой точки график лежит над касательной, а с другой – под нею, т. е. в окрестности точки перегиба график функции геометрически переходит с одной стороны касательной на другую и «перегибается» через нее. Отсюда и произошло название «точки перегиба».

Теорема 3 (необходимое условие точки перегиба). Пусть график функции имеет перегиб в точке и пусть функция имеет в точке

непрерывную вторую производную. Тогда

.
Не всякая точка , для которой , является точкой перегиба. Например, график функции

не имеет перегиба в точке (0, 0), хотя

при

. Поэтому равенство нулю второй производной является лишь необходимым условием перегиба.

Точки графика, для которых называется критическими точками II -го рода. Необходимо дополнительно исследовать вопрос о наличии перегибав каждой критической точке.

Теорема 4 (достаточное условие точки перегиба). Пусть функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах указанной окрестности
имеет разные знаки слева и справа от точки , то график имеет перегиб в точке .
Замечание. Теорема остается верной, если
имеет вторую производную в некоторой окрестности точки , за исключением самой точки , и существует касательная к графику функции в точке
. Тогда, если в пределах указанной окрестности имеет разные знаки слева и справа от точки , то график к функции имеет перегиб в точке .
Схема исследования функции на выпуклость, вогнутость, точки перегиба.

Пример. Исследовать функцию
на выпуклость, вогнутость, точки перегиба.
1.

2.
,
=

3. не существует при

)	1	(1, +)
-		+
	1

Асимптоты графика функции.

При исследовании поведения функции при
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют.

Определение 1. Прямая

называется асимптотой кривой L, если расстояние от точки кривой до этой прямой стремится к нулю при удалении точки по кривой к бесконечности. Существует три вида асимптот: вертикальные, горизонтальные, наклонные.

Определение 2. Прямая
называется вертикальной асимптотой графика функции , если хотя бы один из односторонних пределов равен
, т. е. или

Например, график функции
имеет вертикальную асимптоту
, т. к.
, а
.

Определение 3. Прямая у=А называется горизонтальной асимптотой графика функции при

если

Например, график функции имеет горизонтальную асимптоту у=0 , т. к.
.

Определение 4. Прямая

(

) называется наклонной асимптотой графика функции при

если

;

Если хотя бы один из пределов не существует, то кривая асимптот не имеет. Если, то следует искать эти пределы отдельно, при и
.

Например. Найти асимптоты графика функции

; х=0 – вертикальная асимптота

;
.

- наклонная асимптота.
4. Схема полного исследования функции и построение графика.

Рассмотрим примерную схему по которой целесообразно исследовать поведение функции и строить ее график.

Пример. Исследовать функцию

и построить ее график.

1. , кроме х=-1.

2.
функция ни четная ни нечетная

-

-

+

+

y

-4

т р.

0

Заключение.
Важной особенностью рассмотренного способа является то, что в его основе лежит прежде всего обнаружение и изучение характерных особенностей в поведении кривой. Места, где функция изменяется плавно, не изучаются особенно подробно, да и нет надобности в таком изучении. Зато те места , где функция имеет какие-либо особенности в поведении, подлежат полному исследованию и максимально точному графическому изображению. Этими особенностями являются точки максимума, минимума, точки разрыва функции и др.

Определение направления вогнутости и перегибов, а также указанный способ нахождения асимптот дают возможность провести исследование функций ещё более детально и получить более точное представление об их графиках.

Инструкция

Точки перегиба функции должны принадлежать области ее определения, которую нужно найти в первую очередь. График функции – это линия, которая может быть непрерывной или иметь разрывы, монотонно убывать или возрастать, иметь минимальные или максимальные точки (асимптоты), быть выпуклой или вогнутой. Резкая смена двух последних состояний и называется перегибом.

Необходимое условие существования перегиба функции состоит в равенстве второй нулю. Таким образом, дважды продифференцировав функцию и приравняв получившееся выражение нулю, можно найти абсциссы возможных точек перегиба.

Это условие следует из определения свойств выпуклости и вогнутости графика функции, т.е. отрицательному и положительному значению второй производной. В точке перегиба резкая смена этих свойств, значит, производная переходит нулевую отметку. Однако равенства нулю еще недостаточно для того, чтобы обозначить перегиб.

Существует два достаточных того, что найденная на предыдущем этапе абсцисса принадлежит точке перегиба:Через эту точку можно провести касательную к функции. Вторая производная имеет разные знаки справа и слева от предполагаемой точки перегиба. Таким образом, ее существование в самой точке необязательно, достаточно определить, что в ней она меняет знак.Вторая производная функции равна нулю, а третья – нет.

Первое достаточное условие является универсальным и применяется чаще других. Рассмотрим иллюстрирующий пример: у = (3 х + 3) ∛(х - 5).

Решение.Найдите область определения. В данном случае ограничений нет, следовательно, ею является все пространство действительных чисел. Вычислите первую производную:у’ = 3 ∛(х - 5) + (3 х + 3)/∛(х - 5)².

Обратите внимание на появление дроби. Из него следует, что область определения производной ограничена. Точка х = 5 является выколотой, а значит, через нее может проходить касательная, что отчасти соответствует первому признаку достаточности перегиба.

Определите односторонние пределы для получившегося выражения при х → 5 – 0 и х → 5 + 0. Они равны -∞ и +∞. Вы доказали, что через точку х=5 проходит вертикальная касательная. Эта точка может оказаться точкой перегиба, но сначала вычислите вторую производную:У’’ = 1/∛(х - 5)² + 3/∛(х - 5)² – 2/3 (3 х + 3)/∛(х - 5)^5 = (2 х – 22)/∛(х - 5)^5.

Опустите знаменатель, поскольку точку х = 5 вы уже учли. Решите уравнение 2 х – 22 = 0. Оно имеет единственный корень х = 11.Последний этап – подтверждение того, что точки х = 5 и х = 11 являются точками перегиба. Проанализируйте поведение второй производной в их окрестностях. Очевидно, что в точке х = 5 она меняет знак с «+» на «-», а в точке х = 11 – наоборот. Вывод: обе точки являются точками перегиба. Выполнено первое достаточное условие.