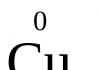Racionalizačná metóda vám umožňuje prejsť z nerovnosti obsahujúcej komplexné exponenciálne, logaritmické atď. výrazov, na ekvivalentnú jednoduchšiu racionálnu nerovnosť.

Preto skôr, ako začneme hovoriť o racionalizácii v nerovnostiach, povedzme si o ekvivalencii.

rovnocennosť

Ekvivalent alebo ekvivalent nazývané rovnice (nerovnice), ktorých množiny koreňov sa zhodujú. Rovnice (nerovnice), ktoré nemajú korene, sa tiež považujú za ekvivalentné.

Príklad 1 Rovnice a sú ekvivalentné, pretože majú rovnaké korene.

Príklad 2 Rovnice a sú tiež ekvivalentné, pretože riešením každej z nich je prázdna množina.

Príklad 3 Nerovnice a sú ekvivalentné, pretože riešením oboch je množina .

Príklad 4 a sú nerovné. Riešenie druhej rovnice je iba 4 a riešenie prvej rovnice je 4 aj 2.

Príklad 5 Nerovnosť je ekvivalentná nerovnici, pretože v oboch nerovnostiach je riešenie 6.

To znamená, že ekvivalentné nerovnosti (rovnice) môžu mať od podobnosti veľmi ďaleko.

V skutočnosti, keď takto riešime zložité, dlhé rovnice (nerovnice) a dostaneme odpoveď, nemáme v rukách nič iné ako rovnicu (nerovnosť) ekvivalentnú tej pôvodnej. Vzhľad je iný, ale podstata je rovnaká!

Príklad 6 Pripomeňme si, ako sme riešili nerovnosť pred oboznámením sa s metódou intervalov. Pôvodnú nerovnosť sme nahradili súborom dvoch systémov:

To znamená, že nerovnosť a posledná množina sú navzájom ekvivalentné.

Tiež by sme mohli mať v rukách zbierku

nahraďte ju nerovnosťou , ktorú je možné v okamihu vyriešiť intervalovou metódou.

Priblížili sme sa k metóde racionalizácie v logaritmických nerovnostiach.

Racionalizačná metóda v logaritmických nerovnostiach

Zoberme si nerovnosť.

Reprezentujeme 4 ako logaritmus:

Máme do činenia s premenlivým základom logaritmu, preto v závislosti od toho, či je základ logaritmu väčší ako 1 alebo menší ako 1 (čiže máme do činenia s rastúcou alebo klesajúcou funkciou), znamienko nerovnosti zostane, resp. zmeniť na "". Preto existuje kombinácia (kombinácia) dvoch systémov:

Ale, POZOR, tento systém treba riešiť s prihliadnutím na ODZ! Zámerne som nenačítal systém ODZ, aby sa nestratila hlavná myšlienka.

Pozrite, teraz prepíšeme náš systém takto (presunieme všetko v každom riadku nerovnosti na ľavú stranu):

Nepripomína vám to nič? Analogicky s príklad 6 túto množinu systémov nahradíme nerovnosťou:

Po vyriešení tejto nerovnosti na ODZ dostaneme riešenie nerovnosti .

Najprv nájdime ODZ pôvodnej nerovnosti:

Teraz sa poďme rozhodnúť

Riešenie poslednej nerovnosti s prihliadnutím na ODZ:

Takže tu je táto „magická“ tabuľka:

Upozorňujeme, že tabuľka funguje za podmienok

kde sú funkcie,

- funkcia alebo číslo,

- jedna z postáv

Všimnite si tiež, že druhý a tretí riadok tabuľky sú dôsledkom prvého. V druhom riadku je 1 znázornená predtým ako a v treťom riadku je 0 znázornená ako .

A pár ďalších užitočných dôsledkov (dúfam, že ľahko pochopíte, odkiaľ pochádzajú):

kde sú funkcie,

- funkcia alebo číslo,

- jedna z postáv

Racionalizačná metóda v exponenciálnych nerovnostiach

Vyriešme nerovnosť.

Riešenie pôvodnej nerovnosti je ekvivalentné s riešením nerovnosti

Odpoveď: .

Tabuľka pre racionalizáciu v exponenciálnych nerovnostiach:

– funkcie , – funkcia alebo číslo, – jeden zo znakov Tabuľka funguje pod podmienkou . Aj v treťom, štvrtom riadku - dodatočne -

Opäť si v skutočnosti musíte zapamätať prvý a tretí riadok tabuľky. Druhý riadok je špeciálny prípad prvého a štvrtý riadok je špeciálny prípad tretieho.

Racionalizačná metóda v nerovnostiach obsahujúcich modul

Pri práci s nerovnicami typu , kde sú funkcie nejakej premennej, sa môžeme riadiť nasledujúcimi ekvivalentnými prechodmi:

Poďme vyriešiť nerovnosť “.

A Tu ponúknuť viac zvážte niekoľko príkladov na tému „Racionalizácia nerovností“.

Sekcie: Matematika

Pri riešení logaritmických nerovností sa často vyskytujú problémy s premenlivou základňou logaritmu. Takže nerovnosť formy

je štandardná školská nerovnosť. Na jeho vyriešenie sa spravidla používa prechod na ekvivalentnú sadu systémov:

Nevýhodou tejto metódy je nutnosť riešiť sedem nerovností, nerátajúc dva systémy a jednu množinu. Aj pri daných kvadratických funkciách môže populačné riešenie vyžadovať veľa času.

Je možné navrhnúť alternatívny, časovo menej náročný spôsob riešenia tejto štandardnej nerovnosti. Aby sme to dosiahli, berieme do úvahy nasledujúcu vetu.

Veta 1. Nech je spojitá rastúca funkcia na množine X. Potom na tejto množine bude znamienko prírastku funkcie zhodné so znamienkom prírastku argumentu, t.j. , Kde .

Poznámka: ak na množine X funguje nepretržité znižovanie, potom .

Vráťme sa k nerovnosti. Prejdime k desiatkovému logaritmu (môžete prejsť na ktorýkoľvek s konštantným základom väčším ako jedna).

Teraz môžeme použiť teorém a všimnúť si v čitateli prírastok funkcií a v menovateli. Takže je to pravda

V dôsledku toho sa počet výpočtov vedúcich k odpovedi zníži približne na polovicu, čo šetrí nielen čas, ale tiež umožňuje potenciálne robiť menej aritmetických a neopatrných chýb.

Príklad 1

Porovnaním s (1) zistíme , , .

Prechodom do (2) budeme mať:

Príklad 2

Porovnaním s (1) nájdeme , , .

Prechodom do (2) budeme mať:

Príklad 3

Keďže ľavá strana nerovnosti je rastúca funkcia pre a , potom je odpoveď nastavená .

Súbor príkladov, v ktorých možno použiť termín 1, možno ľahko rozšíriť, ak sa vezme do úvahy termín 2.

Pustite na scénu X funkcie , , , sú definované a na tejto množine sa znamienka a zhodujú, t.j. potom to bude spravodlivé.

Príklad 4

Príklad 5

Pri štandardnom prístupe je príklad riešený podľa schémy: súčin je menší ako nula, keď faktory majú rôzne znamienka. Tie. uvažujeme o množine dvoch systémov nerovností, v ktorých, ako bolo naznačené na začiatku, sa každá nerovnosť rozpadá na ďalších sedem.

Ak vezmeme do úvahy vetu 2, potom každý z faktorov, berúc do úvahy (2), môže byť nahradený inou funkciou, ktorá má rovnaké znamienko v tomto príklade O.D.Z.

Metóda nahradenia prírastku funkcie prírastkom argumentu, berúc do úvahy vetu 2, sa ukazuje ako veľmi výhodná pri riešení typických problémov C3 USE.

Príklad 6

Príklad 7

. Označme . Získajte

. Všimnite si, že nahradenie znamená: . Keď sa vrátime k rovnici, dostaneme .

Príklad 8

Vo vetách, ktoré používame, neexistujú žiadne obmedzenia na triedy funkcií. V tomto článku boli ako príklad aplikované vety na riešenie logaritmických nerovností. Nasledujúcich niekoľko príkladov demonštruje prísľub metódy na riešenie iných typov nerovností.

Mestská autonómna vzdelávacia inštitúcia "Yarkovskaja stredná škola"

Vzdelávací projekt

Riešenie logaritmických nerovností racionalizačnou metódou

MAOU "Yarkovskaya stredná škola"

Shanskikh Daria

Vedúci: učiteľ matematiky

MAOU "Yarkovskaya stredná škola"

Jarkovo 2013

1) Úvod……………………………………………………………………….2

2) Hlavná časť………………………………………………..3

3) Záver…………………………………………………………..9

4) Zoznam použitej literatúry 10

5) Žiadosti………………………………………………………………… 11-12

1. Úvod

Pri riešení úloh USE z časti „C“ a najmä v úlohách C3 sa často vyskytujú nerovnosti obsahujúce logaritmické výrazy s neznámou základňou logaritmu. Tu je príklad štandardnej nerovnosti:

Na riešenie takýchto úloh sa spravidla používa klasická metóda, to znamená prechod na ekvivalentný súbor systémov.

Pri štandardnom prístupe je príklad riešený podľa schémy: súčin je menší ako nula, keď faktory majú rôzne znamienka. To znamená, že sa uvažuje o súbore dvoch systémov nerovností, v ktorých sa každá nerovnosť rozpadne na ďalších sedem. Preto je možné navrhnúť menej časovo náročný spôsob riešenia tejto štandardnej nerovnosti. Ide o racionalizačnú metódu, ktorá je v matematickej literatúre známa ako dekompozícia.

Pri realizácii projektu som si stanovil tieto ciele: :

1) Zvládnite túto rozhodovaciu techniku

2) Precvičiť si zručnosti riešenia úloh C3 z tréningovej a diagnostickej práce v roku 2013.

Cieľ projektuje náuka o teoretickom zdôvodnení metódy racionalizácie.

Relevantnosťpráca spočíva v tom, že táto metóda umožňuje úspešne riešiť logaritmické nerovnosti časti C3 Jednotnej štátnej skúšky z matematiky.

2. Hlavná časť

Zvážte logaritmickú nerovnosť formulára

veľkosť písma:14,0pt; line-height:150%">, (1)

kde font-size:14.0pt;line-height:150%"> Štandardná metóda na riešenie takejto nerovnosti zahŕňa analýzu dvoch prípadov do oblastí s prijateľnými hodnotami nerovnosti.

V prvom prípade keď základy logaritmov spĺňajú podmienku

veľkosť písma:14,0pt; line-height:150%">, znamienko nerovnosti je obrátené: font-size:14.0pt;line-height:150%"> V druhom prípade keď základ spĺňa podmienku, znak nerovnosti je zachovaný: .

Na prvý pohľad je všetko logické, zvážme dva prípady a potom spojme odpovede. Pravda, pri zvažovaní druhého prípadu vzniká istý diskomfort – na 90 percent musíte zopakovať výpočty z prvého prípadu (transformovať, nájsť korene pomocných rovníc, určiť intervaly monotónnosti znamienka). Vynára sa prirodzená otázka – dá sa to všetko nejako skĺbiť?

Odpoveď na túto otázku je obsiahnutá v nasledujúcej vete.

Veta 1. logaritmická nerovnosť

font-size:14.0pt;line-height:150%">je ekvivalentný nasledujúcemu systému nerovností :

veľkosť písma:14,0pt; line-height:150%"> (2)

Dôkaz.

1. Začnime tým, že prvé štyri nerovnosti systému (2) definujú množinu prípustných hodnôt pôvodnej logaritmickej nerovnosti. Obráťme teraz svoju pozornosť na piatu nerovnosť. Ak veľkosť písma:14,0pt; line-height:150%">, potom bude prvý faktor tejto nerovnosti záporný. Pri zmenšení o ňu budete musieť zmeniť znamienko nerovnosti na opačné, potom dostanete nerovnosť .

Ak , To prvý faktor piatej nerovnosti je pozitívny, znížime ho bez zmeny znamienka nerovnosti, dostaneme nerovnosť font-size:14.0pt;line-height: 150%">. Piata nerovnosť systému teda zahŕňa oba prípady predchádzajúcej metódy.

Termín je osvedčený.

Hlavné ustanovenia teórie racionalizačnej metódy.

Racionalizačná metóda spočíva v nahradení komplexného výrazu F(x ) k jednoduchšiemu výrazu G(x ), pod ktorým je nerovnosť G(x )SK" style="font-size:14.0pt;line-height:150%;font-family:Calibri">F(X )0 v doméne expresie F(x).

Vyberme si niektoré výrazy F a ich zodpovedajúce racionalizačné výrazy G , kde u , v , , p , q - výrazy s dvoma premennými ( u > 0; u ≠ 1; v > 0, > 0), a - pevné číslo (a > 0, a ≠ 1).

Dôkaz

1. Nechajte logav - logaφ > 0, to jest logav > logaφ, a a > 0, a ≠ 1, v > 0,

φ > 0.

Ak 0< a < 1, то по свойству убывающей логарифмической функции имеем v < φ . Preto platí systém nerovností

a -1<0

v – φ < 0

Odkiaľ nasleduje nerovnosť (a – 1)( v – φ ) > 0 true na doméne výrazuF = logav - logaφ.

Ak a > 1, To v > φ . Preto máme nerovnosť ( a – 1)( v – φ )> 0. Naopak, ak nerovnosť ( a – 1)( v – φ )> 0 v rozsahu prijateľných hodnôt ( a > 0, a ≠ 1, v> 0, φ > 0),potom na tejto doméne je ekvivalentná kombinácii dvoch systémov.

a – 1<0 a – 1 > 0

v – φ < 0 v – φ > 0

Každý systém znamená nerovnosťlogav > logaφ, to jest logav - logaφ > 0.

Podobne uvažujeme o nerovnostiach F< 0, F ≤ 0, F ≥ 0.

2. Nechajte nejaké číslo A> 0 a A≠ 1, potom máme

logo v- loguφ = EN-US" style="font-size:14.0pt;line-height:150%">v - 1)( u- 1) (φ -u).

4. Z nerovnosti UV- uφ > 0 by mal UV > uφ. Nech je teda číslo a > 1loga UV > logauφ alebo

( u – φ) loga u > 0.

Preto, berúc do úvahy zmenu 1b a podmienkua > 1 dostaneme

( v – φ)( a – 1)( u – 1) > 0, ( v – φ)( u – 1) > 0. Podobne dokazujeme nerovnosti F< 0,

F ≤ 0, F ≥ 0.

5. Dôkaz je podobný dôkazu 4.

6. Dôkaz substitúcie 6 vyplýva z ekvivalencie nerovností | p | > | q | a p2 > q2

(|p|< | q | и p 2 < q 2 ).

Porovnajme objem riešenia nerovníc obsahujúcich premennú na báze logaritmu klasickou metódou a racionalizačnou metódou

3. Záver

Verím, že úlohy, ktoré som si pri výkone práce stanovil, sa mi podarilo splniť. Projekt má praktický význam, keďže metóda navrhovaná v práci umožňuje výrazne zjednodušiť riešenie logaritmických nerovností. V dôsledku toho sa počet výpočtov vedúcich k odpovedi zníži približne na polovicu, čo šetrí nielen čas, ale tiež umožňuje potenciálne robiť menej aritmetických a neopatrných chýb. Teraz pri riešení problémov C3 používam túto metódu.

4. Zoznam použitej literatúry

1. , – Metódy riešenia nerovníc s jednou premennou. – 2011.

2. - Sprievodca matematikou. - 1972.

3. - Matematika pre žiadateľa. Moskva: MTSNMO, 2008.

Ežová Elena Sergejevna
Názov práce: učiteľ matematiky
Vzdelávacia inštitúcia: MOU "Škola №77"
lokalita: Saratov
Názov materiálu: metodický vývoj
Predmet: Racionalizačná metóda pri riešení nerovností v príprave na skúšku "
Dátum publikácie: 16.05.2018
kapitola:úplné vzdelanie

Je zrejmé, že rovnakú nerovnosť možno vyriešiť niekoľkými spôsobmi. Našťastie

zvoleným spôsobom alebo, ako sme zvykli hovorievať, racionálnym spôsobom, ľubovoľným

nerovnosť sa vyrieši rýchlo a jednoducho, jej riešenie bude krásne a zaujímavé.

Chcel by som podrobnejšie zvážiť takzvanú racionalizačnú metódu, keď

riešenie logaritmických a exponenciálnych nerovností, ako aj nerovností obsahujúcich

premenná pod znakom modulu.

Hlavná myšlienka metódy.

Metóda meniacich sa faktorov sa používa na riešenie nerovností zredukovaných do tvaru

Kde je symbol

» označuje jedno zo štyroch možných znakov nerovnosti:

Pri riešení nerovnosti (1) nás v čitateli zaujíma len znamienko ľubovoľného činiteľa

alebo menovateľ, a nie jeho absolútnu hodnotu. Preto, ak z nejakého dôvodu sme

s touto násobilkou je nepohodlné pracovať, môžeme ju nahradiť inou

sa zhoduje s ním v regióne definície nerovnosti a má v tomto regióne

rovnaké korene.

To určuje hlavnú myšlienku metódy nahradenia multiplikátora. Je dôležité to napraviť

skutočnosť, že nahradenie faktorov sa vykonáva len za podmienky, že sa nerovnosť zníži

do formulára (1), teda vtedy, keď je potrebné porovnávať súčin s nulou.

Hlavná časť nahradenia je spôsobená nasledujúcimi dvoma ekvivalentnými vyhláseniami.

Výrok 1. Funkcia f(x) je striktne rastúca práve vtedy, ak pre

akékoľvek hodnoty t

) sa zhoduje s

znamienko s rozdielom (f(t

)), teda f<=>(t

(↔ znamená zhodu znamienka)

Výrok 2. Funkcia f(x) je striktne klesajúca práve vtedy, ak pre

akékoľvek hodnoty t

z oblasti funkčného rozdielu (t

) sa zhoduje s

znamienko s rozdielom (f(t

)), teda f ↓<=>(t

Opodstatnenosť týchto tvrdení vyplýva priamo z definície striktne

monotónna funkcia. Podľa týchto vyjadrení možno konštatovať, že

Rozdiel stupňov v rovnakom základe sa vždy zhoduje v znamienku s

súčin rozdielu medzi ukazovateľmi týchto stupňov a odchýlky základne od jednoty,

Rozdiel logaritmov v rovnakom základe sa vždy zhoduje v znamienku s

potom súčin rozdielu medzi číslami týchto logaritmov a odchýlkou ​​základne od jednoty

Skutočnosť, že rozdiel nezáporných veličín má rovnaké znamienko ako rozdiel

štvorcov týchto hodnôt, umožňuje nasledujúce substitúcie:

Vyriešte nerovnosť

Riešenie.

Prejdime k ekvivalentnému systému:

Z prvej nerovnosti dostaneme

Druhá nerovnosť platí pre všetkých

Z tretej nerovnosti dostaneme

Takže množina riešení pôvodnej nerovnosti:

Vyriešte nerovnosť

Riešenie.

Poďme vyriešiť nerovnosť:

Odpoveď: (−4; −3)

Vyriešte nerovnosť

Prinesme nerovnosť do formy, v ktorej je rozdiel medzi hodnotami logaritmu

Nahradme rozdiel v hodnotách logaritmickej funkcie rozdielom v hodnotách argumentu. IN

čitateľ je rastúca funkcia a menovateľ je klesajúci, takže znamienko nerovnosti

sa zmení na opak. Je dôležité nezabudnúť vziať do úvahy rozsah

logaritmická funkcia, takže táto nerovnosť je ekvivalentná systému nerovností.

Korene čitateľa: 8; 8;

Koreň menovateľa: 1

Vyriešte nerovnosť

Nahradme v čitateli rozdiel medzi modulmi dvoch funkcií rozdielom medzi ich druhými mocninami a v

menovateľ je rozdiel medzi hodnotami logaritmickej funkcie a rozdiel medzi argumentmi.

V menovateli je funkcia klesajúca, čo znamená, že znamienko nerovnosti sa zmení na

opak.

V tomto prípade je potrebné vziať do úvahy doménu definície logaritmiky

Prvú nerovnosť riešime intervalovou metódou.

Korene čitateľa:

Korene menovateľa:

Vyriešte nerovnosť

Nahradme v čitateli a menovateli rozdiel medzi hodnotami monotónnych funkcií rozdielom

hodnoty argumentov, berúc do úvahy oblasť definície funkcií a povahu monotónnosti.

Korene čitateľa:

Korene menovateľa:

Najčastejšie používané substitúcie (okrem O D 3).

a) Zmena násobiteľov znamienkovej konštanty.

b) Nahradenie nekonštantných faktorov modulom.

c) Nahradenie nekonštantných faktorov exponenciálnymi a logaritmickými

výrazov.

Riešenie. ODZ:

Výmena multiplikátorov:

Máme systém:

V tejto nerovnosti sú faktory

považovať za rozdiely nezáporných hodnôt, pretože výrazy 1

ODZ môže nadobúdať kladné aj záporné hodnoty.

Máme systém:

Výmena multiplikátorov:

Máme systém:

Výmena multiplikátorov:

Máme systém:

Výmena multiplikátorov:

Máme systém:

V dôsledku toho máme: x

racionalizačná metóda(metóda rozkladu, metóda náhrady multiplikátora, náhradná metóda

funkcie, znakové pravidlo) spočíva v nahradení komplexného výrazu F(x) výrazom viac

jednoduchý výraz G(x), pre ktorý platí nerovnosť G(x)

0 je ekvivalentná nerovnosti F (x

0 v doméne výrazu F(x).

Sekcie: Matematika

Prax kontroly skúšok ukazuje, že najväčším problémom pre školákov je riešenie transcendentálnych nerovností, najmä logaritmických nerovností s premenlivým základom. Zhrnutie lekcie, ktoré je vám predložené, je preto prezentáciou metódy racionalizácie (iné názvy sú metóda rozkladu (Modenov V.P.), metóda nahradenia faktorov (Golubev V.I.)), ktorá vám umožňuje znížiť zložité logaritmické, exponenciálne, kombinované nerovností na systém jednoduchších racionálnych nerovností. Metóda intervalov aplikovaná na racionálne nerovnice v čase, keď sa študovala téma „Riešenie logaritmických nerovníc“, bola spravidla dobre zvládnutá a rozpracovaná. Študenti preto s veľkým záujmom a nadšením vnímajú tie metódy, ktoré im umožňujú riešenie zjednodušiť, skrátiť a v konečnom dôsledku ušetriť čas na skúške na riešenie iných úloh.

Ciele lekcie:

• vzdelávacie: aktualizácia základných poznatkov pri riešení logaritmických nerovníc; zavedenie nového spôsobu riešenia nerovností; zlepšenie rozhodovacích schopností
• Vzdelávacie: rozvoj matematických obzorov, matematická reč, analytické myslenie
• Vzdelávacie: výchova k presnosti a sebaovládaniu.

POČAS VYUČOVANIA

1. Organizačný moment. pozdravujem. Stanovenie cieľov lekcie.

2. Prípravná fáza:

Vyriešte nerovnosti:

3. Kontrola domácich úloh(č. 11.81*a)

Pri riešení nerovnosti

Na riešenie logaritmických nerovností s variabilnou základňou ste museli použiť nasledujúcu schému:

Tie. Je potrebné zvážiť 2 prípady: základňa je väčšia ako 1 alebo základňa je menšia ako 1.

4. Vysvetlenie nového materiálu

Ak sa na tieto vzorce pozorne pozriete, všimnete si, že je to znak rozdielu g(X) – h(X) sa zhoduje so znamienkom rozdielu log f(X) g(X) - denník f(X) h(X) v prípade zvyšujúcej sa funkcie ( f(X) > 1, t.j. f(X) – 1 > 0) a je opačný ako znamienko logaritmu rozdielu f(X) g(X) - denník f(X) h(X) v prípade klesajúcej funkcie (0< f(X) < 1, т.е. f(X) – 1 < 0)

Preto je možné túto množinu zredukovať na systém racionálnych nerovností:

To je podstata racionalizačnej metódy – nahradiť zložitejší výraz A jednoduchším výrazom B, ktorý je racionálny. V tomto prípade bude nerovnosť В V 0 ekvivalentná nerovnosti А V 0 na definičnom obore výrazu А.

Príklad 1 Prepíšme nerovnosť ako ekvivalentný systém racionálnych nerovností.

Podotýkam, že podmienky (1)–(4) sú podmienky pre doménu definície nerovnosti, ktorú odporúčam nájsť na začiatku riešenia.

Príklad 2 Riešte nerovnosť racionalizačnou metódou:

Oblasť definície nerovnosti je daná podmienkami:

Dostaneme:

Zostáva napísať nerovnosť (5)

Podlieha doméne

Odpoveď: (3; 5)

5. Konsolidácia študovaného materiálu

I. Napíšte nerovnosť ako systém racionálnych nerovností:

II. Vyjadrite pravú stranu nerovnosti vo forme logaritmu v požadovanom základe a prejdite na ekvivalentný systém:

Učiteľ zavolá na tabuľu žiakov, ktorí zapísali sústavy zo skupín I a II, a vyzve jedného z najsilnejších žiakov, aby domácu nerovnosť (č. 11,81 * a) vyriešil racionalizačnou metódou.

6. Overovacie práce

možnosť 1

Možnosť 2

1. Napíšte systém racionálnych nerovníc na riešenie nerovností:

2. Riešte nerovnosť racionalizačnou metódou

Kritériá hodnotenia:

3-4 body - "uspokojivé";
5-6 bodov - "dobré";
7 bodov - "výborne".

7. Reflexia

Odpovedzte na otázku: ktorá zo známych metód riešenia logaritmických nerovností s premenlivým základom vám umožní lepšie využiť čas na skúške?

8. Domáce úlohy:č.11,80 * (a, b), 11,81 * (a, b), 11,84 * (a, b) riešiť racionalizačnou metódou.

Bibliografia:

1. Algebra a začiatok analýzy: Proc. Pre 11 buniek. všeobecné vzdelanie Inštitúcie /[S.M. Nikolsky, M.K. Potapov, N.N. Rešetnikov, A.V. Shevkin] - 5. vydanie. - M.: Vzdelávanie, JSC "Moskvaské učebnice", 2006.
2. A.G. Koryanov, A.A. Prokofiev. Materiály kurzu „Príprava dobrých študentov a výborných študentov na skúšku“: prednášky 1.-4. - M .: Vysoká škola pedagogická „Prvý september“, 2012.