Помощь по Теле2, тарифы, вопросы

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).

См. также: Метод интегрирования по частям
Таблица неопределенных интегралов
Методы вычисления неопределенных интегралов
Основные элементарные функции и их свойства

Формула интегрирования по частям

При решении примеров этого раздела, используется формула интегрирования по частям:
;
.

Примеры интегралов, содержащих произведение многочлена и sin x, cos x или e x

Вот примеры таких интегралов:
, , .

Для интегрирования подобных интегралов, многочлен обозначают через u , а оставшуюся часть - через v dx . Далее применяют формулу интегрирования по частям.

Ниже дается подробное решение этих примеров.

Примеры решения интегралов

Пример с экспонентой, е в степени х

Определить интеграл:
.

Введем экспоненту под знак дифференциала:
e - x dx = - e - x d(-x) = - d(e - x) .

Интегрируем по частям.

здесь
.
Оставшийся интеграл также интегрируем по частям.
.
.
.
Окончательно имеем:
.

Пример определения интеграла с синусом

Вычислить интеграл:
.

Введем синус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 , v = cos(2 x+3) , du = ( x 2 )′ dx

Оставшийся интеграл также интегрируем по частям. Для этого вводим косинус под знак дифференциала.


здесь u = x , v = sin(2 x+3) , du = dx

Окончательно имеем:

Пример произведения многочлена и косинуса

Вычислить интеграл:
.

Введем косинус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 + 3 x + 5 , v = sin 2 x , du = ( x 2 + 3 x + 5)′ dx

Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций - интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы.

Стандартные методы интегрирования тригонометрических функций

Общий подход

Вначале, если это необходимо, подынтегральное выражение нужно преобразовать, чтобы тригонометрические функции зависели от одного аргумента, который совпадал бы с переменной интегрирования.

Например, если подынтегральное выражение зависит от sin(x+a) и cos(x+b) , то следует выполнить преобразование:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + sin ( x+a ) sin (b-a) .
После чего сделать замену z = x+a . В результате, тригонометрические функции будут зависеть только от переменной интегрирования z .

Когда тригонометрические функции зависят от одного аргумента, совпадающим с переменной интегрирования (допустим это z ), то есть подынтегральное выражение состоит только из функций типа sin z , cos z , tg z , ctg z , то нужно сделать подстановку
.
Такая подстановка приводит к интегрированию рациональных или иррациональных функций (если есть корни) и позволяет вычислить интеграл, если он интегрируется в элементарных функциях.

Однако, часто можно найти другие методы, которые позволяют вычислить интеграл более коротким способом, основываясь на специфике подынтегрального выражения. Ниже дано изложение основных таких методов.

Методы интегрирования рациональных функций от sin x и cos x

Рациональные функции от sin x и cos x - это функции, образованные из sin x , cos x и любых постоянных с помощью операций сложения, вычитания, умножения, деления и возведения в целочисленную степень. Они обозначаются так: R(sin x, cos x) . Сюда также могут входить тангенсы и котангенсы, поскольку они образованы делением синуса на косинус и наоборот.
Интегралы от рациональных функций имеют вид:
.

Методы интегрировании рациональных тригонометрических функций следующие.
1) Подстановка всегда приводит к интегралу от рациональной дроби. Однако, в некоторых случаях, существуют подстановки (они представлены ниже), которые приводят к более коротким вычислениям.
2) Если R(sin x, cos x) cos x → - cos x sin x .
3) Если R(sin x, cos x) умножается на -1 при замене sin x → - sin x , то выполняется подстановка t = cos x .
4) Если R(sin x, cos x) не меняется как при одновременной замене cos x → - cos x , и sin x → - sin x , то применяется подстановка t = tg x или t = ctg x .

Примеры:
, , .

Произведение степенных функций от cos x и sin x

Интегралы вида

являются интегралами от рациональных тригонометрических функций. Поэтому к ним можно применить методы, изложенные в предыдущем разделе. Ниже рассмотрены методы, основанные на специфике таких интегралов.

Если m и n - рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n - целые числа, то интегрирование выполняется с помощью формул приведения:

;
;
;
.

Пример:
.

Интегралы от произведения многочлена и синуса или косинуса

Интегралы вида:
, ,
где P(x) - многочлен от x , интегрируются по частям. При этом получаются следующие формулы:

;
.

Примеры:
, .

Интегралы от произведения многочлена, экспоненты и синуса или косинуса

Интегралы вида:
, ,
где P(x) - многочлен от x , интегрируются с помощью формулы Эйлера
e iax = cos ax + isin ax (где i 2 = -1 ).
Для этого методом, изложенном в предыдущем пункте, вычисляют интеграл
.
Выделив из результата действительную и мнимую часть, получают исходные интегралы.

Пример:
.

Нестандартные методы интегрирования тригонометрических функций

Ниже приведены ряд нестандартных методов, которые позволяют выполнить или упростить интегрирование тригонометрических функций.

Зависимость от (a sin x + b cos x)

Если подынтегральное выражение зависит только от a sin x + b cos x , то полезно применить формулу:
,
где .

Например

Разложение дроби из синусов и косинусов на более простые дроби

Рассмотрим интеграл
.
Наиболее простой способ интегрирования заключается в разложении дроби на более простые, применяя преобразование:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Интегрирование дробей первой степени

При вычислении интеграла
,
удобно выделить целую часть дроби и производную знаменателя
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Постоянные A и B находятся из сравнения левой и правой частей.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Таблица первообразных ("интегралов"). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.

Формулы интегрирования по частям. Правила интегрирования.

Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.

Если x - независимая переменная, то:

Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).

Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045…) ln(e)=1; ln(1)=0

Ряд Тейлора. Разложение функции в ряд Тейлора.

Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:

При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Ряд Тейлора в окрестности точки a имеет виды:

1) , где f(x) - функция, имеющая при х=а производные всех порядков. R n - остаточный член в ряде Тейлора определяется выражением

2)

k-тый коэффициент (при х k) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)

при a=0

члены ряда определяются по формуле

Условия применения рядов Тейлора.

1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.

Свойства рядов Тейлора.

Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.

Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации (приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis - линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.

Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.

Примеры некоторых распространенных разложений степенных функций в ряды Маклорена(=Макларена, Тейлора в окрестностях точки 0)

Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму

Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

Воспользовавшись известными тригонометрическими формулами

(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам

(5)

(6)

Пример 1. Найти

Решение. По формуле (2) при

Пример 2. Найти интеграл от тригонометрической функции

Решение. По формуле (3) при

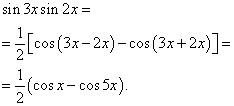
Пример 3. Найти интеграл от тригонометрической функции

Решение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:

Применяя формулу (6), получим

Интеграл произведения степеней синуса и косинуса одного и того же аргумента

Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

(7)

В частных случаях один из показателей (m или n ) может равняться нулю.

При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sin x dx ) .

Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.

Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что

Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t . Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx , выражая остальную часть подынтегральной функции через cos x и полагая t = cos x . Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса , когда хотя бы один из показателей - нечётный . Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения : когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.

Если же оба показателя m и n – чётные, то, используя тригонометрические формулы

понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится . Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.

Пример 4. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса – нечётный. Поэтому представим

t = sin x (тогда dt = cos x dx ). Тогда получим

Возвращаясь к старой переменной, окончательно найдём

Пример 5. Найти интеграл от тригонометрической функции

.

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим

и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим

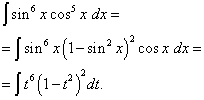
Раскроем скобки

и получим

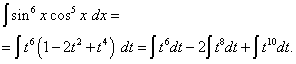
Возвращаясь к старой переменной, получаем решение

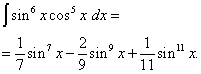
Пример 6. Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:

Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x . Тогда (1/2)dt = cos2x dx . Следовательно,

Окончательно получаем

Использование метода замены переменой

Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус - в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t , но и tgx = t и ctgx = t .

Пример 8. Найти интеграл от тригонометрической функции

.

Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:

.

Пример 9. Найти интеграл от тригонометрической функции

Решение. Преобразуем тангенс в отношение синуса и косинуса:

Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:

.

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Пример 10. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: , тогда .

Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :

Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt ). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение

Универсальная тригонометрическая подстановка

Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:

Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.

Пример 12. Найти интеграл от тригонометрической функции

.

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой . Тогда
.

Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда