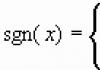Tele2 бойынша анықтама, тарифтер, сұрақтар

Бүгін, достар, ешқандай тоқырау мен сезім болмайды. Оның орнына мен сізді 8-9-сыныптардағы алгебра курсындағы ең қорқынышты қарсыластардың бірімен басқа сұрақтарсыз шайқасқа жіберемін.

Иә, сіз бәрін дұрыс түсіндіңіз: біз модулі бар теңсіздіктер туралы айтып отырмыз. Біз осы есептердің шамамен 90% шешуге болатын төрт негізгі әдісті қарастырамыз. Қалған 10% ше? Ал, біз олар туралы бөлек сабақта сөйлесеміз. :)

Дегенмен, ол жерде қандай да бір трюктерді талдамас бұрын, сіз білуіңіз керек екі фактіні еске түсіргім келеді. Әйтпесе, бүгінгі сабақтың материалын мүлде түсінбеу қаупі бар.

Сіз нені білуіңіз керек

Капитан Дәлел, модуль арқылы теңсіздіктерді шешу үшін екі нәрсені білу керек екенін айтады:

1. Теңсіздіктер қалай шешіледі?
2. Модуль дегеніміз не.

Екінші тармақтан бастайық.

Модуль анықтамасы

Мұнда бәрі қарапайым. Екі анықтама бар: алгебралық және графикалық. Алгебрадан бастайық:

Анықтама. $x$ санының модулі не теріс емес болса, санның өзі немесе бастапқы $x$ әлі теріс болса, оған қарама-қарсы сан болып табылады.

Ол былай жазылған:

\[\сол| x \right|=\left\( \бастау(туралау) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\соңы(туралау) \оңға.\]

Қарапайым тілмен айтқанда, модуль «минуссыз сан». Бұл екі жақтылықта (бір жерде бастапқы нөмірмен ештеңе істеудің қажеті жоқ, бірақ бір жерде минустарды жою керек) және жаңадан бастаған студенттер үшін барлық қиындықтар жатыр.

Сондай-ақ геометриялық анықтама бар. Оны білу де пайдалы, бірақ біз оған тек күрделі және кейбір ерекше жағдайларда ғана сілтеме жасаймыз, мұнда геометриялық тәсіл алгебралық тәсілге қарағанда ыңғайлы (спойлер: бүгін емес).

Анықтама. Нақты түзуде $a$ нүктесі белгіленсін. Содан кейін $\left| модулі x-a \right|$ — $x$ нүктесінен осы түзудің $a$ нүктесіне дейінгі қашықтық.

Егер сіз сурет салсаңыз, сіз келесідей нәрсені аласыз:

Графикалық модуль анықтамасы

Қалай болғанда да, оның негізгі қасиеті модуль анықтамасынан бірден шығады: санның модулі әрқашан теріс емес мән болып табылады. Бұл факт біздің бүгінгі бүкіл тарихымызда өтетін қызыл жіп болады.

Теңсіздіктерді шешу. Аралық әдіс

Енді теңсіздіктерді қарастырайық. Олардың көпшілігі бар, бірақ біздің ендігі міндетіміз олардың ең қарапайымын шеше білу. Сызықтық теңсіздіктерге, сонымен қатар интервалдар әдісіне келтірілгендер.

Менде бұл тақырып бойынша екі үлкен оқу құралы бар (айтпақшы, өте пайдалы - оқуды ұсынамын):

1. Теңсіздіктерге арналған интервал әдісі (әсіресе бейнені қараңыз);
2. Бөлшек-рационал теңсіздіктер өте көлемді сабақ, бірақ одан кейін сізде сұрақтар мүлде қалмайды.

Егер сіз мұның бәрін білсеңіз, егер «теңсіздіктен теңдеуге көшейік» деген тіркес сізді қабырғаға тіреліп өлтіргіңіз келмесе, онда сіз дайынсыз: сабақтың негізгі тақырыбына тозаққа қош келдіңіз. :)

1. «Функциядан кіші модуль» түріндегі теңсіздіктер

Бұл модульдермен жиі кездесетін тапсырмалардың бірі. Пішіннің теңсіздігін шешу үшін қажет:

\[\сол| f\right| \ltg\]

Кез келген нәрсе $f$ және $g$ функциялары ретінде әрекет ете алады, бірақ әдетте олар көпмүшеліктер болып табылады. Мұндай теңсіздіктердің мысалдары:

\[\бастау(туралау) & \left| 2x+3\оңға| \ltx+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\сол| x \right|-3 \right| \lt 2. \\\соңы(туралау)\]

Олардың барлығы схемаға сәйкес бір жолда сөзбе-сөз шешіледі:

\[\сол| f\right| \lt g\Оң жақ көрсеткі -g \lt f \lt g\quad \сол(\Оң жақ көрсеткі \сол\( \бастау(туралау) & f \lt g, \\ & f \gt -g \\\соңы(туралау) \right.\right)\]

Модульден құтылғанымызды көру оңай, бірақ оның орнына қос теңсіздік (немесе, бұл бірдей нәрсе, екі теңсіздіктер жүйесі) аламыз. Бірақ бұл көшу барлық мүмкін болатын мәселелерді толығымен ескереді: модуль астындағы сан оң болса, әдіс жұмыс істейді; теріс болса, ол әлі де жұмыс істейді; және $f$ немесе $g$ орнына ең жеткіліксіз функция болса да, әдіс жұмыс істей береді.

Әрине, сұрақ туындайды: бұл оңай емес пе? Өкінішке орай, мүмкін емес. Бұл модульдің барлық мәні.

Бірақ философиялау жеткілікті. Бір-екі мәселені шешейік:

Тапсырма. Теңсіздікті шеш:

\[\сол| 2x+3\оңға| \ltx+7\]

Шешім. Сонымен, бізде «модуль кем» түріндегі классикалық теңсіздік бар - тіпті түрлендіруге ештеңе жоқ. Біз алгоритм бойынша жұмыс істейміз:

\[\бастау(туралау) & \left| f\right| \lt g\Оң жақ көрсеткі -g \lt f \lt g; \\ & \left| 2x+3\оңға| \lt x+7\Оң жақ көрсеткі -\сол(x+7 \оң) \lt 2x+3 \lt x+7 \\\соңы(туралау)\]

Алдында «минус» бар жақшаларды ашуға асықпаңыз: асығыстың салдарынан сіз қателесуіңіз мүмкін.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\сол\( \бастау(туралау) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \соңы(туралау) \оңға.\]

\[\сол\( \бастау(туралау) & -3x \lt 10 \\ & x \lt 4 \\ \соңы(туралау) \оңға.\]

\[\сол\( \бастау(туралау) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \соңы(туралау) \оңға.\]

Мәселе екі қарапайым теңсіздікке дейін қысқартылды. Олардың шешімдерін параллель нақты түзулер бойынша белгілейміз:

Көптің қиылысы

Осы жиындардың қиылысы жауап болады.

Жауабы: $x\in \left(-\frac(10)(3);4 \right)$

Тапсырма. Теңсіздікті шеш:

\[\сол| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Шешім. Бұл тапсырма сәл қиынырақ. Бастау үшін біз екінші терминді оңға жылжыту арқылы модульді оқшаулаймыз:

\[\сол| ((x)^(2))+2x-3 \оң| \lt -3\сол(x+1 \оң)\]

Әлбетте, бізде қайтадан «модуль аз» пішінінің теңсіздігі бар, сондықтан біз бұрыннан белгілі алгоритмге сәйкес модульден құтыламыз:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \оң)\]

Енді назар аударыңыз: біреу мені осы жақшалардың бәрімен аздап бұзық деп айтады. Бірақ біздің басты мақсатымыз екенін тағы бір рет еске саламын теңсіздікті дұрыс шешіп, жауабын алады. Кейінірек, сіз осы сабақта сипатталғанның бәрін жақсы меңгерген кезде, өзіңізді қалағаныңызша бұрмалауға болады: жақшаларды ашыңыз, минустарды қосыңыз және т.б.

Жаңадан бастағандар үшін біз сол жақтағы қос минустан құтыламыз:

\[-\сол(-3\сол(x+1 \оң) \оң)=\сол(-1 \оң)\cdot \left(-3 \оң)\cdot \сол(x+1 \оң) =3\сол(x+1\оң)\]

Енді қос теңсіздіктегі барлық жақшаларды ашайық:

Екі еселенген теңсіздікке көшейік. Бұл жолы есептеулер маңыздырақ болады:

\[\left\( \бастау(туралау) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \соңы(туралау) \оңға.\]

\[\left\( \begin(туралау) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( туралау)\оңға.\]

Екі теңсіздік те квадрат және интервал әдісімен шешіледі (сол себепті айтамын: егер оның не екенін білмесеңіз, әлі модульдерді қабылдамағаныңыз жөн). Бірінші теңсіздіктегі теңдеуге өтеміз:

\[\бастау(туралау) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\соңы(туралау)\]

Көріп отырғаныңыздай, шығыс элементар түрде шешілетін толық емес квадрат теңдеу болып шықты. Енді жүйенің екінші теңсіздігін қарастырайық. Мұнда сіз Виетаның теоремасын қолдануыңыз керек:

\[\бастау(туралау) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\соңы(туралау)\]

Алынған сандарды екі параллель түзуде белгілейміз (бірінші теңсіздік үшін бөлек, екіншісі үшін бөлек):

Тағы да, біз теңсіздіктер жүйесін шешіп жатқандықтан, бізді көлеңкеленген жиындардың қиылысуы қызықтырады: $x\in \left(-5;-2 \right)$. Бұл жауап.

Жауабы: $x\in \left(-5;-2 \right)$

Менің ойымша, осы мысалдардан кейін шешім схемасы өте анық:

1. Барлық басқа мүшелерді теңсіздіктің қарама-қарсы жағына жылжыту арқылы модульді оқшаулаңыз. Осылайша $\left| түріндегі теңсіздікті аламыз f\right| \ltg$.
2. Жоғарыда сипатталғандай модульден құтылу арқылы осы теңсіздікті шешіңіз. Бір сәтте қос теңсіздіктен әрқайсысын жеке шешуге болатын екі тәуелсіз өрнектер жүйесіне көшу қажет болады.
3. Ақырында, осы екі тәуелсіз өрнектің шешімдерін кесіп өту ғана қалады - және бұл аяқталды, біз түпкілікті жауапты аламыз.

Ұқсас алгоритм модуль функциядан үлкен болғанда келесі түрдегі теңсіздіктер үшін бар. Дегенмен, бірнеше маңызды «бірақ» бар. Біз қазір осы «бірақ» туралы сөйлесетін боламыз.

2. «Модуль функциядан үлкен» түріндегі теңсіздіктер

Олар келесідей көрінеді:

\[\сол| f\right| \gt g\]

Алдыңғыға ұқсас па? Сияқты. Дегенмен, мұндай міндеттер мүлдем басқа жолмен шешіледі. Ресми түрде схема келесідей:

\[\сол| f\right| \gt g\Оң жақ көрсеткі \left[ \begin(туралау) & f \gt g, \\ & f \lt -g \\\end(туралау) \оңға.\]

Басқаша айтқанда, біз екі жағдайды қарастырамыз:

1. Біріншіден, біз жай ғана модульді елемейміз - біз әдеттегі теңсіздікті шешеміз;
2. Содан кейін, шын мәнінде, біз минус таңбасы бар модульді ашамыз, содан кейін теңсіздіктің екі бөлігін −1-ге, таңбамен көбейтеміз.

Бұл жағдайда опциялар төртбұрышты жақшамен біріктіріледі, яғни. Бізде екі талаптың жиынтығы бар.

Тағы да назар аударыңыз: біздің алдымызда жүйе емес, жиынтық жауапта жиындар қиылысқан емес, біріктірілген. Бұл алдыңғы абзацтан түбегейлі айырмашылығы!

Тұтастай алғанда, көптеген студенттер кәсіподақтар мен қиылыстармен көп шатасады, сондықтан бұл мәселені біржола қарастырайық:

• «∪» жалғау белгісі. Шын мәнінде, бұл ағылшын тілінен бізге келген стильдендірілген «U» әрпі және «Union» аббревиатурасы, яғни. «Ассоциациялар».
• "∩" - қиылысу белгісі. Бұл сұмдық еш жерден шыққан жоқ, тек «∪» дегенге қарсылық ретінде пайда болды.

Есте сақтауды жеңілдету үшін көзілдірік жасау үшін осы белгілерге аяқтарды қосыңыз (тек қазір мені нашақорлық пен алкоголизмді насихаттады деп айыптамаңыз: егер сіз бұл сабақты шындап оқып жатсаңыз, онда сіз есірткіге тәуелдісіз):

Жиындардың қиылысуы мен бірігуінің айырмашылығы

Орыс тіліне аударғанда бұл мынаны білдіреді: одақ (жинақ) екі жиынның элементтерін қамтиды, сондықтан олардың әрқайсысынан кем емес; бірақ қиылысу (жүйе) бірінші жиында да, екіншісінде де болатын элементтерді ғана қамтиды. Сондықтан жиындардың қиылысуы ешқашан бастапқы жиындардан үлкен болмайды.

Сонда ол түсінікті болды ма? Міне керемет. Жаттығуға көшейік.

Тапсырма. Теңсіздікті шеш:

\[\сол| 3x+1 \оңға| \gt 5-4x\]

Шешім. Біз схемаға сәйкес әрекет етеміз:

\[\сол| 3x+1 \оңға| \gt 5-4x\Оң жақ көрсеткі \left[ \бастау(туралау) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \оң) \\\соңы(туралау) \ дұрыс.\]

Әрбір халық теңсіздігін шешеміз:

\[\left[ \begin(туралау) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(туралау) \оңға.\]

\[\left[ \begin(туралау) & 7x \gt 4 \\ & -x \lt -6 \\ \end(туралау) \оңға.\]

\[\left[ \begin(туралау) & x \gt 4/7\ \\ & x \gt 6 \\ \end(туралау) \оңға.\]

Әрбір нәтиже жиынын сандар жолында белгілеп, содан кейін оларды біріктіреміз:

Жиындар одағы

Жауап $x\in \left(\frac(4)(7);+\infty \right)$ екені анық.

Жауабы: $x\in \left(\frac(4)(7);+\infty \right)$

Тапсырма. Теңсіздікті шеш:

\[\сол| ((x)^(2))+2x-3 \оң| \gtx\]

Шешім. Енді не? Жоқ, бәрі бірдей. Модульі бар теңсіздіктен екі теңсіздіктер жиынына көшеміз:

\[\сол| ((x)^(2))+2x-3 \оң| \gt x\Оң жақ көрсеткі \left[ \begin(туралау) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\соңы(туралау) \оңға.\]

Әрбір теңсіздікті шешеміз. Өкінішке орай, онда тамырлар өте жақсы болмайды:

\[\бастау(туралау) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\соңы(туралау)\]

Екінші теңсіздікте де аздап ойын бар:

\[\бастау(туралау) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\соңы(туралау)\]

Енді біз бұл сандарды екі осьте белгілеуіміз керек - әрбір теңсіздік үшін бір ось. Дегенмен, нүктелерді дұрыс ретпен белгілеу керек: сан неғұрлым көп болса, нүкте соғұрлым оңға қарай жылжиды.

Міне, біз орнатуды күтеміз. $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ сандарымен бәрі түсінікті болса (бірінші алымдағы терминдер бөлшек екіншінің алымындағы мүшелерден аз, сондықтан қосынды да кішірек, $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt) (21))(2)$ да ешқандай қиындық болмайды (оң сан теріс екені анық), бірақ соңғы жұппен бәрі оңай емес. Қайсысы үлкен: $\frac(-3+\sqrt(21))(2)$ немесе $\frac(-1+\sqrt(13))(2)$? Сандық сызықтардағы нүктелердің орналасуы және шын мәнінде жауап осы сұрақтың жауабына байланысты болады.

Ендеше салыстырайық:

\[\бастау(матрица) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\соңы(матрица)\]

Біз түбірді бөліп алдық, теңсіздіктің екі жағында да теріс емес сандарды алдық, сондықтан екі жағын да шаршылауға құқығымыз бар:

\[\begin(матрица) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(матрица)\]

Менің ойымша, бұл $4\sqrt(13) \gt 3$, сондықтан $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, соңында осьтердегі нүктелер келесідей орналасады:

Ұсқынсыз тамырлардың жағдайы

Еске сала кетейін, біз жиынды шешіп жатырмыз, сондықтан жауап көлеңкелі жиындардың қиылысы емес, бірігу болады.

Жауабы: $x\in \left(-\infty;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2) );+\infty\right)$

Көріп отырғаныңыздай, біздің схема қарапайым тапсырмалар үшін де, өте қиын тапсырмалар үшін де жақсы жұмыс істейді. Бұл тәсілдегі жалғыз «әлсіз жер» - иррационал сандарды дұрыс салыстыру керек (және маған сеніңіз: бұл тек тамырлар ғана емес). Бірақ бөлек (және өте маңызды сабақ) салыстыру сұрақтарына арналады. Ал біз әрі қарай жүреміз.

3. Теріс емес «құйрықтары» бар теңсіздіктер

Сонымен біз ең қызығына жеттік. Бұл пішіннің теңсіздіктері:

\[\сол| f\right| \gt\left| g\right|\]

Жалпы айтқанда, қазір біз айтатын алгоритм тек модульге қатысты. Ол сол және оң жақта кепілдік берілген теріс емес өрнектер бар барлық теңсіздіктерде жұмыс істейді:

Бұл тапсырмалармен не істеу керек? Тек есте сақтаңыз:

Теріс емес құйрықтары бар теңсіздіктерде екі жағы да кез келген табиғи қуатқа көтерілуі мүмкін. Қосымша шектеулер болмайды.

Ең алдымен, бізді квадраттау қызықтырады - ол модульдер мен түбірлерді күйдіреді:

\[\бастау(туралау) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\соңы(туралау)\]

Мұны квадраттың түбірін алумен шатастырмаңыз:

\[\sqrt(((f)^(2)))=\сол| f \right|\ne f\]

Студент модуль орнатуды ұмытып кеткенде сансыз қателіктер жіберілді! Бірақ бұл мүлдем басқа әңгіме (бұл иррационал теңдеулер сияқты), сондықтан біз оған енді кірмейміз. Бірнеше мәселені жақсырақ шешейік:

Тапсырма. Теңсіздікті шеш:

\[\сол| x+2 \right|\ge \left| 1-2x \оңға|\]

Шешім. Біз бірден екі нәрсені байқаймыз:

1. Бұл қатаң емес теңсіздік. Сан сызығындағы нүктелер тесіліп алынады.
2. Теңсіздіктің екі жағы да теріс емес екені анық (бұл модульдің қасиеті: $\left| f\left(x \right) \right|\ge 0$).

Демек, модульден құтылу үшін теңсіздіктің екі жағын да квадраттай аламыз және мәселені әдеттегі интервал әдісімен шеше аламыз:

\[\бастау(туралау) & ((\сол(\сол| x+2 \оң| \оң))^(2))\ge ((\left(\сол| 1-2x \оң| \оң)) )^(2)); \\ & ((\сол(x+2 \оң))^(2))\ge ((\left(2x-1 \оң))^(2)). \\\соңы(туралау)\]

Соңғы қадамда мен аздап алдадым: модульдің паритеті арқылы терминдер тізбегін өзгерттім (шын мәнінде мен $1-2x$ өрнегін −1-ге көбейттім).

\[\бастау(туралау) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ right)\right)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(туралау)\]

Интервал әдісімен шешеміз. Теңсіздіктен теңдеуге көшейік:

\[\бастау(туралау) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\соңы(туралау)\]

Табылған түбірлерді сан сызығына белгілейміз. Тағы да: барлық нүктелер көлеңкеленген, себебі бастапқы теңсіздік қатаң емес!

Модуль белгісінен құтылу

Ерекше қыңырлар үшін еске сала кетейін: біз теңдеуге көшкенге дейін жазылған соңғы теңсіздіктен белгілерді аламыз. Және сол теңсіздікте қажетті аумақтарды бояймыз. Біздің жағдайда бұл $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Сонымен бітті. Мәселе шешілді.

Жауабы: $x\in \left[ -\frac(1)(3);3 \right]$.

Тапсырма. Теңсіздікті шеш:

\[\сол| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \оң|\]

Шешім. Біз бәрін бірдей жасаймыз. Мен түсініктеме бермеймін - тек әрекеттер тізбегін қараңыз.

Оны квадраттайық:

\[\бастау(туралау) & ((\left(\left| ((x)^(2))+x+1 \оң| \оң))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \оңға| \оңға))^(2)); \\ & ((\left(((x)^(2))+x+1 \оң))^(2))\le ((\left(((x)^(2))+3x+4 \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \оң))^(2))-((\left(((x)^(2))+3x+4 \ оң жақ))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x)) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\соңы(туралау)\]

Аралықты бөлу әдісі:

\[\бастау(туралау) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Оң жақ көрсеткі x=-1,5; \\ & 2((x)^(2))+4x+5=0\Оң жақ көрсеткі D=16-40 \lt 0\Оң жақ көрсеткі \varnothing . \\\соңы(туралау)\]

Сан түзуінде бір ғана түбір бар:

Жауап - тұтас диапазон

Жауабы: $x\in \left[ -1,5;+\infty \right)$.

Соңғы тапсырма туралы шағын ескерту. Менің студенттерімнің бірі дәл атап өткендей, бұл теңсіздіктегі екі ішкі модуль өрнектері де оң, сондықтан модуль белгісін денсаулыққа зиян келтірместен өткізіп жіберуге болады.

Бірақ бұл қазірдің өзінде мүлдем басқа ойлау деңгейі және басқа көзқарас - оны шартты түрде салдар әдісі деп атауға болады. Ол туралы - бөлек сабақта. Ал енді бүгінгі сабақтың қорытынды бөліміне өтіп, әрқашан жұмыс істейтін әмбебап алгоритмді қарастырайық. Барлық алдыңғы тәсілдер күшсіз болған кезде де. :)

4. Опцияларды санамалау әдісі

Егер бұл айлалардың бәрі жұмыс істемесе ше? Егер теңсіздік теріс емес құйрықтарға дейін төмендемесе, модульді оқшаулау мүмкін болмаса, егер мүлде ауырсыну-мұңды-сағыныш болса?

Содан кейін сахнаға барлық математиканың «ауыр артиллериясы» кіреді - санау әдісі. Модульмен теңсіздіктерге келетін болсақ, ол келесідей болады:

1. Барлық ішкі модуль өрнектерін жазыңыз және оларды нөлге теңестіріңіз;
2. Алынған теңдеулерді шешіп, бір сан түзуіне табылған түбірлерді белгілеу;
3. Түзу сызық бірнеше бөліктерге бөлінеді, олардың ішінде әрбір модульдің бекітілген белгісі бар, сондықтан бір мәнді түрде кеңейеді;
4. Әрбір осындай бөлім бойынша теңсіздікті шешіңіз (сенімділік үшін 2-тармақта алынған шекаралық түбірлерді бөлек қарастыруға болады). Нәтижелерді біріктіріңіз - бұл жауап болады. :)

Қалай? Әлсіз бе? Оңай! Тек ұзақ уақытқа. Іс жүзінде көрейік:

Тапсырма. Теңсіздікті шеш:

\[\сол| x+2 \оң| \lt\left| x-1 \right|+x-\frac(3)(2)\]

Шешім. Бұл ақымақтық $\left| сияқты теңсіздіктерге әкелмейді f\right| \lt g$, $\left| f\right| \gt g$ немесе $\left| f\right| \lt\left| g \right|$, ендеше әрі қарай жүрейік.

Біз субмодульдік өрнектерді жазамыз, оларды нөлге теңеп, түбірін табамыз:

\[\бастау(туралау) & x+2=0\Оң жақ көрсеткі x=-2; \\ & x-1=0\Оң жақ көрсеткі x=1. \\\соңы(туралау)\]

Барлығы бізде сан сызығын үш бөлікке бөлетін екі түбір бар, олардың ішінде әрбір модуль бірегей түрде ашылады:

Ішкі модульдік функциялардың сандар жолын нөлге бөлу

Әр бөлімді бөлек қарастырайық.

1. $x \lt -2$ болсын. Сонда екі ішкі модуль өрнектері де теріс болады және бастапқы теңсіздік келесідей қайта жазылады:

\[\бастау(туралау) & -\сол(x+2 \оң) \lt -\сол(x-1 \оң)+x-1,5 \\ & -x-2 \lt -x+1+ x-1,5 \\ & x \gt 1,5 \\\соңы(туралау)\]

Бізде қарапайым шектеулер бар. Оны $x \lt -2$ болатын бастапқы болжаммен қиып көрейік:

\[\сол\( \бастау(туралау) & x \lt -2 \\ & x \gt 1,5 \\\соңы(туралау) \оңға.\Оң жақ көрсеткі x\ \varnothing \]

$x$ айнымалысы бір уақытта −2-ден кіші, бірақ 1,5-тен үлкен болуы мүмкін емес екені анық. Бұл салада шешімдер жоқ.

1.1. Шекаралық жағдайды бөлек қарастырайық: $x=-2$. Осы санды бастапқы теңсіздікке ауыстырайық және тексерейік: ол орындалады ма?

\[\бастау(туралау) & ((\сол. \сол| x+2 \оң| \lt \сол| x-1 \оң|+x-1,5 \оң|)_(x=-2) ) \\ & 0 \lt \сол| -3 \right|-2-1,5; \\ & 0 \лт 3-3,5; \\ & 0 \lt -0,5\Оң жақ көрсеткі \varnothing . \\\соңы(туралау)\]

Есептер тізбегі бізді қате теңсіздікке әкелгені анық. Демек, бастапқы теңсіздік те жалған және $x=-2$ жауапқа қосылмайды.

2. Енді $-2 \lt x \lt 1$ болсын. Сол жақ модуль қазірдің өзінде «плюс» арқылы ашылады, бірақ оң жақта «минус» бар. Бізде бар:

\[\бастау(туралау) & x+2 \lt -\сол(x-1 \оң)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2.5 \\\соңы(туралау)\]

Біз қайтадан бастапқы талаппен қиылысамыз:

\[\сол\( \бастау(туралау) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\соңы(туралау) \оңға.\Оң жақ көрсеткі x\ \varештеңеде \]

Және тағы да, шешімдердің бос жиыны, өйткені −2,5-тен кіші және −2-ден үлкен сандар жоқ.

2.1. Тағы да ерекше жағдай: $x=1$. Бастапқы теңсіздікті ауыстырамыз:

\[\бастау(туралау) & ((\сол. \сол| x+2 \оң| \lt \сол| x-1 \оң|+x-1,5 \оң|)_(x=1)) \\ & \left| 3\оңға| \lt\left| 0 \right|+1-1,5; \\ & 3 \лт -0,5; \\ & 3 \lt -0,5\Оң жақ көрсеткі \varnothing . \\\соңы(туралау)\]

Алдыңғы «ерекше жағдай» сияқты $x=1$ саны жауапта анық емес.

3. Жолдың соңғы бөлігі: $x \gt 1$. Мұнда барлық модульдер плюс белгісімен кеңейтілген:

\[\бастау(туралау) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \соңында(туралау)\ ]

Біз қайтадан табылған жиынды бастапқы шектеумен қиылысамыз:

\[\сол\( \бастау(туралау) & x \gt 4,5 \\ & x \gt 1 \\\соңы(туралау) \оңға.\Оң жақ көрсеткі x\солға(4,5;+\infty) \right)\]

Әйтеуір! Біз интервалды таптық, ол жауап болады.

Жауабы: $x\in \left(4,5;+\infty \right)$

Соңында, нақты мәселелерді шешу кезінде сізді ақымақ қателіктерден құтқаратын бір ескерту:

Модульдері бар теңсіздіктердің шешімдері әдетте сандар түзуіндегі үзіліссіз жиындар – интервалдар мен кесінділер болып табылады. Оқшауланған нүктелер әлдеқайда сирек кездеседі. Және одан да сирек, шешімнің шекаралары (сегменттің соңы) қарастырылатын диапазонның шекарасымен сәйкес келеді.

Сондықтан, егер шекаралар («ерекше жағдайлар») жауапқа қосылмаса, онда бұл шекаралардың сол-оң жағындағы аумақтар да жауапқа қосылмайды. Және керісінше: шекара жауап ретінде кірді, яғни оның айналасындағы кейбір аймақтар да жауаптар болады.

Шешімдерді тексерген кезде мұны есте сақтаңыз.

Ал бүгінде ұтымды теңсіздіктерді әркім шеше алмайды. Дәлірек айтқанда, әркім ғана шеше алмайды. Мұны аз адамдар жасай алады.
Кличко

Бұл сабақ қиын болады. Оның соңына Таңдалғандар ғана жетеді. Сондықтан, оқымас бұрын мен әйелдерді, мысықтарды, жүкті балаларды және ...

Жарайды, бұл өте қарапайым. Сіз интервал әдісін игердіңіз делік (егер оны меңгермеген болсаңыз, қайта оралып, оны оқуға кеңес беремін) және $P\left(x \right) \gt 0$ түріндегі теңсіздіктерді шешуді үйрендіңіз, мұндағы $P \left(x \right)$ - кейбір көпмүшелік немесе көпмүшелердің көбейтіндісі.

Сізге шешу қиын болмайды деп ойлаймын, мысалы, мұндай ойын (айтпақшы, оны қыздыру үшін көріңіз):

\[\begin(align) & \left(2((x)^(2))+3x+4 \right)\left(4x+25 \right) \gt 0; \\ & x\left(2((x)^(2))-3x-20 \right)\left(x-1 \right)\ge 0; \\ & \left(8x-((x)^(4)) \right)((\left(x-5 \right))^(6))\le 0. \\ \end(туралау)\]

Енді тапсырманы аздап қиындатып, тек көпмүшелерді ғана емес, форманың рационал бөлшектерін де қарастырайық:

мұндағы $P\left(x \right)$ және $Q\left(x \right)$ $((a)_(n))((x)^(n))+( түріндегі бірдей көпмүшеліктер. ( a)_(n-1))((x)^(n-1))+...+((a)_(0))$ немесе осындай көпмүшелердің көбейтіндісі.

Бұл рационалды теңсіздік болады. Негізгі нүкте - азайғышта $x$ айнымалысының болуы. Мысалы, рационал теңсіздіктер:

\[\бастау(туралау) & \frac(x-3)(x+7) \lt 0; \\ & \frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0; \\ & \frac(3((x)^(2))+10x+3)(((\left(3-x \right))^(2))\left(4-((x)^( 2)) \оңға))\ge 0. \\ \соңы(туралау)\]

Және бұл рационал емес, интервал әдісімен шешілетін ең көп таралған теңсіздік:

\[\frac(((x)^(2))+6x+9)(5)\ge 0\]

Алға қарай отырып, мен бірден айтамын: ұтымды теңсіздіктерді шешудің кем дегенде екі жолы бар, бірақ олардың барлығы бір жолмен бізге бұрыннан белгілі интервалдар әдісіне келтірілген. Сондықтан бұл әдістерді талдамас бұрын, ескі фактілерді еске түсірейік, әйтпесе жаңа материалдан ешқандай мағына болмайды.

Сіз нені білуіңіз керек

Маңызды фактілер көп емес. Бізге тек төртеуі керек.

Қысқартылған көбейту формулалары

Иә, иә: олар бізді мектептегі математикалық оқу бағдарламасы бойынша қудалайды. Және университетте де. Бұл формулалардың бірнешеуі бар, бірақ бізге мыналар ғана қажет:

\[\бастау(туралау) & ((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \оңға))^(2)); \\ & ((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right); \\ & ((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b) ^(2))\оң жақ); \\ & ((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+(b)^( 2))\оңға). \\ \соңы(туралау)\]

Соңғы екі формулаға назар аударыңыз - бұл текшелердің қосындысы мен айырмасы (соның немесе айырмашылықтың кубы емес!). Бірінші жақшадағы белгі бастапқы өрнектегі таңбамен бірдей, ал екінші жақшадағы бастапқы өрнектегі белгіге қарама-қарсы екенін байқасаңыз, оларды есте сақтау оңай.

Сызықтық теңдеулер

Бұл $ax+b=0$ түріндегі ең қарапайым теңдеулер, мұнда $a$ және $b$ жай сандар және $a\ne 0$. Бұл теңдеуді шешу оңай:

\[\бастау(туралау) & ax+b=0; \\ &ax=-b; \\ & x=-\frac(b)(a). \\ \соңы(туралау)\]

$a$ коэффициентіне бөлуге құқығымыз бар екенін ескертемін, себебі $a\ne 0$. Бұл талап өте қисынды, өйткені $a=0$ арқылы біз мынаны аламыз:

Біріншіден, бұл теңдеуде $x$ айнымалысы жоқ. Бұл, жалпы айтқанда, бізді шатастырмауы керек (бұл, айталық, геометрияда және жиі кездеседі), бірақ бәрібір біз енді сызықтық теңдеу емеспіз.

Екіншіден, бұл теңдеудің шешімі тек $b$ коэффициентіне байланысты. Егер $b$ да нөл болса, онда біздің теңдеу $0=0$ болады. Бұл теңдік әрқашан дұрыс; демек $x$ - кез келген сан (әдетте \mathbb(R)$ ішінде $x\ түрінде жазылады). Егер $b$ коэффициенті нөлге тең болмаса, онда $b=0$ теңдігі ешқашан орындалмайды, яғни. жауаптар жоқ (\varnothing $ ішінде $x\ деп жазылып, "шешімдер жинағы бос" деп оқыңыз).

Барлық осы күрделіліктерді болдырмау үшін біз жай ғана $a\ne 0$ деп есептейміз, бұл бізді әрі қарай ой жүгіртуден ешбір жағдайда шектемейді.

Квадрат теңдеулер

Естеріңізге сала кетейін, бұл квадрат теңдеу деп аталады:

Мұнда сол жақта екінші дәрежелі көпмүше, тағы да $a\ne 0$ (әйтпесе квадрат теңдеудің орнына сызықтық теңдеуді аламыз). Дискриминант арқылы келесі теңдеулер шешіледі:

1. $D \gt 0$ болса, екі түрлі түбір аламыз;
2. Егер $D=0$ болса, онда түбір бір, бірақ екінші еселік болады (ол қандай көптік және оны қалай ескеру керек - бұл туралы кейінірек). Немесе теңдеудің екі бірдей түбірі бар деп айта аламыз;
3. $D \lt 0$ үшін түбірлер мүлде жоқ, кез келген $x$ үшін $a((x)^(2))+bx+c$ көпмүшесінің таңбасы $a коэффициентінің таңбасымен сәйкес келеді. $. Бұл, айтпақшы, қандай да бір себептермен алгебра сабақтарында айтуды ұмытып кеткен өте пайдалы факт.

Тамырлардың өзі белгілі формула бойынша есептеледі:

\[((x)_(1,2))=\frac(-b\pm \sqrt(D))(2a)\]

Демек, дискриминантқа қатысты шектеулер. Өйткені, теріс санның квадрат түбірі жоқ. Түбірлерге келетін болсақ, көптеген студенттердің бастарында қорқынышты тәртіпсіздік бар, сондықтан мен бүкіл сабақты арнайы жаздым: алгебрадағы түбір дегеніміз не және оны қалай есептеу керек - мен оны оқуды ұсынамын. :)

Рационал бөлшектермен амалдар

Жоғарыда жазылғандардың барлығы, сіз интервалдар әдісін зерттегеніңізді білесіз. Бірақ біз қазір талдайтын нәрсенің бұрын аналогы жоқ - бұл мүлдем жаңа факт.

Анықтама. Рационал бөлшек форманың өрнегі болып табылады

\[\frac(P\left(x \оң))(Q\сол(x \оң))\]

мұндағы $P\left(x \right)$ және $Q\left(x \right)$ полиномдар.

Мұндай бөлшектен теңсіздікті алу оңай екені анық - оңға «үлкен» немесе «кем» белгісін қою жеткілікті. Ал сәл әрі қарай біз мұндай мәселелерді шешудің рахат екенін көреміз, онда бәрі өте қарапайым.

Есептер бір өрнекте бірнеше осындай бөлшек болғанда басталады. Оларды ортақ бөлгішке дейін азайту керек - дәл осы сәтте көптеген шабуыл қателері жіберіледі.

Сондықтан рационал теңдеулерді сәтті шешу үшін екі дағдыны берік меңгеру қажет:

1. $P\left(x \right)$ көпмүшені көбейткіштерге бөлу;
2. Шын мәнінде, бөлшектерді ортақ бөлгішке келтіру.

Көпмүшені көбейткіштерге қалай бөлуге болады? Өте оңай. Пішіннің көпмүшесі болсын

Оны нөлге теңестірейік. $n$-ші дәрежелі теңдеуді аламыз:

\[((a)_(n))((x)^(n))+((a)_(n-1))((x)^(n-1))+...+(( a)_(1))x+((a)_(0))=0\]

Бұл теңдеуді шешіп, $((x)_(1)),\ ...,\ ((x)_(n))$ түбірлерін алдық делік (уайымдамаңыз: көп жағдайда болмайды. осы түбірлердің екеуінен көп). Бұл жағдайда бастапқы көпмүшені келесідей қайта жазуға болады:

\[\бастау(туралау) & P\left(x \right)=((a)_(n))((x)^(n))+(a)_(n-1))((x) )^(n-1))+...+((a)_(1))x+((a)_(0))= \\ & =(a)_(n))\left(x -((x)_(1)) \оңға)\cdot \left(x-((x)_(2)) \оңға)\cdot ...\cdot \left(x-((x)_( n)) \оңға) \соңы(туралау)\]

Осымен болды! Назар аударыңыз: $((a)_(n))$ жетекші коэффициенті еш жерде жоғалған жоқ - бұл жақшалардың алдында бөлек фактор болады және қажет болған жағдайда оны осы жақшалардың кез келгеніне енгізуге болады (практикалық шоулар). $((a)_ (n))\ne \pm 1$ арқылы түбірлер арасында әрқашан дерлік бөлшектер бар).

Тапсырма. Өрнекті жеңілдету:

\[\frac(((x)^(2))+x-20)(x-4)-\frac(2((x)^(2))-5x+3)(2x-3)-\ frac(4-8x-5((x)^(2)(x+2)\]

Шешім. Алдымен бөлгіштерді қарастырайық: олардың барлығы сызықтық биномдар және мұнда көбейткіштерге бөлуге ештеңе жоқ. Ендеше алымдарды көбейткіштерге жіктейік:

\[\бастау(туралау) & ((x)^(2))+x-20=\left(x+5 \right)\left(x-4 \right); \\ & 2((x)^(2))-5x+3=2\сол(x-\frac(3)(2) \оң)\сол(x-1 \оң)=\сол(2x- 3\оң)\сол(x-1\оң); \\ & 4-8x-5((x)^(2))=-5\сол(x+2 \оң)\сол(x-\frac(2)(5) \оң)=\сол(x +2 \оңға)\солға(2-5x \оңға). \\\соңы(туралау)\]

Назар аударыңыз: екінші көпмүшеде «2» жоғары коэффициенті, біздің схемаға толық сәйкес, алдымен жақшаның алдында пайда болды, содан кейін бірінші жақшаға қосылды, өйткені бөлшек сол жерден шықты.

Үшінші көпмүшеде де солай болды, тек сонда ғана терминдердің реті де шатастырылған. Дегенмен, «−5» коэффициенті екінші жақшаға қосылды (есіңде болсын: факторды бір және бір жақшаға енгізуге болады!), бұл бізді бөлшек түбірлерге байланысты қолайсыздықтан құтқарды.

Бірінші көпмүшеге келетін болсақ, онда бәрі қарапайым: оның түбірлері стандартты түрде дискриминант арқылы немесе Виета теоремасы арқылы ізделеді.

Бастапқы өрнекке оралайық және оны көбейткіштерге бөлінген алымдармен қайта жазайық:

\[\бастау(матрица) \frac(\сол(x+5 \оң)\сол(x-4 \оң))(x-4)-\frac(\сол(2x-3 \оң)\сол( x-1 \оң))(2x-3)-\frac(\сол(x+2 \оң)\сол(2-5x \оң))(x+2)= \\ =\сол(x+5) \right)-\left(x-1 \right)-\left(2-5x \right)= \\ =x+5-x+1-2+5x= \\ =5x+4. \\ \соңы(матрица)\]

Жауабы: $5x+4$.

Көріп отырғаныңыздай, күрделі ештеңе жоқ. Біраз 7-8 сыныптың математикасы болды. Барлық түрлендірулердің мәні - күрделі және қорқынышты өрнекті қарапайым және жұмыс істеуге оңай нәрсеге айналдыру.

Дегенмен, бұл әрдайым бола бермейді. Ендеше, енді біз күрделі мәселені қарастырамыз.

Бірақ алдымен екі бөлшекті ортақ бөлгішке қалай жеткізуге болатынын анықтайық. Алгоритм өте қарапайым:

1. Бөлгіштердің екеуін де көбейткіштерге бөлу;
2. Бірінші бөлгішті қарастырып, оған біріншіде емес, екінші бөлгіште бар факторларды қосыңыз. Алынған өнім ортақ бөлгіш болады;
3. Бөлгіштер ортақ бөлшекке тең болу үшін бастапқы бөлшектердің әрқайсысында қандай көбейткіштер жетіспейтінін табыңыз.

Мүмкін, бұл алгоритм сізге «көп әріптер» бар мәтін сияқты көрінуі мүмкін. Сондықтан нақты мысалды қарастырайық.

Тапсырма. Өрнекті жеңілдету:

\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \оң)\cdot \left(\frac(((x)^(2))(((x)^(2))-4)- \frac(2)(2-x) \оңға)\]

Шешім. Мұндай көлемді тапсырмалар бөліктерде жақсы шешіледі. Бірінші жақшада не жазылғанын жазайық:

\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3))-8 )-\frac(1)(x-2)\]

Алдыңғы есептен айырмашылығы, мұнда бөлгіштер соншалықты қарапайым емес. Олардың әрқайсысын көбейткіштерге жіктейік.

$((x)^(2))+2x+4$ шаршы үшмүшені көбейткіштерге бөлуге болмайды, себебі $((x)^(2))+2x+4=0$ теңдеуінің түбірі жоқ (дискриминант теріс) . Біз оны өзгеріссіз қалдырамыз.

Екінші бөлгіш, текшелік көпмүшелік $((x)^(3))-8$, мұқият зерттегенде текшелердің айырмашылығы болып табылады және қысқартылған көбейту формулалары арқылы оңай бөлшектеуге болады:

\[((x)^(3))-8=((x)^(3))-((2)^(3))=\сол(x-2 \оң)\сол((x) ^(2))+2x+4 \оңға)\]

Басқа ештеңені көбейту мүмкін емес, өйткені бірінші жақшада сызықтық бином бар, ал екіншісінде бізге бұрыннан таныс, нақты түбірлері жоқ конструкция бар.

Ақырында, үшінші бөлгіш – бөлшектеуге болмайтын сызықтық бином. Осылайша, біздің теңдеу келесі формада болады:

\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\left(x-2 \оң)\сол (((x)^(2))+2x+4 \оң жақ))-\frac(1)(x-2)\]

$\left(x-2 \right)\left(((x)^(2))+2x+4 \right)$ ортақ бөлгіш болатыны анық және оған барлық бөлшектерді азайту үшін сіз бірінші бөлшекті $\left(x-2 \right)$, ал соңғысын $\left(((x)^(2))+2x+4 \right)$ көбейту керек. Содан кейін келесілерді әкелу ғана қалады:

\[\begin(матрица) \frac(x\cdot \left(x-2 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \ оң))+\frac(((x)^(2))+8)(\left(x-2 \right)\left(((x)^(2))+2x+4 \оң))- \frac(1\cdot \left(((x)^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x +4 \right))= \\ =\frac(x\cdot \left(x-2 \right)+\left(((x)^(2))+8 \right)-\left(((x) )^(2))+2x+4 \оң))(\сол(x-2 \оң)\сол(((x)^(2))+2x+4 \оң))= \\ =\frac (((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \оң)\сол (((x)^(2))+2x+4 \оңға))= \\ =\frac(((x)^(2))-4x+4)(\left(x-2 \оң)\ сол жақ(((x)^(2))+2x+4 \оңға)). \\ \соңы(матрица)\]

Екінші жолға назар аударыңыз: бөлгіш қазірдің өзінде ортақ болған кезде, яғни. үш бөлек бөлшектің орнына бір үлкенін жаздық, жақшадан бірден құтылмау керек. Қосымша жолды жазып, айталық, үшінші бөлшекке дейін минус болғанын ескерген дұрыс - және ол ешқайда кетпейді, бірақ жақшаның алдындағы нумераторда «ілулі болады». Бұл сізді көптеген қателіктерден сақтайды.

Ал, соңғы жолда алымды көбейткіштерге бөлу пайдалы. Сонымен қатар, бұл дәл квадрат және қысқартылған көбейту формулалары бізге қайтадан көмектеседі. Бізде бар:

\[\frac(((x)^(2))-4x+4)(\left(x-2 \right)\left(((x)^(2))+2x+4 \оң))= \frac(((\сол(x-2 \оң))^(2)))(\сол(x-2 \оң)\сол(((x)^(2))+2x+4 \оң) )=\frac(x-2)((x)^(2))+2x+4)\]

Енді екінші жақшамен де дәл осылай айналысайық. Мұнда мен жай ғана теңдіктер тізбегін жазамын:

\[\бастау(матрица) \frac(((x)^(2)(((x)^(2))-4)-\frac(2)(2-x)=\frac((( x)^(2))))(\сол(x-2 \оң)\сол(x+2 \оң))-\frac(2)(2-x)= \\ =\frac(((x)) ^(2)(\сол(x-2 \оң)\сол(x+2 \оң))+\frac(2)(x-2)= \\ =\frac((x)^( 2)))(\сол(x-2 \оң)\сол(x+2 \оң))+\frac(2\cdot \left(x+2 \оң))(\сол(x-2 \оң) )\cdot \left(x+2 \right))= \\ =\frac(((x)^(2))+2\cdot \left(x+2 \right))(\left(x-2) \right)\left(x+2 \right))=\frac(((x)^(2))+2x+4)(\left(x-2 \оң)\сол(x+2 \оң) ). \\ \соңы(матрица)\]

Біз бастапқы мәселеге ораламыз және өнімді қараймыз:

\[\frac(x-2)((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2) \right)\left(x+2 \right))=\frac(1)(x+2)\]

Жауабы: \[\frac(1)(x+2)\].

Бұл есептің мәні алдыңғы есеппен бірдей: егер сіз оларды түрлендіруге ақылмен жақындасаңыз, рационалды өрнектерді қаншалықты жеңілдетуге болатынын көрсету.

Ал енді осының барлығын білген соң бүгінгі сабағымыздың негізгі тақырыбы – бөлшек рационал теңсіздіктерді шешуге көшейік. Оның үстіне, мұндай дайындықтан кейін теңсіздіктердің өзі жаңғақ сияқты болады. :)

Рационал теңсіздіктерді шешудің негізгі жолы

Рационал теңсіздіктерді шешудің кем дегенде екі тәсілі бар. Енді біз олардың бірін қарастырамыз - мектеп математика курсында жалпы қабылданған.

Бірақ алдымен маңызды детальға назар аударайық. Барлық теңсіздіктер екі түрге бөлінеді:

1. Қатаң: $f\left(x \right) \gt 0$ немесе $f\left(x \right) \lt 0$;
2. Қатаң емес: $f\left(x \right)\ge 0$ немесе $f\left(x \right)\le 0$.

Екінші типтегі теңсіздіктер біріншіге оңай келтіріледі, сонымен қатар теңдеу:

Бұл шағын «қосымша» $f\left(x \right)=0$ толтырылған нүктелер сияқты жағымсыз нәрсеге әкеледі - біз оларды интервалдық әдісте кездестірдік. Әйтпесе, қатаң және қатаң емес теңсіздіктер арасында ешқандай айырмашылық жоқ, сондықтан әмбебап алгоритмді талдап көрейік:

1. Барлық нөл емес элементтерді теңсіздік белгісінің бір жағына жинаңыз. Мысалы, сол жақта;
2. Барлық бөлшектерді ортақ бөлгішке келтіріңіз (егер мұндай бөлшек бірнеше болса), ұқсас бөлшектерді келтіріңіз. Содан кейін, мүмкін болса, алым мен бөлгішті көбейткіштерге бөліңіз. Қалай болғанда да, $\frac(P\left(x \right))(Q\left(x \right))\vee 0$ түріндегі теңсіздікті аламыз, мұндағы құсбелгі теңсіздік белгісі.
3. Алымды нөлге теңестіріңіз: $P\left(x \right)=0$. Бұл теңдеуді шешеміз және түбірлерді аламыз $((x)_(1))$, $((x)_(2))$, $((x)_(3))$, ... Содан кейін біз талап етеміз. бөлгіш нөлге тең болмағаны: $Q\left(x \right)\ne 0$. Әрине, мәні бойынша $Q\left(x \right)=0$ теңдеуін шешуіміз керек және $x_(1)^(*)$, $x_(2)^(*) түбірлерін аламыз. $, $x_(3 )^(*)$, ... (нақты есептерде мұндай түбір үштен көп болмайды).
4. Осы түбірлердің барлығын (жұлдызшасы бар және жұлдызсыз) бір сан сызығына белгілейміз, ал жұлдызсыз түбірлерді бояймыз, ал жұлдызшалары бар түбірлерді тесеміз.
5. Біз плюс және минус таңбаларын қоямыз, бізге қажет аралықтарды таңдаймыз. Егер теңсіздіктің $f\left(x \right) \gt 0$ пішіні болса, онда жауап "плюс" белгісімен белгіленген интервалдар болады. $f\left(x \right) \lt 0$ болса, онда "минустары" бар аралықтарды қарастырамыз.

Тәжірибе көрсеткендей, 2 және 4-тармақтар ең үлкен қиындықтарды тудырады - сауатты түрлендірулер және өсу ретімен сандарды дұрыс орналастыру. Ал, соңғы қадамда өте сақ болыңыз: біз әрқашан белгілерді негізге аламыз теңдеулерге көшу алдында жазылған соңғы теңсіздік. Бұл интервал әдісінен мұраланған әмбебап ереже.

Демек, схема бар. Жаттығу жасайық.

Тапсырма. Теңсіздікті шеш:

\[\frac(x-3)(x+7) \lt 0\]

Шешім. Бізде $f\left(x \right) \lt 0$ түріндегі қатаң теңсіздік бар. Әлбетте, біздің схеманың 1 және 2 тармақтары қазірдің өзінде аяқталды: теңсіздіктің барлық элементтері сол жақта жиналады, ештеңені ортақ бөлгішке келтірудің қажеті жоқ. Ендеше үшінші тармаққа көшейік.

Санды нөлге қойыңыз:

\[\бастау(туралау) & x-3=0; \\ &x=3. \соңы(туралау)\]

Ал бөлгіш:

\[\бастау(туралау) & x+7=0; \\ & ((x)^(*))=-7. \\ \соңы(туралау)\]

Бұл жерде көптеген адамдар кептеліп қалады, өйткені теорияда ODZ талап еткендей $x+7\ne 0$ жазу керек (сіз нөлге бөлуге болмайды, бұл бәрі). Ақыр соңында, біз болашақта бөлгіштен шыққан нүктелерді шығарамыз, сондықтан сіз өз есептеулеріңізді қайтадан қиындатпауыңыз керек - барлық жерде тең белгіні жазыңыз және алаңдамаңыз. Бұл үшін ешкім ұпай шегермейді. :)

Төртінші нүкте. Алынған түбірлерді сандар жолында белгілейміз:

Барлық нүктелер тесілген, өйткені теңсіздік қатаң

Назар аударыңыз: бастапқы теңсіздік қатаң болғандықтан барлық нүктелер тесілген. Енді бұл маңызды емес: бұл нүктелер алымнан немесе бөлгіштен келді.

Ал, белгілерге қараңыз. Кез келген $((x)_(0)) \gt 3$ санын алыңыз. Мысалы, $((x)_(0))=100$ (бірақ сіз $((x)_(0))=3,1$ немесе $((x)_(0)) = алуыңыз мүмкін еді. 1\000\000$). Біз алып жатырмыз:

Сонымен, барлық тамырлардың оң жағында бізде оң аймақ бар. Және әрбір түбір арқылы өткенде белгі өзгереді (бұл әрқашан болмайды, бірақ кейінірек бұл туралы толығырақ). Сондықтан біз бесінші тармаққа көшеміз: біз белгілерді қойып, дұрысын таңдаймыз:

Біз теңдеулерді шешуге дейінгі соңғы теңсіздікке ораламыз. Шындығында, бұл түпнұсқамен сәйкес келеді, өйткені біз бұл тапсырмада ешқандай түрлендірулер жасамадық.

$f\left(x \right) \lt 0$ түріндегі теңсіздікті шешу қажет болғандықтан, мен $x\ интервалын \left(-7;3 \right)$-ға көлеңкеледім - бұл жалғыз. минус белгісімен белгіленеді. Бұл жауап.

Жауабы: $x\in \left(-7;3 \right)$

Осымен болды! Бұл қиын ба? Жоқ, қиын емес. Расында, бұл оңай жұмыс болды. Енді миссияны сәл қиындатып, «сәнді» теңсіздікті қарастырайық. Оны шешкен кезде мен бұдан былай мұндай егжей-тегжейлі есептеулерді бермеймін - мен жай ғана негізгі ойларды сипаттаймын. Жалпы, біз оны тәуелсіз жұмыста немесе емтиханда жасағандай реттейміз. :)

Тапсырма. Теңсіздікті шеш:

\[\frac(\left(7x+1 \оң)\сол(11x+2 \оң))(13x-4)\ge 0\]

Шешім. Бұл $f\left(x \right)\ge 0$ түріндегі қатаң емес теңсіздік. Барлық нөлдік емес элементтер сол жақта жиналады, әртүрлі бөлгіштер жоқ. Теңдеулерге көшейік.

Сан:

\[\бастау(туралау) & \left(7x+1 \оңға)\left(11x+2 \оңға)=0 \\ & 7x+1=0\Оң жақ көрсеткі ((x)_(1))=-\ frac(1)(7); \\ & 11x+2=0\Оң жақ көрсеткі ((x)_(2))=-\frac(2)(11). \\ \соңы(туралау)\]

Бөлгіш:

\[\бастау(туралау) & 13x-4=0; \\ & 13x=4; \\ & ((x)^(*))=\frac(4)(13). \\ \соңы(туралау)\]

Мен бұл мәселені қандай бұрмалаушылық жасағанын білмеймін, бірақ түбірлер жақсы нәтиже бермеді: оларды сандар сызығында орналастыру қиын болады. Ал $((x)^(*))=(4)/(13)\;$ түбірімен бәрі азды-көпті анық болса (бұл жалғыз оң сан – оң жақта болады), онда $ ((x)_(1 ))=-(1)/(7)\;$ және $((x)_(2))=-(2)/(11)\;$ қосымша зерттеуді қажет етеді: қайсысы үлкенірек?

Сіз мұны біле аласыз, мысалы:

\[((x)_(1))=-\frac(1)(7)=-\frac(2)(14) \gt -\frac(2)(11)=((x)_(2) ))\]

Сандық бөлшек $-(2)/(14)\; \gt -(2)/(11)\;$? Қажет болса, бөлшектермен әрекеттерді қалай орындау керектігін есте сақтауды ұсынамын.

Ал біз барлық үш түбірді сандар жолында белгілейміз:

Алымдағы нүктелер көлеңкеленеді, ал бөлгіштен олар қиылады

Біз белгілер қоямыз. Мысалы, сіз $((x)_(0))=1$ алып, осы нүктедегі белгіні таба аласыз:

\[\бастау(туралау) & f\left(x \right)=\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4); \\ & f\left(1 \right)=\frac(\left(7\cdot 1+1 \right)\left(11\cdot 1+2 \right))(13\cdot 1-4)=\ frac(8\cdot 13)(9) \gt 0. \\\соңы(туралау)\]

Теңдеулердің алдындағы соңғы теңсіздік $f\left(x \right)\ge 0$ болды, сондықтан бізді қосу таңбасы қызықтырады.

Біз екі жиын алдық: бірі кәдімгі кесінді, екіншісі - сан түзуіндегі ашық сәуле.

Жауабы: $x\in \left[ -\frac(2)(11);-\frac(1)(7) \right]\bigcup \left(\frac(4)(13);+\infty \right )$

Ең оң жақ интервалдағы белгіні табу үшін біз ауыстыратын сандар туралы маңызды ескерту. Ең оң жақ түбірге жақын санды ауыстыру қажет емес. Сіз миллиардтарды немесе тіпті «плюс-шексіздікті» ала аласыз - бұл жағдайда жақшадағы, алымдағы немесе бөлгіштегі көпмүшенің таңбасы тек жетекші коэффициенттің белгісімен анықталады.

Соңғы теңсіздіктен $f\left(x \right)$ функциясын тағы бір қарастырайық:

Ол үш көпмүшені қамтиды:

\[\бастау(туралау) & ((P)_(1))\left(x \right)=7x+1; \\ & ((P)_(2))\left(x \right)=11x+2; \\ & Q\сол(x\оң)=13x-4. \соңы(туралау)\]

Олардың барлығы сызықтық биномдар және олардың барлығының оң коэффициенттері бар (7, 11 және 13 сандары). Сондықтан, өте үлкен сандарды ауыстырған кезде, көпмүшелердің өздері де оң болады. :)

Бұл ереже тым күрделі болып көрінуі мүмкін, бірақ біз өте оңай тапсырмаларды талдағанда ғана. Күрделі теңсіздіктерде «плюс-шексіздік» ауыстыру $((x)_(0))=100$ стандартынан әлдеқайда жылдамырақ белгілерді анықтауға мүмкіндік береді.

Біз жақын арада осындай қиындықтарға тап боламыз. Бірақ алдымен бөлшек рационал теңсіздіктерді шешудің баламалы әдісін қарастырайық.

Альтернативті жол

Бұл әдісті маған бір шәкіртім ұсынған. Мен өзім оны ешқашан пайдаланған емеспін, бірақ тәжірибе көрсеткендей, көптеген оқушылар үшін теңсіздіктерді осылай шешу шынымен ыңғайлырақ.

Демек, бастапқы деректер бірдей. Бөлшек рационал теңсіздікті шешу керек:

\[\frac(P\left(x \оң))(Q\сол(x \оң)) \gt 0\]

Ойланып көрейік: неге $Q\left(x \right)$ көпмүшесі $P\left(x \right)$ көпмүшесінен "нашар"? Неліктен біз түбірлердің бөлек топтарын (жұлдызшамен және жұлдызсыз) қарастыруымыз керек, тесілген нүктелер туралы ойлауымыз керек және т.б.? Қарапайым: бөлшектің анықтау облысы бар, оған сәйкес бөлшек оның бөлгіші нөлден өзгеше болғанда ғана мағыналы болады.

Әйтпесе, алым мен бөлгіштің айырмашылығы жоқ: біз де оны нөлге теңестіреміз, түбірлерді іздейміз, содан кейін оларды сандық сызыққа белгілейміз. Ендеше, неге бөлшек жолағын (шын мәнінде бөлу белгісін) кәдімгі көбейтумен алмастырмасқа, ал ДСЖ-ның барлық талаптарын жеке теңсіздік ретінде жазуға болмайды? Мысалы, келесідей:

\[\frac(P\left(x \оң))(Q\сол(x \оң)) \gt 0\Оң жақ көрсеткі \сол\( \бастау(туралау) & P\left(x \оң)\cdot Q \left(x \right) \gt 0, \\ & Q\left(x \right)\ne 0. \\ \соңы(туралау) \оңға.\]

Назар аударыңыз: бұл тәсіл мәселені интервалдар әдісіне дейін азайтуға мүмкіндік береді, бірақ бұл шешімді мүлде қиындатпайды. Ақыр соңында, біз $Q\left(x \right)$ көпмүшені нөлге теңестіреміз.

Оның нақты тапсырмаларда қалай жұмыс істейтінін көрейік.

Тапсырма. Теңсіздікті шеш:

\[\frac(x+8)(x-11) \gt 0\]

Шешім. Сонымен, интервал әдісіне көшейік:

\[\frac(x+8)(x-11) \gt 0\Оң жақ көрсеткі \сол\( \бастау(туралау) & \left(x+8 \оң)\сол(x-11 \оң) \gt 0 , \\ & x-11\ne 0. \\ \соңы(туралау) \оңға.\]

Бірінші теңсіздік элементар түрде шешіледі. Әрбір жақшаны нөлге қойыңыз:

\[\бастау(туралау) & x+8=0\Оң жақ көрсеткі ((x)_(1))=-8; \\ & x-11=0\Оң жақ көрсеткі ((x)_(2))=11. \\ \соңы(туралау)\]

Екінші теңсіздікпен бәрі де қарапайым:

Нақты түзуде $((x)_(1))$ және $((x)_(2))$ нүктелерін белгілейміз. Олардың барлығы тесілген, өйткені теңсіздік қатаң:

Оң жақ жері екі рет тесілген болып шықты. Бұл жақсы.

$x=11$ нүктесіне назар аударыңыз. Оны «екі рет ойып алған» болып шықты: бір жағынан, біз оны теңсіздіктің ауырлығынан, екінші жағынан, ОДЗ-ның қосымша талабына байланысты ойып тастаймыз.

Қалай болғанда да, бұл жай ғана тесілген нүкте болады. Сондықтан біз $\left(x+8 \right)\left(x-11 \right) \gt 0$ теңсіздігінің белгілерін қойдық - біз теңдеулерді шешуді бастамас бұрын көрген соңғысы:

Бізді оң аймақтар қызықтырады, өйткені біз $f\left(x \right) \gt 0$ түріндегі теңсіздікті шешіп жатырмыз және біз оларды бояймыз. Жауабын жазу ғана қалды.

Жауап. $x\in \left(-\infty;-8 \right)\bigcup \left(11;+\infty \right)$

Осы шешімді мысал ретінде қолдана отырып, мен сізді жаңадан бастаған студенттер арасында жиі кездесетін қателіктен сақтандырғым келеді. Атап айтқанда: теңсіздіктерде ешқашан жақша ашпаңыз! Керісінше, бәрін факторлауға тырысыңыз - бұл шешімді жеңілдетеді және сізді көптеген мәселелерден құтқарады.

Енді қиынырақ нәрсені көрейік.

Тапсырма. Теңсіздікті шеш:

\[\frac(\left(2x-13 \right)\left(12x-9 \right))(15x+33)\le 0\]

Шешім. Бұл $f\left(x \right)\le 0$ пішінінің қатаң емес теңсіздігі, сондықтан мұнда толтырылған нүктелерді мұқият бақылау керек.

Интервал әдісіне көшейік:

\[\left\( \бастау(туралау) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \оң)\le 0, \\ & 15x+33\ ne 0. \\ \соңы(туралау) \оңға.\]

Теңдеуге көшейік:

\[\бастау(туралау) & \left(2x-13 \оң)\left(12x-9 \оң)\left(15x+33 \оң)=0 \\ & 2x-13=0\Оң жақ көрсеткі ((x) )_(1))=6,5; \\ & 12x-9=0\Оң жақ көрсеткі ((x)_(2))=0,75; \\ & 15x+33=0\Оң жақ көрсеткі ((x)_(3))=-2,2. \\ \соңы(туралау)\]

Біз қосымша талапты ескереміз:

Барлық алынған түбірлерді сандар жолында белгілейміз:

Егер нүкте бір уақытта тесіліп, толтырылса, ол тесілген болып саналады.

Тағы да екі нүкте бір-бірімен «қабатталады» - бұл қалыпты жағдай, әрқашан солай болады. Тек тесілген және толтырылған деп белгіленген нүкте шын мәнінде тесілген нүкте екенін түсіну маңызды. Анау. «Боялу» - «бояуға» қарағанда күштірек әрекет.

Бұл мүлдем қисынды, өйткені тесу арқылы біз функцияның белгісіне әсер ететін нүктелерді белгілейміз, бірақ олар жауапқа қатыспайды. Ал егер бір сәтте сан бізге сәйкес келмей қалса (мысалы, ол ODZ-ге түспесе), біз оны тапсырманың соңына дейін қараудан алып тастаймыз.

Жалпы, философияны доғарыңыз. Біз белгілерді реттеп, минус белгісімен белгіленген аралықтарды бояймыз:

Жауап. $x\in \left(-\infty ;-2,2 \right)\bigcup \left[ 0,75;6,5 \right]$.

Мен тағы да мына теңдеуге назарларыңызды аударғым келді:

\[\сол(2х-13 \оң)\сол(12х-9 \оң)\сол(15х+33 \оң)=0\]

Тағы да: мұндай теңдеулерде ешқашан жақша ашпаңыз! Сіз мұны тек өзіңізге қиындатасыз. Есіңізде болсын: факторлардың кем дегенде біреуі нөлге тең болғанда өнім нөлге тең болады. Демек, бұл теңдеу біз алдыңғы есепте шешкен бірнеше кішігірім теңдеулерге «бөлінеді».

Тамырлардың көптігін ескеру

Алдыңғы есептерден дәл қатаң емес теңсіздіктер ең қиын екенін байқау қиын емес, өйткені оларда толтырылған нүктелерді қадағалау керек.

Бірақ әлемде одан да үлкен зұлымдық бар - бұл теңсіздіктердің көптеген тамырлары. Мұнда кейбір толтырылған нүктелерді ұстану қажет емес - мұнда теңсіздік белгісі дәл осы нүктелерден өткенде кенеттен өзгермеуі мүмкін.

Біз бұл сабақта мұндай ештеңені әлі қарастырған жоқпыз (бірақ интервал әдісінде ұқсас мәселе жиі кездесті). Сонымен, жаңа анықтаманы енгізейік:

Анықтама. $((\left(x-a \right))^(n))=0$ теңдеуінің түбірі $x=a$-ға тең және $n$-шы көбейтіндінің түбірі деп аталады.

Шын мәнінде, біз көптің нақты мәніне ерекше қызығушылық танытпаймыз. Жалғыз маңызды нәрсе - бұл $n$ саны жұп немесе тақ. Өйткені:

1. Егер $x=a$ жұп еселік түбірі болса, онда функцияның таңбасы ол арқылы өткенде өзгермейді;
2. Және керісінше, егер $x=a$ тақ көбейтіндінің түбірі болса, онда функцияның таңбасы өзгереді.

Тақ көбейтіндінің түбірінің ерекше жағдайы осы сабақта қарастырылған алдыңғы есептердің барлығы болып табылады: онда көптік барлық жерде бірге тең.

Және одан әрі. Мәселелерді шешуді бастамас бұрын, мен тәжірибелі студентке түсінікті болып көрінетін, бірақ көптеген жаңадан бастағандарды ессіз қалдыратын бір нәзік нәрсеге назар аударғым келеді. Атап айтқанда:

$n$ көптік түбірі бүкіл өрнек осы дәрежеге көтерілгенде ғана пайда болады: $((\left(x-a \right))^(n))$, $\left(((x)^( n) емес )-a\right)$.

Тағы да: $((\left(x-a \right))^(n))$ жақшасы $n$ көптігінің $x=a$ түбірін береді, бірақ $\left(((x)^() жақшасы n)) -a \right)$ немесе жиі болатындай, $(a-((x)^(n)))$ бізге бірінші еселіктің түбірін (немесе екі түбір, егер $n$ жұп болса) береді , $n$ не тең болса да.

Салыстыру:

\[((\сол(x-3 \оң))^(5))=0\Оң жақ көрсеткі x=3\сол(5к \оң)\]

Мұнда бәрі түсінікті: бүкіл кронштейн бесінші қуатқа көтерілді, сондықтан шығу кезінде біз бесінші дәреженің түбірін алдық. Ал енді:

\[\left(((x)^(2))-4 \right)=0\Оң жақ көрсеткі ((x)^(2))=4\Оң жақ көрсеткі x=\pm 2\]

Бізде екі түбір бар, бірақ екеуінің де бірінші еселігі бар. Немесе тағы біреуі:

\[\left(((x)^(10))-1024 \right)=0\Оң жақ көрсеткі ((x)^(10))=1024\Оң жақ көрсеткі x=\pm 2\]

Және оныншы дәрежеде шатастырмаңыз. Ең бастысы, 10 - жұп сан, сондықтан шығыста екі түбір бар және олардың екеуінде қайтадан бірінші еселік болады.

Жалпы, абай болыңыз: көптік тек қашан болады дәреже тек айнымалыға емес, бүкіл жақшаға қолданылады.

Тапсырма. Теңсіздікті шеш:

\[\frac(((x)^(2))((\сол(6-x \оң))^(3))\left(x+4 \оң))(((\сол(x+7) \оң))^(5)))\ge 0\]

Шешім. Оны балама жолмен шешуге тырысайық - жекеден өнімге көшу арқылы:

\[\left\( \begin(туралау) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ( (\left(x+7 \right))^(5))\ge 0, \\ & ((\left(x+7 \right))^(5))\ne 0. \\ \соңы(туралау) )\оң.\]

Бірінші теңсіздікті интервал әдісімен қарастырамыз:

\[\бастау(туралау) & ((x)^(2))((\left(6-x \оң))^(3))\left(x+4 \оң)\cdot ((\left() x+7 \right))^(5))=0; \\ & ((x)^(2))=0\Оң жақ көрсеткі x=0\сол(2k \оң); \\ & ((\сол(6-x \оң))^(3))=0\Оң жақ көрсеткі x=6\сол(3k \оң); \\ & x+4=0\Оң жақ көрсеткі x=-4; \\ & ((\сол(x+7 \оң))^(5))=0\Оң жақ көрсеткі x=-7\сол(5k \оң). \\ \соңы(туралау)\]

Қосымша екінші теңсіздікті шешеміз. Шындығында, біз оны шештік, бірақ рецензенттер шешімнен мін таппауы үшін оны қайтадан шешкен дұрыс:

\[((\сол(x+7 \оң))^(5))\ne 0\Оң жақ көрсеткі x\ne -7\]

Соңғы теңсіздікте көбейткіштер жоқ екенін ескеріңіз. Шынында да: сандар түзуіндегі $x=-7$ нүктесін неше рет сызып тастаудың айырмашылығы қандай? Кем дегенде бір рет, кем дегенде бес рет - нәтиже бірдей болады: тесілген нүкте.

Сан сызығында алған барлық нәрсені атап өтейік:

Мен айтқанымдай, $x=-7$ нүктесі ақырында жойылады. Көбейтінділер теңсіздікті интервал әдісімен шешу негізінде орналасады.

Белгілерді қою қалды:

$x=0$ нүктесі жұп көбейтіндінің түбірі болғандықтан, ол арқылы өткенде таңбасы өзгермейді. Қалған нүктелердің тақ көптігі бар және олармен бәрі қарапайым.

Жауап. $x\in \left(-\infty ;-7 \right)\bigcup \left[ -4;6 \right]$

$x=0$ мәніне қайта назар аударыңыз. Біркелкі көптігінің арқасында қызықты әсер пайда болады: оның сол жағындағы барлық нәрсе боялған, оң жағында - сонымен қатар, нүктенің өзі толығымен боялған.

Нәтижесінде жауапты жазу кезінде оны оқшаулау қажет емес. Анау. $x\in \left[ -4;0 \right]\bigcup \left[ 0;6 \right]$ сияқты нәрсені жазудың қажеті жоқ (бірақ ресми түрде мұндай жауап дұрыс болар еді). Оның орнына \left[ -4;6 \right]$ ішіне $x\ деп бірден жазамыз.

Мұндай әсерлер тек жұп сандық түбірлер үшін ғана мүмкін. Ал келесі тапсырмада біз бұл әсердің кері «көрінісін» кездестіреміз. Дайын ба?

Тапсырма. Теңсіздікті шеш:

\[\frac(((\left(x-3 \оң))^(4))\left(x-4 \оң))(((\left(x-1 \оң))^(2)) \left(7x-10-((x)^(2)) \right))\ge 0\]

Шешім. Бұл жолы біз стандартты схеманы ұстанамыз. Санды нөлге қойыңыз:

\[\бастау(туралау) & ((\сол(x-3 \оңға))^(4))\left(x-4 \оңға)=0; \\ & ((\сол(x-3 \оң))^(4))=0\Оң жақ көрсеткі ((x)_(1))=3\сол(4k \оң); \\ & x-4=0\Оң жақ көрсеткі ((x)_(2))=4. \\ \соңы(туралау)\]

Ал бөлгіш:

\[\бастау(туралау) & ((\left(x-1 \оңға))^(2))\left(7x-10-((x)^(2)) \оңға)=0; \\ & ((\сол(x-1 \оң))^(2))=0\Оң жақ көрсеткі x_(1)^(*)=1\сол(2k \оң); \\ & 7x-10-((x)^(2))=0\Оң жақ көрсеткі x_(2)^(*)=5;\ x_(3)^(*)=2. \\ \соңы(туралау)\]

Біз $f\left(x \right)\ge 0$ түріндегі қатаң емес теңсіздікті шешіп жатқандықтан, бөлгіштің түбірлері (жұлдызшалары бар) қиылады, ал алымдағылары боялады. .

Біз белгілерді реттейміз және «плюс» белгісімен белгіленген аймақтарды сызамыз:

$x=3$ нүктесі оқшауланған. Бұл жауаптың бөлігі

Соңғы жауапты жазбас бұрын, суретке мұқият қараңыз:

1. $x=1$ нүктесінің жұп көптігі бар, бірақ өзі тесілген. Сондықтан жауапта оны оқшаулау керек болады: $x\in емес, \left(-\infty ;1 \right)\bigcup \left(1;2 \right)$ деп $x\ деп жазу керек. \left(-\ infty ;2\right)$.
2. $x=3$ нүктесі де жұп көбейтіндіге ие және көлеңкеленген. Белгілердің орналасуы нүктенің өзі бізге сәйкес келетінін көрсетеді, бірақ солға және оңға қадам - ​​және біз өзімізді сөзсіз бізге сәйкес келмейтін аймақта табамыз. Мұндай нүктелер оқшауланған деп аталады және $x\in \left\( 3 \right\)$ түрінде жазылады.

Біз барлық алынған бөліктерді ортақ жиынтыққа біріктіріп, жауапты жазамыз.

Жауабы: $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;5 \right) $

Анықтама. Теңсіздікті шешу дегеніміз оның барлық шешімдерінің жиынын табыңыз, немесе бұл жиынның бос екенін дәлелдеңіз.

Көрінетін сияқты: бұл жерде не түсініксіз болуы мүмкін? Иә, мәселенің мәні мынада, жиынтықтарды әртүрлі тәсілдермен көрсетуге болады. Соңғы есептің жауабын қайта жазайық:

Жазылғанын сөзбе-сөз оқимыз. «Х» айнымалысы төрт бөлек жиынның бірігуімен («U» символы) алынатын белгілі бір жиынға жатады:

• $\left(-\infty ;1 \right)$ аралығы, ол сөзбе-сөз "бірден кіші барлық сандар, бірақ бір өзі емес" дегенді білдіреді;
• Аралық $\left(1;2 \right)$, яғни. «1 мен 2 арасындағы барлық сандар, бірақ 1 және 2 сандарының өздері емес»;
• $\left\( 3 \right\)$ жиыны, бір саннан тұратын - үш;
• $\left[ 4;5 \right)$ аралығы 4-тен 5-ке дейінгі барлық сандарды және 4-тің өзін қамтиды, бірақ 5 емес.

Бұл жерде үшінші мәселе қызықтырады. Сандардың шексіз жиынын анықтайтын және тек осы жиындардың шекарасын ғана белгілейтін интервалдардан айырмашылығы, $\left\( 3 \right\)$ жиыны санау арқылы дәл бір санды анықтайды.

Жиынға енгізілген нақты сандарды (және шекараларды немесе басқа ештеңені белгілемей) тізімдеп жатқанымызды түсіну үшін бұйра жақшалар қолданылады. Мысалы, $\left\( 1;2 \right\)$ белгісі дәл "екі саннан тұратын жиынды: 1 және 2" дегенді білдіреді, бірақ 1-ден 2-ге дейінгі сегмент емес. Ешбір жағдайда бұл ұғымдарды шатастырмаңыз. .

Көптікті қосу ережесі

Ал, бүгінгі сабақтың соңында Павел Бердовтан кішкене қалайы. :)

Зейінді оқушылар өздеріне сұрақ қойған шығар: алым мен бөлгіште бірдей түбірлер табылса не болады? Сонымен, келесі ереже жұмыс істейді:

Бірдей түбірлердің көптігі қосылады. Әрқашан. Бұл түбір алымда да, бөлімде де кездессе де.

Кейде сөйлескеннен гөрі шешім қабылдаған дұрыс. Сондықтан біз келесі мәселені шешеміз:

Тапсырма. Теңсіздікті шеш:

\[\frac(((x)^(2))+6x+8)(\left(((x)^(2))-16 \right)\left(((x)^(2))+ 9x+14 \оңға))\ge 0\]

\[\бастау(туралау) & ((x)^(2))+6x+8=0 \\ & ((x)_(1))=-2;\ ((x)_(2))= -4. \\ \соңы(туралау)\]

Әзірге ерекше ештеңе жоқ. Бөлгішті нөлге қойыңыз:

\[\бастау(туралау) & \left(((x)^(2))-16 \right)\left((x)^(2))+9x+14 \оңға)=0 \\ & ( (x)^(2))-16=0\Оң жақ көрсеткі x_(1)^(*)=4;\ x_(2)^(*)=-4; \\ & ((x)^(2))+9x+14=0\Оң жақ көрсеткі x_(3)^(*)=-7;\ x_(4)^(*)=-2. \\ \соңы(туралау)\]

Екі бірдей түбір табылды: $((x)_(1))=-2$ және $x_(4)^(*)=-2$. Екеуінің де бірінші еселігі бар. Сондықтан оларды бір түбірмен ауыстырамыз $x_(4)^(*)=-2$, бірақ еселігі 1+1=2.

Сонымен қатар, бірдей түбірлер де бар: $((x)_(2))=-4$ және $x_(2)^(*)=-4$. Олар да бірінші еселік болып табылады, сондықтан 1+1=2 еселігінің $x_(2)^(*)=-4$ ғана қалады.

Назар аударыңыз: екі жағдайда да біз дәл «кесілген» түбірді қалдырдық, ал «боялғанын» қараудан тастадық. Өйткені сабақтың басында да біз келістік: егер нүкте бір уақытта тесіліп, боялған болса, біз оны бәрібір тесілген деп есептейміз.

Нәтижесінде бізде төрт тамыр бар және олардың барлығы ойылып шықты:

\[\бастау(туралау) & x_(1)^(*)=4; \\ & x_(2)^(*)=-4\left(2k \оң); \\ & x_(3)^(*)=-7; \\ & x_(4)^(*)=-2\сол(2k \оң). \\ \соңы(туралау)\]

Біз оларды көбейтіндіні ескере отырып, сандар жолында белгілейміз:

Біз белгілерді орналастырып, бізді қызықтыратын жерлерге бояймыз:

Барлығы. Оқшауланған нүктелер мен басқа да бұрмаланулар жоқ. Жауабын жазуға болады.

Жауап. $x\in \left(-\infty ;-7 \right)\bigcup \left(4;+\infty \right)$.

көбейту ережесі

Кейде одан да жағымсыз жағдай орын алады: бірнеше түбірі бар теңдеудің өзі белгілі бір қуатқа көтеріледі. Бұл барлық бастапқы түбірлердің көптігін өзгертеді.

Бұл сирек кездеседі, сондықтан студенттердің көпшілігінің мұндай есептерді шешу тәжірибесі жоқ. Ал мұндағы ереже:

Теңдеуді $n$ дәрежесіне көтергенде, оның барлық түбірлерінің еселігі де $n$ есе артады.

Басқаша айтқанда, дәрежеге көтеру көбейтінділерді бірдей дәрежеге көбейтуге әкеледі. Мысал ретінде осы ережені алайық:

Тапсырма. Теңсіздікті шеш:

\[\frac(x((\left(((x)^(2))-6x+9 \оң))^(2))((\left(x-4 \оң))^(5)) )(((\left(2-x \оң))^(3))((\left(x-1 \оң))^(2)))\le 0\]

Шешім. Санды нөлге қойыңыз:

Көбейткіштердің ең болмағанда біреуі нөлге тең болғанда туынды нөлге тең болады. Бірінші көбейткішпен бәрі түсінікті: $x=0$. Міне, проблемалар осы жерден басталады:

\[\бастау(туралау) & ((\left(((x)^(2))-6x+9 \оң))^(2))=0; \\ & ((x)^(2))-6x+9=0\left(2k \оң); \\ & D=((6)^(3))-4\cdot 9=0 \\ & ((x)_(2))=3\left(2k \оң)\сол(2к \оң) \ \ & ((x)_(2))=3\сол(4k \оң) \\ \соңы(туралау)\]

Көріп отырғаныңыздай, $((x)^(2))-6x+9=0$ теңдеуінің екінші еселігінің бірегей түбірі бар: $x=3$. Содан кейін барлық теңдеу квадратқа алынады. Демек, түбірдің еселігі $2\cdot 2=4$ болады, оны біз соңында жазып алдық.

\[((\сол(x-4 \оң))^(5))=0\Оң жақ көрсеткі x=4\сол(5к \оң)\]

Бөлгіште де проблема жоқ:

\[\бастау(туралау) & ((\left(2-x \right))^(3))((\left(x-1 \right))^(2))=0; \\ & ((\left(2-x \оң))^(3))=0\Оң жақ көрсеткі x_(1)^(*)=2\left(3k \оң); \\ & ((\сол(x-1 \оң))^(2))=0\Оң жақ көрсеткі x_(2)^(*)=1\сол(2k \оң). \\ \соңы(туралау)\]

Барлығы бес ұпай алдық: екеуі жұдырықтасты, үшеуі толтырылды. Алым мен бөлгіште сәйкес келетін түбірлер жоқ, сондықтан біз оларды сандар түзуінде белгілейміз:

Біз белгілерді көбейтуді ескере отырып реттейміз және бізді қызықтыратын аралықтарды бояймыз:

Тағы бір оқшауланған нүкте және бір тесілген

Біркелкі көптіктің тамырына байланысты біз қайтадан бірнеше «стандартты емес» элементтерді алдық. Бұл $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)$, $x\in \left[ 0;2 \right)$ емес, сонымен қатар $ оқшауланған нүкте. x\in \left\( 3 \right\)$.

Жауап. $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;+\infty \right)$

Көріп отырғаныңыздай, бәрі соншалықты қиын емес. Ең бастысы - мұқият болу. Бұл сабақтың соңғы бөлімі трансформацияларға арналған - біз басында талқылағандар.

Алдын ала түрлендірулер

Бұл бөлімде қарастыратын теңсіздіктер күрделі емес. Дегенмен, алдыңғы тапсырмалардан айырмашылығы, мұнда рационал бөлшектер теориясынан - көбейткіштерге бөлу және ортақ бөлгішке келтіру дағдыларын қолдануға тура келеді.

Біз бүгінгі сабақтың басында бұл мәселені жан-жақты талқыладық. Егер сіз оның не туралы екенін түсінгеніңізге сенімді болмасаңыз, мен сізге оралып, қайталауды ұсынамын. Өйткені бөлшектерді түрлендіруде «жүзіп» жүрсеңіз, теңсіздіктерді шешудің әдістерін тым көп тоқудың қажеті жоқ.

Айтпақшы, үй тапсырмаларында да ұқсас тапсырмалар көп болады. Олар бөлек бөлімге орналастырылған. Онда сіз өте маңызды емес мысалдарды таба аласыз. Бірақ бұл үй тапсырмасында болады, бірақ енді осындай бір-екі теңсіздікті талдап көрейік.

Тапсырма. Теңсіздікті шеш:

\[\frac(x)(x-1)\le \frac(x-2)(x)\]

Шешім. Барлығын солға жылжыту:

\[\frac(x)(x-1)-\frac(x-2)(x)\le 0\]

Ортақ бөлгішке келтіреміз, жақшаларды ашамыз, алымдағы ұқсас мүшелерді береміз:

\[\бастау(туралау) & \frac(x\cdot x)(\left(x-1 \оң)\cdot x)-\frac(\left(x-2 \оң)\сол(x-1 \ оң жақ))(x\cdot \left(x-1 \right))\le 0; \\ & \frac(((x)^(2))-\left(((x)^(2))-2x-x+2 \right))(x\left(x-1 \оң)) \le0; \\ & \frac(((x)^(2))-((x)^(2))+3x-2)(x\left(x-1 \оң))\le 0; \\ & \frac(3x-2)(x\left(x-1 \оң))\le 0. \\\соңы(туралау)\]

Енді бізде классикалық бөлшек рационал теңсіздік бар, оны шешу қиын емес. Мен оны балама әдіспен - интервалдар әдісі арқылы шешуді ұсынамын:

\[\бастау(туралау) & \left(3x-2 \right)\cdot x\cdot \left(x-1 \right)=0; \\ & ((x)_(1))=\frac(2)(3);\ ((x)_(2))=0;\ ((x)_(3))=1. \\ \соңы(туралау)\]

Бөлгіштен келетін шектеуді ұмытпаңыз:

Сан жолында барлық сандар мен шектеулерді белгілейміз:

Барлық түбірлердің бірінші еселігі бар. Проблема жоқ. Біз жай ғана белгілерді қойып, қажетті жерлерді бояймыз:

Мұның бәрі. Жауабын жазуға болады.

Жауап. $x\in \left(-\infty ;0 \right)\bigcup \left[ (2)/(3)\;;1 \right)$.

Әрине, бұл өте қарапайым мысал болды. Ендеше, енді мәселені толығырақ қарастырайық. Айтпақшы, бұл тапсырманың деңгейі 8-сыныпта осы тақырып бойынша өз бетінше және бақылау жұмыстарымен толық сәйкес келеді.

Тапсырма. Теңсіздікті шеш:

\[\frac(1)((x)^(2))+8x-9)\ge \frac(1)(3((x)^(2))-5x+2)\]

Шешім. Барлығын солға жылжыту:

\[\frac(1)((x)^(2))+8x-9)-\frac(1)(3((x)^(2))-5x+2)\ge 0\]

Екі бөлшекті де ортақ бөлімге келтірмес бұрын, біз бұл бөлгіштерді көбейткіштерге бөлеміз. Кенеттен сол жақшалар шығады ма? Бірінші бөлгішпен бұл оңай:

\[((x)^(2))+8x-9=\сол(x-1 \оң)\сол(x+9 \оң)\]

Екіншісі сәл қиынырақ. Бөлшек табылған жақшаға тұрақты көбейткішті қосуға болады. Есіңізде болсын: бастапқы көпмүше бүтін коэффициенттерге ие болды, сондықтан көбейткіштерге бөлудің де бүтін коэффициенттерге ие болу ықтималдығы жоғары (шын мәнінде, дискриминант иррационалды болған жағдайдан басқа жағдайда ол әрқашан болады).

\[\бастау(туралау) & 3((x)^(2))-5x+2=3\left(x-1 \оң)\left(x-\frac(2)(3) \оң)= \\ & =\сол(x-1 \оң)\сол(3x-2 \оң) \соңы(туралау)\]

Көріп отырғаныңыздай, жалпы жақша бар: $\left(x-1 \right)$. Теңсіздікке оралып, екі бөлшекті де ортақ бөлгішке келтіреміз:

\[\бастау(туралау) & \frac(1)(\сол(x-1 \оң)\сол(x+9 \оң))-\frac(1)(\сол(x-1 \оң)\ left(3x-2\right))\ge 0; \\ & \frac(1\cdot \left(3x-2 \right)-1\cdot \left(x+9 \right))(\left(x-1 \right)\left(x+9 \right) )\left(3x-2 \right))\ge 0; \\ & \frac(3x-2-x-9)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ & \frac(2x-11)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ \соңы(туралау)\]

Бөлгішті нөлге қойыңыз:

\[\бастау(туралау) & \left(x-1 \right)\left(x+9 \right)\left(3x-2 \right)=0; \\ & x_(1)^(*)=1;\ x_(2)^(*)=-9;\ x_(3)^(*)=\frac(2)(3) \\ \end( туралау)\]

Көптік және сәйкес келетін түбірлер жоқ. Түзу сызықта төрт санды белгілейміз:

Біз белгілерді орналастырамыз:

Жауабын жазамыз.

Жауабы: $x\in \left(-\infty ;-9 \right)\bigcup \left((2)/(3)\;;1 \right)\bigcup \left[ 5,5;+\infty \ оң) $.

Барлығы! Осылайша, мен осы жолға дейін оқыдым. :)

Сызықтық теңсіздіктер деп аталадысол және оң бөліктері белгісіз мәнге қатысты сызықтық функциялар. Оларға, мысалы, теңсіздіктер жатады:

2х-1-x+3; 7x0;

5 >4 - 6x 9- x< x + 5 .

1) қатаң теңсіздіктер: ax+b>0немесе балта+б<0

2) Қатаң емес теңсіздіктер: ax+b≤0немесе балта+б≫ 0

Мына тапсырманы алайық. Параллелограмның бір қабырғасы 7 см. Параллелограммның периметрі 44 см-ден үлкен болуы үшін екінші қабырғасының ұзындығы қандай болуы керек?

Қалаған жағы болсын Xқараңыз Бұл жағдайда параллелограмның периметрі (14 + 2x) арқылы көрсетіледі.14 + 2x > 44 теңсіздігі параллелограммның периметрі есебінің математикалық моделі болып табылады. Егер осы теңсіздікте айнымалыны ауыстырамыз Xмысалы, 16 саны бойынша, содан кейін біз дұрыс сандық теңсіздікті аламыз 14 + 32\u003e 44. Бұл жағдайда біз 16 саны 14 + 2x\u003e 44 теңсіздігінің шешімі деп айтамыз.

Теңсіздіктің шешіміоны шынайы сандық теңсіздікке айналдыратын айнымалының мәнін атаңыз.

Сондықтан 15.1 сандарының әрқайсысы; 20;73 14 + 2x > 44 теңсіздігінің шешімі ретінде әрекет етеді, ал 10 саны, мысалы, оның шешімі емес.

Теңсіздікті шешуоның барлық шешімдерін орнату немесе шешімдердің жоқтығын дәлелдеу дегенді білдіреді.

Теңсіздіктің шешімін тұжырымдау теңдеудің түбірін тұжырымдауға ұқсас. Дегенмен, «теңсіздіктің түбірін» белгілеу әдеттегідей емес.

Сандық теңдіктердің қасиеттері теңдеулерді шешуге көмектесті. Сол сияқты, сандық теңсіздіктердің қасиеттері теңсіздіктерді шешуге көмектеседі.

Теңдеуді шеше отырып, біз оны басқа, қарапайым, бірақ берілген теңдеумен теңестіреміз. Сол сияқты, теңсіздіктерге жауап табылады. Теңдеуді оған эквивалентті теңдеуге өзгерту кезінде олар теңдеудің бір бөлігінен қарама-қарсы жаққа мүшелерді көшіру және теңдеудің екі бөлігін бірдей нөлдік емес санға көбейту туралы теореманы пайдаланады. Теңсіздікті шешу кезінде оның теңдеуден айтарлықтай айырмашылығы бар, ол теңдеудің кез келген шешімін оны бастапқы теңдеуге ауыстыру арқылы тексеруге болатынында жатыр. Теңсіздіктерде мұндай әдіс жоқ, өйткені бастапқы теңсіздікке шешімдердің шексіз санын ауыстыру мүмкін емес. Сондықтан маңызды тұжырымдама бар, бұл көрсеткілер<=>эквивалентті немесе эквивалентті түрлендірулердің белгісі болып табылады. Трансформация деп аталады эквивалентнемесе эквивалентегер олар шешім жинағын өзгертпесе.

Теңсіздіктерді шешудің ұқсас ережелері.

Егер қандай да бір мүше таңбасын қарама-қарсысымен ауыстыра отырып, теңсіздіктің бір бөлігінен екінші бөлігіне ауыстырылса, онда берілгенге эквивалентті теңсіздікті аламыз.

Егер теңсіздіктің екі бөлігі де бірдей оң санға көбейтілсе (бөлінсе), онда берілгенге эквивалентті теңсіздікті аламыз.

Егер теңсіздік таңбасын қарама-қарсысына ауыстыра отырып, теңсіздіктің екі бөлігі де бірдей теріс санға көбейтілсе (бөлінсе), онда берілгенге эквивалент теңсіздікті аламыз.

Бұларды пайдалану ережелеркелесі теңсіздіктерді есептейміз.

1) Теңсіздікті талдап көрейік 2x - 5 > 9.

Бұл сызықтық теңсіздік, оның шешімін тауып, негізгі ұғымдарды талқылаңыз.

2x - 5 > 9<=>2x > 14(5 қарама-қарсы таңбамен сол жаққа жылжытылды), содан кейін біз бәрін 2-ге бөлдік және бізде бар x > 7. Біз оське шешімдер жиынтығын қолданамыз x

Біз оң бағытталған сәулені алдық. Шешімдер жиынын теңсіздік түрінде де белгілейміз x > 7, немесе x(7; ∞) интервалы ретінде. Және бұл теңсіздіктің нақты шешімі қандай? Мысалға, x=10бұл теңсіздіктің ерекше шешімі, x=12да осы теңсіздіктің ерекше шешімі болып табылады.

Көптеген нақты шешімдер бар, бірақ біздің міндетіміз барлық шешімдерді табу. Ал шешімдер әдетте шексіз.

Талдап көрейік 2 мысал:

2) Теңсіздікті шеш 4a - 11 > a + 13.

Оны шешейік: абір жаққа жылжытыңыз 11 екінші жағына жылжи отырып, біз 3а аламыз< 24, и в результате после деления обеих частей на 3 теңсіздік формасы болады а<8 .

4a - 11 > a + 13<=>3а< 24 <=>а< 8 .

Біз жиынтықты да көрсетеміз а< 8 , бірақ қазірдің өзінде осьте а.

Жауабы а теңсіздігі түрінде жазылады< 8, либо а(-∞;8), 8 қосылмайды.

Аралық әдісбөлшек рационал теңсіздіктерді шешудің қарапайым тәсілі болып табылады. Бұл айнымалыға тәуелді рационал (немесе бөлшек-рационал) өрнектері бар теңсіздіктердің атауы.

1. Мысалы, келесі теңсіздікті қарастырайық

Интервал әдісі оны бірнеше минут ішінде шешуге мүмкіндік береді.

Бұл теңсіздіктің сол жағында бөлшек рационал функция орналасқан. Рационалды, өйткені оның құрамында түбірлер де, синустар да, логарифмдер де жоқ – тек рационал өрнектер. Оң жақта нөл.

Интервал әдісі бөлшек рационал функцияның келесі қасиетіне негізделген.

Бөлшек рационал функция таңбаны нөлге тең немесе жоқ нүктелерде ғана өзгерте алады.

Квадрат үшмүшенің көбейткіштерге жіктелуін, яғни түрінің өрнегін еске түсіріңіз.

Мұндағы және квадрат теңдеудің түбірлері.

Біз ось саламыз және алым мен бөлгіш жойылатын нүктелерді орналастырамыз.

Бөлгіштің нөлдері және тесілген нүктелер, өйткені бұл нүктелерде теңсіздіктің сол жағындағы функция анықталмаған (нөлге бөлуге болмайды). Алым және - нөлдері көлеңкеленген, өйткені теңсіздік қатаң емес. For және біздің теңсіздігіміз қанағаттандырылады, өйткені оның екі бөлігі де нөлге тең.

Бұл нүктелер осьтерді аралықтарға бөледі.

Осы интервалдардың әрқайсысы бойынша теңсіздігіміздің сол жағындағы бөлшек-рационал функцияның таңбасын анықтайық. Бөлшек рационал функциясы нөлге тең немесе жоқ нүктелерде ғана таңбасын өзгерте алатынын есте ұстаймыз. Бұл алым немесе бөлгіш жойылатын нүктелер арасындағы аралықтардың әрқайсысында теңсіздіктің сол жағындағы өрнектің таңбасы тұрақты болады - «плюс» немесе «минус».

Сондықтан әрбір осындай интервалдағы функцияның таңбасын анықтау үшін осы интервалға жататын кез келген нүктені аламыз. Бізге сәйкес келетіні.
. Мысалы, теңсіздіктің сол жағындағы өрнектің таңбасын тексеріңіз. «Жақшалардың» әрқайсысы теріс. Сол жағында белгі бар.

Келесі аралық: . белгісін тексеріп көрейік. Сол жақ таңбаға өзгергенін түсінеміз.

Алайық. Өрнек оң болғанда - демек, -ден -ге дейінгі барлық интервалда ол оң болады.

, үшін теңсіздіктің сол жағы теріс.

Соңында class="tex" alt="(!LANG:x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Өрнектің қандай интервалдарда оң болатынын таптық. Жауапты жазу қалды:

Жауап: .

Назар аударыңыз: интервалдардағы белгілер кезектесіп тұрады. Бұл болды, өйткені әрбір нүктеден өткенде сызықтық факторлардың дәл біреуі таңбасын өзгертті, ал қалғандары оны өзгеріссіз қалдырды.

Интервалдық әдіс өте қарапайым екенін көреміз. Бөлшек-рационал теңсіздікті интервалдар әдісімен шешу үшін оны келесі түрге келтіреміз:

Немесе class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle P\left(x \оң))(\displaystyle Q\left(x \оң)) > 0"> !}, немесе .

(сол жағында – бөлшек-рационал функция, оң жағында – нөл).

Содан кейін - сан түзуінде алым немесе бөлгіш жойылатын нүктелерді белгілейміз.
Бұл нүктелер бүкіл сан түзуін интервалдарға бөледі, олардың әрқайсысында бөлшек-рационал функция таңбасын сақтайды.
Әр интервалда оның белгісін білу ғана қалады.
Мұны берілген аралықтағы кез келген нүктедегі өрнектің таңбасын тексеру арқылы орындаймыз. Осыдан кейін біз жауапты жазамыз. Осымен болды.

Бірақ сұрақ туындайды: белгілер әрқашан кезектесе ме? Жоқ әрқашан емес! Біз белгілерді механикалық және ойланбай қоюдан сақ болуымыз керек.

2. Тағы бір теңсіздікті қарастырайық.

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle \left(x-2 \right)^2)(\displaystyle \сол(x-1 \оң)) \left(x-3\right))>0"> !}

Біз қайтадан нүктелерді оське орналастырамыз. және нүктелері тесілген, себебі олар бөлгіштің нөлдері. Теңсіздік қатаң болғандықтан, нүкте де тесілген.

Алым оң болғанда, бөлгіштегі екі көбейткіш те теріс болады. Бұл берілген аралықтан кез келген санды алу арқылы оңай тексеруге болады, мысалы, . Сол жағында белгі бар:

Алым оң болғанда; бөлгіштегі бірінші фактор оң, екінші фактор теріс. Сол жағында белгі бар:

Жағдай бірдей болғанда! Алым оң, бөлгіштегі бірінші көбейткіш оң, екіншісі теріс. Сол жағында белгі бар:

Соңында, class="tex" alt="(!LANG:x>3) көмегімен"> все множители положительны, и левая часть имеет знак :!}

Жауап: .

Кейіпкерлердің алмасуы неге бұзылды? Өйткені нүктеден өткенде көбейткіш оған «жауапты». белгісін өзгертпеді. Демек, теңсіздігіміздің сол жағы да таңбасын өзгерткен жоқ.

Шығару: егер сызықтық коэффициент жұп дәрежеде болса (мысалы, шаршыда), онда нүкте арқылы өткенде сол жақтағы өрнектің таңбасы өзгермейді. Тақ дәрежеде белгі, әрине, өзгереді.

3. Күрделі істі қарастырайық. Оның алдыңғысынан айырмашылығы: теңсіздік қатаң емес:

Сол жағы алдыңғы мәселедегідей. Белгілердің суреті бірдей болады:

Мүмкін жауап бірдей болар? Жоқ! Шешім қосылды. Бұл теңсіздіктің сол және оң жақтары да нөлге тең болғандықтан, бұл нүкте шешім болып табылады.

Жауап: .

Математикадан емтихан мәселесінде мұндай жағдай жиі кездеседі. Мұнда талапкерлер тұзаққа түсіп, ұпай жоғалтады. Сақ болыңыз!

4. Алым немесе бөлгішті сызықтық көбейткіштерге бөлу мүмкін болмаса ше? Мына теңсіздікті қарастырайық:

Квадрат үшмүшені көбейткіштерге бөлуге болмайды: дискриминант теріс, түбірлері жоқ. Бірақ бұл жақсы! Бұл өрнектің белгісі барлығына бірдей, нақтырақ айтсақ, оң екенін білдіреді. Бұл туралы толығырақ квадраттық функцияның қасиеттері туралы мақаладан оқи аласыз.

Ал енді теңсіздігіміздің екі жағын барлығына оң мәнге бөлуге болады . Эквивалентті теңсіздікке келеміз:

Бұл интервал әдісімен оңай шешіледі.

Назар аударыңыз – теңсіздіктің екі жағын да оң екенін анық білген мәнге бөлдік. Әрине, жалпы жағдайда теңсіздікті таңбасы белгісіз айнымалыға көбейтуге немесе бөлуге болмайды.

5 . Қарапайым болып көрінетін басқа теңсіздікті қарастырайық:

Сондықтан мен оны көбейткім келеді. Бірақ біз қазірдің өзінде ақылдымыз және біз мұны істемейміз. Өйткені, бұл оң және теріс болуы мүмкін. Ал егер теңсіздіктің екі бөлігін де теріс мәнге көбейтсе, теңсіздіктің таңбасы өзгеретінін білеміз.

Біз басқаша әрекет етеміз - біз бәрін бір бөлікке жинап, оны ортақ бөлгішке жеткіземіз. Нөл оң жақта қалады:

Class="tex" alt="(!LANG:\genfrac()()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}

Ал одан кейін - қолданылады интервал әдісі.

Теңсіздіктерді желіде шешу

Теңсіздіктерді шешудің алдында теңдеулердің қалай шешілетінін жақсы түсіну керек.

Теңсіздіктің қатаң () немесе қатаң емес (≤, ≥) екендігі маңызды емес, бірінші қадам теңсіздік белгісін теңдікпен (=) ауыстыру арқылы теңдеуді шешу керек.

Теңсіздікті шешу нені білдіретінін түсіндіріңіз?

Теңдеулерді зерттегеннен кейін студенттің басында мынадай сурет пайда болады: теңдеудің екі бөлігі де бірдей мәндерді қабылдайтын айнымалының мәндерін табу керек. Басқаша айтқанда, теңдік орындалатын барлық нүктелерді табыңыз. Барлығы дұрыс!

Теңсіздіктер туралы айтқанда, олар теңсіздік орындалатын аралықтарды (сегменттерді) табуды білдіреді. Егер теңсіздікте екі айнымалы болса, онда шешім енді интервалдар емес, жазықтықтағы кейбір аймақтар болады. Үш айнымалыдағы теңсіздіктің шешімі қандай болатынын тап?

Теңсіздіктерді қалай шешуге болады?

Интервалдар әдісі (яғни интервалдар әдісі) теңсіздіктерді шешудің әмбебап тәсілі болып саналады, ол берілген теңсіздік орындалатын барлық интервалдарды анықтаудан тұрады.

Теңсіздіктің түріне бармай-ақ, бұл жағдайда оның мәні емес, сәйкес теңдеуді шешу және оның түбірлерін анықтау, содан кейін осы шешімдерді сандық осьте белгілеу қажет.

Теңсіздіктің шешімін жазудың дұрыс жолы қандай?

Теңсіздікті шешу аралықтарын анықтағаннан кейін шешімнің өзін дұрыс жазу керек. Маңызды нюанс бар - интервалдардың шекаралары шешімге кіреді ме?

Мұнда бәрі қарапайым. Егер теңдеудің шешімі ОДЖ-ны қанағаттандырса және теңсіздік қатаң болмаса, онда интервал шекарасы теңсіздіктің шешіміне кіреді. Әйтпесе, жоқ.

Әрбір интервалды қарастыратын болсақ, теңсіздіктің шешімі интервалдың өзі немесе жарты интервал (оның шекараларының бірі теңсіздікті қанағаттандыратын кезде) немесе кесінді - шекараларымен бірге интервал болуы мүмкін.

Маңызды нүкте

Тек интервалдар, жарты интервалдар және кесінділер теңсіздіктің шешімі бола алады деп ойламаңыз. Жоқ, шешімге жеке нүктелерді де қосуға болады.

Мысалы, |x|≤0 теңсіздігінің бір ғана шешімі бар - 0 нүктесі.

Және |x| теңсіздігі

Теңсіздік калькуляторы не үшін қажет?

Теңсіздік калькуляторы дұрыс қорытынды жауапты береді. Бұл жағдайда көп жағдайда сандық осьтің немесе жазықтықтың иллюстрациясы беріледі. Сіз аралықтардың шекараларының шешімге қосылғанын немесе кірмейтінін көре аласыз - нүктелер толтырылған немесе тесілген түрде көрсетіледі.

Онлайн теңсіздік калькуляторының арқасында сіз теңдеудің түбірлерін дұрыс тапқаныңызды, оларды сандар сызығында белгілегеніңізді және интервалдардағы (және шекаралардағы) теңсіздік шарттарын тексергеніңізді тексере аласыз ба?

Егер сіздің жауабыңыз калькулятордың жауабынан өзгеше болса, онда сіз өз шешіміңізді екі рет тексеріп, жіберілген қатені анықтауыңыз керек.