Aide sur Tele2, tarifs, questions

Ceux qui s'intéressent à l'histoire du théorème de Pythagore, étudié dans le programme scolaire, seront également curieux de connaître un fait tel que la publication en 1940 d'un livre contenant trois cent soixante-dix preuves de ce théorème apparemment simple. Mais cela a intrigué l’esprit de nombreux mathématiciens et philosophes de différentes époques. Dans le Livre Guinness des Records, il est enregistré comme le théorème avec le nombre maximum de preuves.

Histoire du théorème de Pythagore

Associé au nom de Pythagore, le théorème était connu bien avant la naissance du grand philosophe. Ainsi, en Égypte, lors de la construction de structures, le rapport d'aspect d'un triangle rectangle était pris en compte il y a cinq mille ans. Les textes babyloniens mentionnent le même rapport hauteur/largeur d'un triangle rectangle 1200 ans avant la naissance de Pythagore.

La question se pose, pourquoi alors l'histoire dit-elle que l'origine du théorème de Pythagore lui appartient ? Il ne peut y avoir qu'une seule réponse : il a prouvé le rapport des côtés d'un triangle. Il a fait ce que ceux qui utilisaient simplement le rapport hauteur/largeur et l'hypoténuse établis par l'expérience n'avaient pas fait il y a des siècles.

De la vie de Pythagore

Le futur grand scientifique, mathématicien, philosophe est né sur l'île de Samos en 570 avant JC. Les documents historiques ont conservé des informations sur le père de Pythagore, qui était sculpteur de pierres précieuses, mais il n'y a aucune information sur sa mère. Ils ont dit du garçon qui est né qu'il était un enfant extraordinaire qui montrait une passion pour la musique et la poésie dès son enfance. Les historiens incluent Hermodamas et Phérécyde de Syros comme professeurs du jeune Pythagore. Le premier a introduit le garçon dans le monde des muses, et le second, philosophe et fondateur de l’école de philosophie italienne, a dirigé le regard du jeune homme vers le logos.

À l'âge de 22 ans (548 avant JC), Pythagore se rend à Naucratis pour étudier la langue et la religion des Égyptiens. Ensuite, son chemin s'est arrêté à Memphis, où, grâce aux prêtres, après avoir subi leurs ingénieux tests, il a compris la géométrie égyptienne, ce qui a peut-être incité le jeune homme curieux à prouver le théorème de Pythagore. L’histoire attribuera plus tard ce nom au théorème.

Captivité du roi de Babylone

Sur le chemin du retour en Hellas, Pythagore est capturé par le roi de Babylone. Mais le fait d'être en captivité a profité à l'esprit curieux du mathématicien en herbe : il avait beaucoup à apprendre. En effet, à cette époque, les mathématiques à Babylone étaient plus développées qu’en Égypte. Il a passé douze ans à étudier les mathématiques, la géométrie et la magie. Et c'est peut-être la géométrie babylonienne qui a été impliquée dans la preuve du rapport des côtés d'un triangle et dans l'histoire de la découverte du théorème. Pythagore avait suffisamment de connaissances et de temps pour cela. Mais il n’existe aucune confirmation ou réfutation documentaire de ce qui s’est produit à Babylone.

En 530 avant JC. Pythagore s'échappe de captivité vers son pays natal, où il vit à la cour du tyran Polycrate dans le statut de semi-esclave. Pythagore ne se contente pas d'une telle vie, et il se retire dans les grottes de Samos, puis se rend dans le sud de l'Italie, où se trouvait alors la colonie grecque de Croton.

Ordre monastique secret

Sur la base de cette colonie, Pythagore organisa un ordre monastique secret, qui était à la fois une union religieuse et une société scientifique. Cette société avait sa propre charte, qui parlait du respect d'un mode de vie particulier.

Pythagore a soutenu que pour comprendre Dieu, une personne doit connaître des sciences telles que l'algèbre et la géométrie, connaître l'astronomie et comprendre la musique. Les travaux de recherche se résumaient à la connaissance du côté mystique des nombres et de la philosophie. Il convient de noter que les principes prêchés à cette époque par Pythagore ont aujourd’hui un sens en termes d’imitation.

De nombreuses découvertes faites par les étudiants de Pythagore lui sont attribuées. Cependant, en bref, l'histoire de la création du théorème de Pythagore par les historiens et biographes anciens de l'époque est directement associée au nom de ce philosophe, penseur et mathématicien.

Enseignements de Pythagore

Peut-être que l'idée du lien entre le théorème et le nom de Pythagore a été motivée par la déclaration du grand Grec selon laquelle tous les phénomènes de notre vie sont cryptés dans le fameux triangle avec ses jambes et son hypoténuse. Et ce triangle est la « clé » pour résoudre tous les problèmes émergents. Le grand philosophe a dit qu’il faut voir le triangle, alors on peut considérer que le problème est résolu aux deux tiers.

Pythagore ne parlait de son enseignement qu'à ses étudiants oralement, sans prendre de notes et en le gardant secret. Malheureusement, les enseignements du plus grand philosophe n'ont pas survécu jusqu'à nos jours. Quelque chose s'en est échappé, mais il est impossible de dire ce qui est vrai et ce qui est faux dans ce qui est devenu connu. Même avec l’histoire du théorème de Pythagore, tout n’est pas certain. Les historiens des mathématiques doutent de la paternité de Pythagore ; à leur avis, le théorème a été utilisé plusieurs siècles avant sa naissance.

théorème de Pythagore

Cela peut paraître étrange, mais il n'existe aucun fait historique prouvant le théorème de Pythagore lui-même - ni dans les archives ni dans aucune autre source. Dans la version moderne, on pense qu’il n’appartient qu’à Euclide lui-même.

Il existe des preuves provenant de l'un des plus grands historiens des mathématiques, Moritz Cantor, qui a découvert sur un papyrus conservé au musée de Berlin des écrits écrits par les Égyptiens vers 2300 avant JC. e. égalité, qui se lit comme suit : 3² + 4² = 5².

Bref historique du théorème de Pythagore

La formulation du théorème des « Principes » euclidiens, en traduction, sonne de la même manière que dans l'interprétation moderne. Il n'y a rien de nouveau dans sa lecture : le carré du côté opposé à l'angle droit est égal à la somme des carrés des côtés adjacents à l'angle droit. Le fait que les anciennes civilisations de l'Inde et de la Chine utilisaient le théorème est confirmé par le traité « Zhou - bi suan jin ». Il contient des informations sur le triangle égyptien, qui décrit le rapport hauteur/largeur comme 3:4:5.

Non moins intéressant est un autre livre mathématique chinois, « Chu Pei », qui mentionne également le triangle de Pythagore avec des explications et des dessins qui coïncident avec les dessins de géométrie hindoue de Bashara. À propos du triangle lui-même, le livre dit que si un angle droit peut être décomposé en ses éléments constitutifs, alors la ligne qui relie les extrémités des côtés sera égale à cinq si la base est égale à trois et la hauteur est égale à quatre. .

Traité indien "Sulva Sutra", datant d'environ 7e-5e siècles avant JC. e., parle de construire un angle droit en utilisant le triangle égyptien.

Preuve du théorème

Au Moyen Âge, les étudiants considéraient que prouver un théorème était trop difficile. Les élèves faibles apprenaient les théorèmes par cœur, sans comprendre le sens de la preuve. À cet égard, ils ont reçu le surnom de « ânes », car le théorème de Pythagore était pour eux un obstacle insurmontable, comme un pont pour un âne. Au Moyen Âge, les étudiants inventaient un vers humoristique au sujet de ce théorème.

Pour prouver le théorème de Pythagore de la manière la plus simple, vous devez simplement mesurer ses côtés, sans utiliser le concept d'aire dans la preuve. La longueur du côté opposé à l'angle droit est c, et a et b lui sont adjacents, nous obtenons ainsi l'équation : a 2 + b 2 = c 2. Cette affirmation, comme mentionné ci-dessus, est vérifiée en mesurant la longueur des côtés d'un triangle rectangle.

Si l'on commence la preuve du théorème en considérant l'aire des rectangles construits sur les côtés du triangle, on peut déterminer l'aire de la figure entière. Elle sera égale à l'aire d'un carré de côté (a+b), et d'autre part, à la somme des aires de quatre triangles et du carré intérieur.

(une + b) 2 = 4 x ab/2 + c 2 ;

une 2 + 2ab + b 2 ;

c 2 = a 2 + b 2 , ce qui devait être prouvé.

L’importance pratique du théorème de Pythagore est qu’il peut être utilisé pour trouver la longueur des segments sans les mesurer. Lors de la construction des structures, les distances, le placement des supports et des poutres sont calculés et les centres de gravité sont déterminés. Le théorème de Pythagore est également appliqué à toutes les technologies modernes. Ils n'ont pas oublié le théorème lors de la création de films en dimensions 3D-6D, où en plus des trois dimensions auxquelles nous sommes habitués : la hauteur, la longueur, la largeur, le temps, l'odeur et le goût sont pris en compte. Quel est le lien entre les goûts et les odeurs et le théorème, demandez-vous ? Tout est très simple - lors de la projection d'un film, vous devez calculer où et quelles odeurs et quels goûts diriger dans la salle.

Ce n'est que le début. Des possibilités illimitées de découverte et de création de nouvelles technologies attendent les esprits curieux.

théorème de Pythagore- un des théorèmes fondamentaux de la géométrie euclidienne, établissant la relation

entre les côtés d'un triangle rectangle.

On pense que cela a été prouvé par le mathématicien grec Pythagore, qui lui a donné son nom.

Formulation géométrique du théorème de Pythagore.

Le théorème était initialement formulé comme suit :

Dans un triangle rectangle, l'aire du carré construit sur l'hypoténuse est égale à la somme des aires des carrés,

construit sur pieds.

Formulation algébrique du théorème de Pythagore.

Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des jambes.

Autrement dit, désignant la longueur de l'hypoténuse du triangle par c, et les longueurs des jambes à travers un Et b:

Les deux formules théorème de Pythagore sont équivalents, mais la seconde formulation est plus élémentaire, elle ne

nécessite la notion de zone. Autrement dit, la deuxième affirmation peut être vérifiée sans rien savoir de la zone et

en mesurant uniquement les longueurs des côtés d'un triangle rectangle.

Théorème de Pythagore inverse.

Si le carré d’un côté d’un triangle est égal à la somme des carrés des deux autres côtés, alors

triangle rectangle.

Ou, en d'autres termes :

Pour chaque triple de nombres positifs un, b Et c, tel que

il y a un triangle rectangle avec des jambes un Et b et l'hypoténuse c.

Théorème de Pythagore pour un triangle isocèle.

Théorème de Pythagore pour un triangle équilatéral.

Preuves du théorème de Pythagore.

Actuellement, 367 preuves de ce théorème ont été enregistrées dans la littérature scientifique. Probablement le théorème

Pythagore est le seul théorème avec un nombre de preuves aussi impressionnant. Une telle diversité

ne peut s'expliquer que par la signification fondamentale du théorème pour la géométrie.

Bien entendu, conceptuellement, ils peuvent tous être divisés en un petit nombre de classes. Les plus célèbres d'entre eux :

preuve méthode de zone, axiomatique Et preuve exotique(Par exemple,

en utilisant équations différentielles).

1. Preuve du théorème de Pythagore en utilisant des triangles similaires.

La preuve suivante de la formulation algébrique est la plus simple des preuves construites

directement à partir des axiomes. En particulier, il n’utilise pas la notion d’aire d’une figure.

Laisser abc il y a un triangle rectangle avec un angle droit C. Tirons la hauteur de C et désigne

sa fondation à travers H.

Triangle ACH semblable à un triangle UN B C aux deux coins. De même, le triangle CBH similaire abc.

En introduisant la notation :

on a:

,

ce qui correspond à -

Plié un 2 et b 2, on obtient :

ou , ce qui devait être prouvé.

2. Preuve du théorème de Pythagore par la méthode des aires.

Les preuves ci-dessous, malgré leur apparente simplicité, ne sont pas du tout si simples. Tous

utiliser des propriétés d'aire dont les preuves sont plus complexes que la preuve du théorème de Pythagore lui-même.

• Preuve par équicomplémentarité.

Disposons quatre rectangles égaux

triangle comme indiqué sur la figure

sur la droite.

Quadrangle à côtés c- carré,

puisque la somme de deux angles aigus est de 90°, et

angle déplié - 180°.

L'aire de la figure entière est égale, d'une part,

aire d'un carré de côté ( a+b), et d’autre part, la somme des aires de quatre triangles et

Q.E.D.

3. Preuve du théorème de Pythagore par la méthode infinitésimale.

​

En regardant le dessin montré sur la figure et

je regarde le changement de côtéun, nous pouvons

écrire la relation suivante pour l'infini

petit incréments latérauxAvec Et un(en utilisant la similarité

Triangles):

En utilisant la méthode de séparation des variables, on trouve :

Une expression plus générale pour la modification de l'hypoténuse en cas d'incréments des deux côtés :

En intégrant cette équation et en utilisant les conditions initiales, on obtient :

On arrive ainsi à la réponse souhaitée :

Comme il est facile de le constater, la dépendance quadratique dans la formule finale apparaît en raison de la relation linéaire

proportionnalité entre les côtés du triangle et les incréments, tandis que la somme est liée aux indépendants

contributions provenant de l'augmentation des différentes jambes.

Une preuve plus simple peut être obtenue si l’on suppose que l’une des jambes ne subit pas d’augmentation

(dans ce cas la jambe b). Alors pour la constante d’intégration on obtient :

Histoire

Chu-pei 500-200 avant JC. A gauche se trouve l'inscription : la somme des carrés des longueurs de la hauteur et de la base est le carré de la longueur de l'hypoténuse.

Dans l'ancien livre chinois Chu-pei ( Anglais) (chinois 周髀算經) parle d'un triangle de Pythagore ayant des côtés 3, 4 et 5. Le même livre propose un dessin qui coïncide avec l'un des dessins de la géométrie hindoue de Bashara.

Vers 400 avant JC. J.-C., selon Proclus, Platon a donné une méthode pour trouver les triplets pythagoriciens, combinant algèbre et géométrie. Vers 300 avant JC. e. La plus ancienne preuve axiomatique du théorème de Pythagore apparaît dans les Éléments d'Euclide.

Formulations

Formulation géométrique :

Le théorème était initialement formulé comme suit :

Formulation algébrique :

Autrement dit, désignant la longueur de l'hypoténuse du triangle par , et les longueurs des jambes par et :

Les deux formulations du théorème sont équivalentes, mais la seconde formulation est plus élémentaire ; elle ne nécessite pas la notion d'aire. Autrement dit, la deuxième affirmation peut être vérifiée sans rien connaître de l’aire et en mesurant uniquement les longueurs des côtés d’un triangle rectangle.

Théorème de Pythagore inverse :

Pour tout triplet de nombres positifs, et, tel que, il existe un triangle rectangle avec les pattes et et l'hypoténuse.

Preuve

À l'heure actuelle, 367 preuves de ce théorème ont été enregistrées dans la littérature scientifique. Le théorème de Pythagore est probablement le seul théorème avec un nombre de preuves aussi impressionnant. Une telle diversité ne peut s’expliquer que par l’importance fondamentale du théorème pour la géométrie.

Bien entendu, conceptuellement, ils peuvent tous être divisés en un petit nombre de classes. Les plus connues d'entre elles : les preuves par la méthode des aires, les preuves axiomatiques et exotiques (par exemple, utilisant des équations différentielles).

À travers des triangles similaires

La preuve suivante de la formulation algébrique est la plus simple des preuves, construite directement à partir des axiomes. En particulier, il n’utilise pas la notion d’aire d’une figure.

Laisser abc il y a un triangle rectangle avec un angle droit C. Tirons la hauteur de C et désignons sa base par H. Triangle ACH semblable à un triangle abcà deux coins. De même, le triangle CBH similaire abc. En introduisant la notation

on a

Qu'est-ce qui est équivalent

En additionnant, nous obtenons

, c'est ce qu'il fallait prouver

Preuves utilisant la méthode des aires

Les preuves ci-dessous, malgré leur apparente simplicité, ne sont pas du tout si simples. Ils utilisent tous des propriétés d’aire dont la preuve est plus complexe que la preuve du théorème de Pythagore lui-même.

Preuve par équicomplémentation

1. Disposons quatre triangles rectangles égaux comme le montre la figure 1.
2. Quadrangle à côtés c est un carré, puisque la somme de deux angles aigus est de 90° et l’angle droit est de 180°.
3. L'aire de la figure entière est égale, d'une part, à l'aire d'un carré de côté (a + b), et d'autre part, à la somme des aires des quatre triangles et du superficie du carré intérieur.

Q.E.D.

La preuve d'Euclide

L'idée de la preuve d'Euclide est la suivante : essayons de prouver que la moitié de l'aire du carré construit sur l'hypoténuse est égale à la somme des demi-aires des carrés construits sur les jambes, puis les aires de le grand et les deux petits carrés sont égaux.

Regardons le dessin de gauche. Sur celui-ci, nous avons construit des carrés sur les côtés d'un triangle rectangle et tracé un rayon s partant du sommet de l'angle droit C perpendiculaire à l'hypoténuse AB, il coupe le carré ABIK, construit sur l'hypoténuse, en deux rectangles - BHJI et HAKJ, respectivement. Il s'avère que les aires de ces rectangles sont exactement égales aux aires des carrés construits sur les pattes correspondantes.

Essayons de prouver que l'aire du carré DECA est égale à l'aire du rectangle AHJK. Pour ce faire, nous utiliserons une observation auxiliaire : L'aire d'un triangle de même hauteur et base que le rectangle donné est égal à la moitié de l'aire du rectangle donné. C'est une conséquence de la définition de l'aire d'un triangle comme la moitié du produit de la base et de la hauteur. De cette observation, il s'ensuit que l'aire du triangle ACK est égale à l'aire du triangle AHK (non représenté sur la figure), qui à son tour est égale à la moitié de l'aire du rectangle AHJK.

Montrons maintenant que l'aire du triangle ACK est également égale à la moitié de l'aire du carré DECA. La seule chose à faire pour cela est de prouver l'égalité des triangles ACK et BDA (puisque l'aire du triangle BDA est égale à la moitié de l'aire du carré selon la propriété ci-dessus). Cette égalité est évidente : les triangles sont égaux des deux côtés ainsi que l'angle qui les sépare. A savoir - AB=AK, AD=AC - l'égalité des angles CAK et BAD est facile à prouver par la méthode du mouvement : on fait tourner le triangle CAK de 90° dans le sens inverse des aiguilles d'une montre, alors il est évident que les côtés correspondants des deux triangles dans la question coïncidera (du fait que l’angle au sommet du carré est de 90°).

Le raisonnement pour l’égalité des aires du carré BCFG et du rectangle BHJI est tout à fait similaire.

Ainsi, nous avons prouvé que l'aire d'un carré construit sur l'hypoténuse est composée des aires des carrés construits sur les jambes. L'idée derrière cette preuve est illustrée davantage par l'animation ci-dessus.

Preuve de Léonard de Vinci

Les principaux éléments de la preuve sont la symétrie et le mouvement.

Considérons le dessin, comme le montre la symétrie, le segment coupe le carré en deux parties identiques (puisque les triangles sont de construction égale).

En effectuant une rotation de 90 degrés dans le sens inverse des aiguilles d'une montre autour du point, nous voyons l'égalité des chiffres ombrés et.

Il est maintenant clair que l'aire de la figure que nous avons ombrée est égale à la somme de la moitié des aires des petits carrés (construits sur les pattes) et de l'aire du triangle d'origine. En revanche, elle est égale à la moitié de l'aire du grand carré (construit sur l'hypoténuse) plus l'aire du triangle d'origine. Ainsi, la moitié de la somme des aires des petits carrés est égale à la moitié de l'aire du grand carré, et donc la somme des aires des carrés construits sur les pattes est égale à l'aire du carré construit sur le hypoténuse.

Preuve par la méthode infinitésimale

La preuve suivante utilisant des équations différentielles est souvent attribuée au célèbre mathématicien anglais Hardy, qui a vécu dans la première moitié du 20e siècle.

En regardant le dessin montré sur la figure et en observant le changement de côté un, on peut écrire la relation suivante pour des incréments de côté infinitésimaux Avec Et un(en utilisant la similarité triangulaire):

En utilisant la méthode de séparation des variables, on trouve

Une expression plus générale pour le changement de l'hypoténuse en cas d'incréments des deux côtés

En intégrant cette équation et en utilisant les conditions initiales, on obtient

On arrive ainsi à la réponse souhaitée

Comme il est facile de le voir, la dépendance quadratique dans la formule finale apparaît en raison de la proportionnalité linéaire entre les côtés du triangle et les incréments, tandis que la somme est associée à des contributions indépendantes de l'incrément des différentes jambes.

Une preuve plus simple peut être obtenue si l'on suppose que l'une des jambes ne subit pas d'incrément (dans ce cas la jambe). Alors pour la constante d’intégration on obtient

Variations et généralisations

Formes géométriques similaires sur trois côtés

Généralisation pour des triangles semblables, aire de formes vertes A + B = aire de bleu C

Théorème de Pythagore utilisant des triangles rectangles similaires

Euclide a généralisé le théorème de Pythagore dans son œuvre Les débuts, en élargissant les aires des carrés sur les côtés aux aires de figures géométriques similaires :

Si nous construisons des figures géométriques similaires (voir Géométrie euclidienne) sur les côtés d'un triangle rectangle, alors la somme des deux figures plus petites sera égale à l'aire de la plus grande figure.

L'idée principale de cette généralisation est que l'aire d'une telle figure géométrique est proportionnelle au carré de l'une de ses dimensions linéaires et, en particulier, au carré de la longueur de n'importe quel côté. Par conséquent, pour des figures similaires avec des aires UN, B Et C construit sur les côtés avec la longueur un, b Et c, nous avons:

Mais d’après le théorème de Pythagore : un 2 + b 2 = c 2 alors UN + B = C.

A l’inverse, si l’on peut prouver que UN + B = C pour trois figures géométriques similaires sans utiliser le théorème de Pythagore, nous pouvons alors prouver le théorème lui-même, en se déplaçant dans la direction opposée. Par exemple, le triangle central de départ peut être réutilisé comme triangle C sur l'hypoténuse, et deux triangles rectangles similaires ( UN Et B), construit sur les deux autres côtés, formés en divisant le triangle central par sa hauteur. La somme des aires des deux plus petits triangles est alors évidemment égale à l'aire du troisième, donc UN + B = C et, en effectuant la preuve précédente dans l'ordre inverse, nous obtenons le théorème de Pythagore a 2 + b 2 = c 2 .

Théorème du cosinus

Le théorème de Pythagore est un cas particulier du théorème du cosinus plus général, qui relie les longueurs des côtés dans un triangle arbitraire :

où θ est l'angle entre les côtés un Et b.

Si θ est de 90 degrés alors cos θ = 0 et la formule se simplifie en théorème de Pythagore habituel.

Triangle gratuit

Vers n'importe quel coin sélectionné d'un triangle arbitraire avec des côtés une, b, c Inscrivons un triangle isocèle de telle sorte que les angles égaux à sa base θ soient égaux à l'angle choisi. Supposons que l'angle θ choisi soit situé à l'opposé du côté désigné c. En conséquence, nous obtenons le triangle ABD d'angle θ, qui est situé à l'opposé du côté un et les fêtes r. Le deuxième triangle est formé par l'angle θ, situé à l'opposé du côté b et les fêtes Avec longueur s, comme le montre la photo. Thabit Ibn Qurra a soutenu que les côtés de ces trois triangles sont liés comme suit :

À mesure que l'angle θ se rapproche de π/2, la base du triangle isocèle devient plus petite et les deux côtés r et s se chevauchent de moins en moins. Lorsque θ = π/2, ADB devient un triangle rectangle, r + s = c et nous obtenons le théorème initial de Pythagore.

Considérons l'un des arguments. Le triangle ABC a les mêmes angles que le triangle ABD, mais dans l'ordre inverse. (Les deux triangles ont un angle commun au sommet B, tous deux ont un angle θ et ont également le même troisième angle, basé sur la somme des angles du triangle.) En conséquence, ABC est similaire à la réflexion ABD du triangle DBA, comme montré dans la figure du bas. Écrivons la relation entre les côtés opposés et ceux adjacents à l'angle θ,

C'est aussi le reflet d'un autre triangle,

Multiplions les fractions et additionnons ces deux ratios :

Q.E.D.

Généralisation pour des triangles arbitraires via des parallélogrammes

Généralisation pour les triangles arbitraires,
zone verte parcelle = superficie bleu

Preuve de la thèse selon laquelle dans la figure ci-dessus

Faisons une généralisation supplémentaire pour les triangles non rectangles en utilisant des parallélogrammes sur trois côtés au lieu de carrés. (les carrés sont un cas particulier.) La figure du haut montre que pour un triangle aigu, l'aire du parallélogramme sur le côté long est égale à la somme des parallélogrammes des deux autres côtés, à condition que le parallélogramme sur le côté long Le côté est construit comme indiqué sur la figure (les dimensions indiquées par les flèches sont les mêmes et déterminent les côtés du parallélogramme inférieur). Ce remplacement des carrés par des parallélogrammes ressemble clairement au théorème initial de Pythagore, que l'on pense avoir été formulé par Pappus d'Alexandrie en 4 après JC. e.

La figure du bas montre la progression de la preuve. Regardons le côté gauche du triangle. Le parallélogramme vert gauche a la même aire que le côté gauche du parallélogramme bleu car ils ont la même base b et la hauteur h. De plus, le parallélogramme vert gauche a la même aire que le parallélogramme vert gauche dans l'image du haut car ils partagent une base commune (le côté supérieur gauche du triangle) et une hauteur commune perpendiculaire à ce côté du triangle. En utilisant un raisonnement similaire pour le côté droit du triangle, nous prouverons que le parallélogramme inférieur a la même aire que les deux parallélogrammes verts.

Nombres complexes

Le théorème de Pythagore est utilisé pour trouver la distance entre deux points dans un système de coordonnées cartésiennes, et ce théorème est valable pour toutes les coordonnées vraies : distance s entre deux points ( un B) Et ( CD) équivaut à

Il n'y a aucun problème avec la formule si les nombres complexes sont traités comme des vecteurs avec des composantes réelles X + je et = (X, oui). . Par exemple, la distance s entre 0 + 1 je et 1 + 0 je calculé comme le module du vecteur (0, 1) − (1, 0) = (−1, 1), ou

Cependant, pour les opérations avec des vecteurs aux coordonnées complexes, il est nécessaire d'apporter quelques améliorations à la formule de Pythagore. Distance entre les points avec des nombres complexes ( un, b) Et ( c, d); un, b, c, Et d tous complexes, nous les formulons en utilisant des valeurs absolues. Distance s basé sur la différence vectorielle (un − c, b − d) sous la forme suivante : laissez la différence un − c = p+je q, Où p- une vraie partie de la différence, q est la partie imaginaire, et je = √(−1). De même, laissez b − d = r+je s. Alors:

où est le nombre complexe conjugué de . Par exemple, la distance entre les points (un, b) = (0, 1) Et (c, d) = (je, 0) , calculons la différence (un − c, b − d) = (−je, 1) et le résultat serait 0 si des conjugués complexes n'étaient pas utilisés. Par conséquent, en utilisant la formule améliorée, nous obtenons

Le module est défini comme suit :

Stéréométrie

Une généralisation significative du théorème de Pythagore pour l'espace tridimensionnel est le théorème de Goy, du nom de J.-P. de Gois : si un tétraèdre a un angle droit (comme dans un cube), alors le carré de l'aire de la face opposée à l'angle droit est égal à la somme des carrés des aires des trois autres faces. Cette conclusion peut être résumée ainsi : « n-Théorème de Pythagore dimensionnel » :

Le théorème de Pythagore dans l'espace tridimensionnel relie la diagonale AD à trois côtés.

Autre généralisation : le théorème de Pythagore peut être appliqué à la stéréométrie sous la forme suivante. Considérons un parallélépipède rectangle comme indiqué sur la figure. Trouvons la longueur de la diagonale BD en utilisant le théorème de Pythagore :

où les trois côtés forment un triangle rectangle. On utilise la diagonale horizontale BD et l'arête verticale AB pour trouver la longueur de la diagonale AD, pour cela on utilise à nouveau le théorème de Pythagore :

ou, si nous écrivons tout dans une seule équation :

Ce résultat est une expression tridimensionnelle permettant de déterminer la norme du vecteur v(diagonale AD), exprimée en fonction de ses composantes perpendiculaires ( v k ) (trois côtés mutuellement perpendiculaires) :

Cette équation peut être considérée comme une généralisation du théorème de Pythagore pour l’espace multidimensionnel. Cependant, le résultat n’est en réalité rien d’autre qu’une application répétée du théorème de Pythagore à une séquence de triangles rectangles dans des plans successivement perpendiculaires.

Espace vectoriel

Dans le cas d'un système orthogonal de vecteurs, il existe une égalité, également appelée théorème de Pythagore :

Si - ce sont des projections du vecteur sur les axes de coordonnées, alors cette formule coïncide avec la distance euclidienne - et signifie que la longueur du vecteur est égale à la racine carrée de la somme des carrés de ses composantes.

L'analogue de cette égalité dans le cas d'un système infini de vecteurs est appelé égalité de Parseval.

Géométrie non euclidienne

Le théorème de Pythagore est dérivé des axiomes de la géométrie euclidienne et, en fait, n'est pas valable pour la géométrie non euclidienne, sous la forme sous laquelle il est écrit ci-dessus. (C’est-à-dire que le théorème de Pythagore s’avère être une sorte d’équivalent au postulat de parallélisme d’Euclide.) En d’autres termes, en géométrie non euclidienne, la relation entre les côtés d’un triangle sera nécessairement sous une forme différente du théorème de Pythagore. Par exemple, en géométrie sphérique, les trois côtés d'un triangle rectangle (disons un, b Et c), qui limitent l'octant (huitième partie) de la sphère unité, ont une longueur de π/2, ce qui contredit le théorème de Pythagore, car un 2 + b 2 ≠ c 2 .

Considérons ici deux cas de géométrie non euclidienne : géométrie sphérique et hyperbolique ; dans les deux cas, comme pour l'espace euclidien des triangles rectangles, le résultat, qui remplace le théorème de Pythagore, découle du théorème du cosinus.

Cependant, le théorème de Pythagore reste valable pour la géométrie hyperbolique et elliptique si l'exigence selon laquelle le triangle est rectangulaire est remplacée par la condition selon laquelle la somme des deux angles du triangle doit être égale au troisième, disons UN+B = C. Alors la relation entre les côtés ressemble à ceci : la somme des aires des cercles avec des diamètres un Et bégale à l'aire d'un cercle de diamètre c.

Géométrie sphérique

Pour tout triangle rectangle sur une sphère de rayon R.(par exemple, si l'angle γ dans un triangle est droit) avec des côtés un, b, c La relation entre les parties ressemblera à ceci :

Cette égalité peut être dérivée comme un cas particulier du théorème du cosinus sphérique, qui est valable pour tous les triangles sphériques :

où cosh est le cosinus hyperbolique. Cette formule est un cas particulier du théorème du cosinus hyperbolique, valable pour tous les triangles :

où γ est l'angle dont le sommet est opposé au côté c.

Où g je appelé tenseur métrique. Cela peut être fonction de la position. De tels espaces courbes incluent la géométrie riemannienne comme exemple général. Cette formulation convient également à l'espace euclidien lors de l'utilisation de coordonnées curvilignes. Par exemple, pour les coordonnées polaires :

Oeuvre vectorielle

Le théorème de Pythagore relie deux expressions de la grandeur d'un produit vectoriel. Une approche pour définir un produit vectoriel nécessite qu'il satisfasse à l'équation :

Cette formule utilise le produit scalaire. Le côté droit de l’équation est appelé déterminant de Gram pour un Et b, qui est égale à l'aire du parallélogramme formé par ces deux vecteurs. Sur la base de cette exigence, ainsi que de l'exigence selon laquelle le produit vectoriel est perpendiculaire à ses composantes un Et b il s'ensuit que, à l'exception des cas triviaux de l'espace à 0 et 1 dimension, le produit vectoriel n'est défini qu'en trois et sept dimensions. On utilise la définition de l'angle dans n-espace dimensionnel :

Cette propriété d’un produit vectoriel donne sa grandeur comme suit :

Grâce à l’identité trigonométrique fondamentale de Pythagore, nous obtenons une autre forme d’écriture de sa valeur :

Une approche alternative pour définir un produit vectoriel consiste à utiliser une expression pour son ampleur. Puis, en raisonnant dans l'ordre inverse, on obtient un lien avec le produit scalaire :

voir également

Remarques

1. Sujet d'histoire : le théorème de Pythagore dans les mathématiques babyloniennes
2. ( , p. 351) p. 351
3. ( , Vol I, p. 144)
4. Une discussion des faits historiques est donnée dans (, P. 351) P. 351
5. Kurt Von Fritz (avril 1945). « La découverte de l'incommensurabilité par Hippasus de Metapontum ». Les Annales des Mathématiques, Deuxième Série(Annales de mathématiques) 46 (2): 242–264.
6. Lewis Carroll, « L'histoire avec des nœuds », M., Mir, 1985, p. 7
7. Asger AaboeÉpisodes des débuts de l'histoire des mathématiques. - Association mathématique d'Amérique, 1997. - P. 51. - ISBN 0883856131
8. Proposition Python par Elisha Scott Loomis
9. d'Euclide Éléments: Livre VI, Proposition VI 31 : « Dans les triangles rectangles, la figure du côté sous-tendant l'angle droit est égale aux figures similaires et décrites de manière similaire sur les côtés contenant l'angle droit. »
10. Lawrence S.Leff travail cité. - Série éducative de Barron. - P. 326. - ISBN 0764128922
11. Howard Whitley Eves§4.8 :...généralisation du théorème de Pythagore // Grands moments des mathématiques (avant 1650). - Association mathématique d'Amérique, 1983. - P. 41. - ISBN 0883853108
12. Tâbit ibn Qorra (nom complet Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 après JC) était un médecin vivant à Bagdad qui a beaucoup écrit sur les éléments d'Euclide et d'autres sujets mathématiques.
13. Aydin Sayili (mars 1960). "Généralisation du théorème de Pythagore par Thâbit ibn Qurra." Isis 51 (1) : 35-37. est ce que je:10.1086/348837.
14. Judith D. Sally, Paul Sally Exercice 2.10 (ii) // Travaux cités. - P. 62. - ISBN 0821844032
15. Pour les détails d'une telle construction, voir George Jennings Figure 1.32 : Le théorème de Pythagore généralisé // Géométrie moderne avec applications : avec 150 figures. - 3ème. - Springer, 1997. - P. 23. - ISBN 038794222X
16. Arlen Brown, Carl M. Pearcy Article C: Norme pour un arbitraire n-tuple ... // Une introduction à l'analyse . - Springer, 1995. - P. 124. - ISBN 0387943692 Voir également pages 47 à 50.
17. Alfred Gray, Elsa Abbena, Simon Salamon Géométrie différentielle moderne des courbes et des surfaces avec Mathematica. - 3ème. - Presses CRC, 2006. - P. 194. - ISBN 1584884487
18. Rajendra Bhatia Analyse matricielle. - Springer, 1997. - P. 21. - ISBN 0387948465
19. Stephen W. Hawking travail cité. - 2005. - P. 4. - ISBN 0762419229

Théorème

Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des jambes (Fig. 1) :

$c^(2)=a^(2)+b^(2)$

Preuve du théorème de Pythagore

Soit le triangle $A B C$ un triangle rectangle d'angle droit $C$ (Fig. 2).

Traçons la hauteur du sommet $C$ à l'hypoténuse $A B$, et désignons la base de la hauteur par $H$.

Le triangle rectangle $A C H$ est similaire au triangle $A B C$ à deux angles ($\angle A C B=\angle C H A=90^(\circ)$, $\angle A$ est courant). De même, le triangle $C B H$ est similaire à $A B C$ .

En introduisant la notation

$$B C=a, A C=b, A B=c$$

de la similitude des triangles, nous obtenons que

$$\frac(a)(c)=\frac(H B)(a), \frac(b)(c)=\frac(A H)(b)$$

De là, nous avons ça

$$a^(2)=c \cdot H B, b^(2)=c \cdot A H$$

En additionnant les égalités résultantes, on obtient

$$a^(2)+b^(2)=c \cdot H B+c \cdot A H$$

$$a^(2)+b^(2)=c \cdot(H B+A H)$$

$$a^(2)+b^(2)=c \cdot A B$$

$$a^(2)+b^(2)=c \cdot c$$

$$a^(2)+b^(2)=c^(2)$$

Q.E.D.

Formulation géométrique du théorème de Pythagore

Théorème

Dans un triangle rectangle, l'aire du carré construit sur l'hypoténuse est égale à la somme des aires des carrés construits sur les pattes (Fig. 2) :

Exemples de résolution de problèmes

Exemple

Exercice.Étant donné un triangle rectangle $AB C$ dont les côtés mesurent 6 cm et 8 cm, trouvez l'hypoténuse de ce triangle.

Solution. D'après la condition de jambe $a=6$ cm, $b=8$ cm. Alors, d'après le théorème de Pythagore, le carré de l'hypoténuse

$c^(2)=a^(2)+b^(2)=6^(2)+8^(2)=36+64=100$

De là, nous obtenons que l'hypoténuse souhaitée

$c=\sqrt(100)=10$ (cm)

Répondre. 10 cm

Exemple

Exercice. Trouvez l'aire d'un triangle rectangle si l'on sait que l'une de ses pattes est 5 cm plus grande que l'autre et que l'hypoténuse mesure 25 cm.

Solution. Soit $x$ cm la longueur de la plus petite jambe, puis $(x+5)$ cm la longueur de la plus grande. Alors, d’après le théorème de Pythagore, on a :

$$x^(2)+(x+5)^(2)=25^(2)$$

Nous ouvrons les parenthèses, réduisons les parenthèses similaires et résolvons l'équation quadratique résultante :

$x^(2)+5x-300=0$

D'après le théorème de Vieta, on obtient que

$x_(1)=15$ (cm) , $x_(2)=-20$ (cm)

La valeur $x_(2)$ ne satisfait pas aux conditions du problème, ce qui signifie que la plus petite jambe mesure 15 cm et la plus grande jambe mesure 20 cm.

L'aire d'un triangle rectangle est égale à la moitié du produit des longueurs de ses pattes, soit

$$S=\frac(15 \cdot 20)(2)=15 \cdot 10=150\left(\mathrm(cm)^(2)\right)$$

Répondre.$S=150\gauche(\mathrm(cm)^(2)\droite)$

Référence historique

théorème de Pythagore- l'un des théorèmes fondamentaux de la géométrie euclidienne, établissant la relation entre les côtés d'un triangle rectangle.

L'ancien livre chinois "Zhou Bi Xuan Jing" parle d'un triangle de Pythagore ayant les côtés 3, 4 et 5. Le principal historien allemand des mathématiques, Moritz Cantor (1829 - 1920), estime que l'égalité $3^(2)+4^ (2)=5^ (2) $ était déjà connu des Égyptiens vers 2300 avant JC. Selon le scientifique, les constructeurs construisaient alors des angles droits en utilisant des triangles rectangles de côtés 3, 4 et 5. On en sait un peu plus sur le théorème de Pythagore chez les Babyloniens. Un texte donne un calcul approximatif de l'hypoténuse d'un triangle rectangle isocèle.

Actuellement, 367 preuves de ce théorème ont été enregistrées dans la littérature scientifique. Le théorème de Pythagore est probablement le seul théorème avec un nombre de preuves aussi impressionnant. Une telle diversité ne peut s’expliquer que par l’importance fondamentale du théorème pour la géométrie.

Le texte de l'ouvrage est affiché sans images ni formules.
La version complète de l'ouvrage est disponible dans l'onglet "Fichiers de travail" au format PDF

Introduction

Dans un cours de géométrie scolaire, seuls les problèmes mathématiques sont résolus à l'aide du théorème de Pythagore. Malheureusement, la question de l’application pratique du théorème de Pythagore n’est pas abordée.

À cet égard, le but de mon travail était de découvrir les domaines d'application du théorème de Pythagore.

Actuellement, il est généralement admis que le succès du développement de nombreux domaines scientifiques et technologiques dépend du développement de divers domaines des mathématiques. Une condition importante pour accroître l'efficacité de la production est l'introduction généralisée de méthodes mathématiques dans la technologie et l'économie nationale, ce qui implique la création de nouvelles méthodes efficaces de recherche qualitative et quantitative permettant de résoudre les problèmes posés par la pratique.

Je considérerai des exemples d'application pratique du théorème de Pythagore. Je n'essaierai pas de donner tous les exemples d'utilisation du théorème - cela serait difficilement possible. La portée du théorème est assez étendue et ne peut généralement pas être indiquée de manière suffisamment complète.

Hypothèse:

En utilisant le théorème de Pythagore, vous pouvez résoudre non seulement des problèmes mathématiques.

Pour ce travail de recherche, l’objectif suivant est défini :

Découvrez les domaines d'application du théorème de Pythagore.

Sur la base de l'objectif ci-dessus, les tâches suivantes ont été identifiées :

Recueillir des informations sur l'application pratique du théorème de Pythagore dans diverses sources et déterminer les domaines d'application du théorème.

Étudiez quelques informations historiques sur Pythagore et son théorème.

Montrez l'application du théorème à la résolution de problèmes historiques.

Traitez les données collectées sur le sujet.

J'étais engagé dans la recherche et la collecte d'informations - en étudiant des documents imprimés, en travaillant avec des documents sur Internet, en traitant les données collectées.

Méthodologie de recherche :

Étudier du matériel théorique.

Etude des méthodes de recherche.

Mise en œuvre pratique de l'étude.

Communicatif (méthode de mesure, questionnaire).

Type de projet: informations et recherches. Le travail a été effectué pendant le temps libre.

À propos de Pythagore.

Pythagore - philosophe grec ancien, mathématicien, astronome. Il a étayé de nombreuses propriétés des figures géométriques et développé une théorie mathématique des nombres et de leurs proportions. Il a apporté des contributions significatives au développement de l'astronomie et de l'acoustique. Auteur des Vers d'Or, fondateur de l'école pythagoricienne de Crotone.

Selon la légende, Pythagore serait né vers 580 avant JC. e. sur l'île de Samos dans une riche famille de marchands. Sa mère, Pyphasis, reçut son nom en l'honneur de Pythie, prêtresse d'Apollon. La Pythie a prédit à Mnésarque et à sa femme la naissance d'un fils, le fils porte également le nom de la Pythie. Selon de nombreux témoignages anciens, le garçon était fabuleusement beau et montra bientôt ses capacités extraordinaires. Il reçut ses premières connaissances de son père Mnesarchus, bijoutier et sculpteur de pierres précieuses, qui rêvait que son fils poursuive son activité. Mais la vie en a décidé autrement. Le futur philosophe a montré de grandes capacités pour la science. Parmi les professeurs de Pythagore se trouvaient Phérécyde de Syros et l'ancien Hermodamant. Le premier a inculqué au garçon l'amour de la science et le second - la musique, la peinture et la poésie. Par la suite, Pythagore rencontra le célèbre philosophe et mathématicien Thalès de Milet et, sur ses conseils, se rendit en Égypte, centre de l'activité scientifique et de recherche de l'époque. Après avoir vécu 22 ans en Égypte et 12 ans à Babylone, il retourne sur l'île de Samos, puis la quitte pour des raisons inconnues et s'installe dans la ville de Croton, dans le sud de l'Italie. Ici, il créa l'école (union) pythagoricienne, dans laquelle diverses questions de philosophie et de mathématiques étaient étudiées. À l'âge d'environ 60 ans, Pythagore épousa Théano, l'un de ses élèves. Ils ont trois enfants, qui deviennent tous des disciples de leur père. Les conditions historiques de cette époque sont caractérisées par un large mouvement du démos contre le pouvoir des aristocrates. Fuyant les vagues de colère populaire, Pythagore et ses étudiants s'installèrent dans la ville de Tarente. Selon une version : Kilon, un homme riche et méchant, est venu le voir, voulant rejoindre la confrérie alors qu'il était ivre. Ayant reçu un refus, Cylon commença à combattre Pythagore. Lors de l’incendie, les élèves ont sauvé la vie de l’enseignant à leurs propres dépens. Pythagore devint triste et se suicida bientôt.

Il convient de noter que c'est l'une des variantes de sa biographie. Les dates exactes de sa naissance et de son décès n'ont pas été établies, de nombreux faits sur sa vie sont contradictoires. Mais une chose est sûre : cet homme a vécu et a laissé à ses descendants un grand héritage philosophique et mathématique.

Théorème de Pythagore.

Le théorème de Pythagore est l’énoncé le plus important de la géométrie. Le théorème est formulé comme suit : l'aire d'un carré construit sur l'hypoténuse d'un triangle rectangle est égale à la somme des aires des carrés construits sur ses pattes.

La découverte de cette affirmation est attribuée à Pythagore de Samos (12ème siècle avant JC)

Une étude de tablettes cunéiformes babyloniennes et d'anciens manuscrits chinois (copies de manuscrits encore plus anciens) a montré que le célèbre théorème était connu bien avant Pythagore, peut-être plusieurs milliers d'années avant lui.

(Mais on suppose que Pythagore en a donné une preuve complète)

Mais il existe une autre opinion : dans l'école pythagoricienne, il y avait une merveilleuse coutume d'attribuer tous les mérites à Pythagore et de ne pas s'attribuer la gloire des découvreurs, sauf peut-être dans quelques cas.

(Écrivain de langue grecque Iamblique-Syrien, auteur du traité « La vie de Pythagore ». (IIe siècle après JC)

Ainsi, l'historien mathématique allemand Cantor estime que l'égalité 3 2 + 4 2 = 5 2 était

connu des Égyptiens vers 2300 avant JC. e. à l'époque du roi Amenehmet (d'après le papyrus 6619 du Musée de Berlin). Certains croient que Pythagore a donné au théorème une preuve complète, tandis que d'autres lui nient ce mérite.

Certains attribuent à Pythagore la preuve qu'Euclide en a donnée dans ses Éléments. D'autre part, Proclus (mathématicien, Ve siècle) affirme que la preuve dans les Éléments appartenait à Euclide lui-même, c'est-à-dire que l'histoire des mathématiques n'a conservé presque aucune donnée fiable sur l'activité mathématique de Pythagore. En mathématiques, il n’existe peut-être aucun autre théorème qui mérite toutes sortes de comparaisons.

Dans certaines listes des éléments d’Euclide, ce théorème était appelé « théorème de la nymphe » en raison de la similitude du dessin avec une abeille, un papillon (« théorème du papillon »), qui en grec était appelé une nymphe. Les Grecs utilisaient ce mot pour désigner d’autres déesses, ainsi que des jeunes femmes et des épouses. Le traducteur arabe n’a pas prêté attention au dessin et a traduit le mot « nymphe » par « mariée ». C’est ainsi qu’est apparu le nom affectueux de « théorème de la mariée ». Il existe une légende selon laquelle, lorsque Pythagore de Samos prouva son théorème, il remercia les dieux en sacrifiant 100 taureaux. D'où un autre nom - "le théorème des cent taureaux".

Dans les pays anglophones, on l'appelait : « moulin à vent », « queue de paon », « chaise de la mariée », « pont à âne » (si l'élève ne pouvait pas le « traverser », alors il était un véritable « âne »)

Dans la Russie pré-révolutionnaire, le dessin du théorème de Pythagore pour le cas d'un triangle isocèle était appelé « pantalon de Pythagore ».

Ces « pantalons » apparaissent lorsque vous construisez des carrés de chaque côté d’un triangle rectangle vers l’extérieur.

Combien de preuves différentes du théorème de Pythagore existe-t-il ?

Depuis l'époque de Pythagore, plus de 350 d'entre eux sont apparus et le théorème a été inclus dans le Livre Guinness des Records. Si l’on analyse les preuves du théorème, elles utilisent peu d’idées fondamentalement différentes.

Domaines d'application du théorème.

Il est largement utilisé pour résoudre géométrique Tâches.

C'est avec son aide que l'on peut trouver géométriquement les valeurs des racines carrées d'entiers :

Pour ce faire, nous construisons un triangle rectangle AOB (l'angle A est de 90°) avec des pattes unitaires. Alors son hypoténuse est √2. On construit ensuite un segment unitaire BC, BC est perpendiculaire à OB, la longueur de l'hypoténuse OC = √3, etc.

(on retrouve cette méthode chez Euclide et F. Kirensky).

Tâches en connaissance de cause physiciens Les lycées exigent la connaissance du théorème de Pythagore.

Ce sont des problèmes liés à l’addition de vitesses.

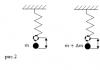
Faites attention à la diapositive : un problème tiré d'un manuel de physique de 9e année. D'un point de vue pratique, cela peut être formulé comme suit : sous quel angle par rapport au débit du fleuve un bateau transportant des passagers entre les quais doit-il se déplacer pour respecter l'horaire ? (les quais sont sur les rives opposées du fleuve)

Lorsqu’un biathlète tire sur une cible, il effectue un « ajustement au vent ». Si le vent souffle de la droite et que l’athlète tire droit, la balle ira vers la gauche. Pour atteindre la cible, vous devez déplacer le viseur vers la droite de la distance de déplacement de la balle. Des tableaux spéciaux ont été compilés pour eux (basés sur les corollaires de Pythagore). Le biathlète sait sous quel angle déplacer le viseur lorsque la vitesse du vent est connue.

Astronomie -également un large domaine d'application du théorème Trajet du faisceau lumineux. La figure montre le trajet d'un rayon lumineux provenant de UN vers B et retour. Le trajet du faisceau est représenté par une flèche incurvée pour plus de clarté ; en fait, le faisceau lumineux est droit.

Quel chemin prend le rayon ?? La lumière parcourt le même chemin d’avant en arrière. Quelle est la moitié de la distance parcourue par le rayon ? Si l'on désigne le segment UN B symbole je, la moitié du temps comme t, et désignant également la vitesse de la lumière avec la lettre c, alors notre équation prendra la forme

c * t = l

C'est le produit du temps passé et de la rapidité !

Essayons maintenant d'observer le même phénomène à partir d'un cadre de référence différent, par exemple, d'un vaisseau spatial volant devant un faisceau en mouvement à une vitesse v. Avec une telle observation, les vitesses de tous les corps changeront et les corps stationnaires commenceront à se déplacer à une vitesse v dans la direction opposée. Supposons que le navire se déplace vers la gauche. Ensuite, les deux points entre lesquels court le lapin commenceront à se déplacer vers la droite à la même vitesse. De plus, pendant que le lapin court son chemin, le point de départ UN se déplace et le faisceau revient à un nouveau point C.

Question : de combien de temps le point a-t-il le temps de se déplacer (de se transformer en point C) pendant le trajet du faisceau lumineux ? Plus précisément : quelle est la moitié de ce déplacement ? Si l'on note la moitié du temps de parcours du faisceau par la lettre t", et la moitié de la distance A.C. lettre d, alors on obtient notre équation sous la forme :

v * t" = ré

Lettre v indique la vitesse du vaisseau spatial.

Autre question : quelle distance parcourra le faisceau lumineux ?(Plus précisément, quelle est la moitié de ce chemin ? Quelle est la distance jusqu'à l'objet inconnu ?)

Si nous désignons la moitié de la longueur du trajet lumineux par la lettre s, nous obtenons l'équation :

c * t" = s

Ici c est la vitesse de la lumière, et t"- c'est la même heure que celle évoquée ci-dessus.

Considérons maintenant le triangle abc. C'est un triangle isocèle dont la hauteur est je, que nous avons introduit en considérant le processus d’un point de vue fixe. Puisque le mouvement est perpendiculaire je, alors cela ne pouvait pas l'affecter.

Triangle abc composé de deux moitiés - des triangles rectangles identiques dont les hypoténuses UN B Et AVANT JC. doit être relié aux jambes selon le théorème de Pythagore. L'une des jambes est d, que nous venons de calculer, et la deuxième branche est s, que traverse la lumière et que nous avons également calculée. Nous obtenons l'équation :

s 2 = je 2 +d 2

C'est théorème de Pythagore!

Phénomène aberration stellaire, découverte en 1729, est que toutes les étoiles de la sphère céleste décrivent des ellipses. Le demi-grand axe de ces ellipses est observé depuis la Terre sous un angle de 20,5 degrés. Cet angle est associé au mouvement de la Terre autour du Soleil à une vitesse de 29,8 km par heure. Pour observer une étoile depuis une Terre en mouvement, il est nécessaire d'incliner le tube du télescope vers l'avant en même temps que le mouvement de l'étoile, car pendant que la lumière parcourt la longueur du télescope, l'oculaire avance avec la terre. L'addition des vitesses de la lumière et de la Terre se fait de manière vectorielle, en utilisant ce qu'on appelle.

Pythagoras. U 2 =C 2 +V 2

Vitesse C de la lumière

Vitesse V-sol

Tube de télescope

À la fin du XIXe siècle, diverses hypothèses ont été faites sur l'existence d'habitants de Mars ressemblant à des humains, conséquence des découvertes de l'astronome italien Schiaparelli (il a découvert des canaux sur Mars qui ont longtemps été considérés comme artificiels). Naturellement, la question de savoir s’il est possible de communiquer avec ces créatures hypothétiques à l’aide de signaux lumineux a suscité de vives discussions. L'Académie des sciences de Paris a même institué un prix de 100 000 francs pour la première personne à établir un contact avec un habitant d'un autre corps céleste ; ce prix attend toujours l'heureux gagnant. Pour plaisanter, mais non sans raison, il a été décidé de transmettre un signal aux habitants de Mars sous la forme du théorème de Pythagore.

On ne sait pas comment procéder ; mais il est évident pour tout le monde que le fait mathématique exprimé par le théorème de Pythagore est valable partout, et donc les habitants d'un autre monde semblable au nôtre doivent comprendre un tel signal.

connexion mobile

Qui dans le monde moderne n’utilise pas de téléphone portable ? Chaque abonné de téléphonie mobile s'intéresse à sa qualité. Et la qualité, à son tour, dépend de la hauteur de l’antenne de l’opérateur mobile. Pour calculer le rayon dans lequel la transmission peut être reçue, nous utilisons théorème de Pythagore.

Quelle hauteur maximale doit avoir l'antenne d'un opérateur mobile pour que les émissions soient reçues dans un rayon de R=200 km ? (Le rayon de la Terre est de 6380 km.)

Solution:

Laisser AB = x , BC=R=200 km , OC= r =6380 km.

OB = OA + ABOB = r + x.

En utilisant le théorème de Pythagore, on obtient Réponse : 2,3 km.

Lors de la construction de maisons et de chalets, la question se pose souvent de la longueur des chevrons du toit si les poutres sont déjà réalisées. Par exemple : il est prévu de construire un toit à pignon sur une maison (forme en coupe). Quelle doit être la longueur des chevrons si les poutres sont réalisées AC=8 m et AB=BF.

Solution:

Le triangle ADC est isocèle AB=BC=4 m, BF=4 m. Si l'on suppose que FD=1,5 m, alors :

A) Du triangle DBC : DB=2,5 m.

B) Du triangle ABF :

Fenêtre

Dans les bâtiments Style gothique et roman les parties supérieures des fenêtres sont divisées par des nervures en pierre, qui non seulement jouent le rôle d'ornement, mais contribuent également à la solidité des fenêtres. La figure montre un exemple simple d'une telle fenêtre de style gothique. La méthode de construction est très simple : à partir de la figure, il est facile de trouver les centres de six arcs de cercle dont les rayons sont égaux.

largeur de fenêtre (b) pour arceaux extérieurs

la moitié de la largeur, (b/2) pour les arcs internes

Il reste un cercle complet touchant quatre arcs. Puisqu’il est enfermé entre deux cercles concentriques, son diamètre est égal à la distance entre ces cercles, soit b/2 et donc son rayon est b/4. Et puis ça devient clair et

la position de son centre.

DANS architecture romane Le motif représenté sur la figure est souvent retrouvé. Si b désigne toujours la largeur de la fenêtre, alors les rayons des demi-cercles seront R = b / 2 et r = b / 4. Le rayon p du cercle intérieur peut être calculé à partir du triangle rectangle illustré à la Fig. ligne pointillée L'hypoténuse de ce triangle, passant par le point de tangence des cercles, est égale à b/4+p, un côté est égal à b/4 et l'autre est b/2-p. D'après le théorème de Pythagore, on a :

(b/4+p) 2 =(b/4) 2 +(b/4-p) 2

b 2 /16+ pb/2+p 2 =b 2 /16+b 2 /4 - pb/2 +p 2 ,

En divisant par b et en ramenant des termes similaires, on obtient :

(3/2)p=b/4, p=b/6.

Dans l'industrie forestière: pour les besoins de la construction, les bûches sont découpées en poutres, et la tâche principale est d'obtenir le moins de déchets possible. La moindre quantité de déchets se produira lorsque le bois aura le plus grand volume. Que devrait contenir la section ? Comme le montre la solution, la section transversale doit être carrée et théorème de Pythagore et d'autres considérations nous permettent de tirer une telle conclusion.

Bois le plus volumineux

Tâche

À partir d'une bûche cylindrique, vous devez couper une poutre rectangulaire du plus grand volume. Quelle forme doit avoir sa section transversale (Fig. 23) ?

Solution

Si les côtés d'une section rectangulaire sont x et y, alors par le théorème de Pythagore

x 2 + y 2 = d 2,

où d est le diamètre de la bûche. Le volume d’une poutre est plus grand lorsque sa section transversale est la plus grande, c’est-à-dire lorsque xy atteint sa plus grande valeur. Mais si xy est le plus grand, alors le produit x 2 y 2 sera également le plus grand. Puisque la somme x 2 + y 2 est inchangée, alors, d'après ce qui a été prouvé précédemment, le produit x 2 y 2 est le plus grand lorsque

x 2 = y 2 ou x = y.

Ainsi, la section transversale de la poutre doit être carrée.

Tâches de transport(problèmes dits d'optimisation ; problèmes dont la solution nous permet de répondre à la question : comment allouer des fonds pour obtenir de grands avantages)

A première vue, rien de spécial : prendre des mesures de la hauteur du sol au plafond en plusieurs points, soustraire quelques centimètres pour que le meuble ne repose pas contre le plafond. Ce faisant, des difficultés peuvent survenir lors du processus d'assemblage des meubles. Après tout, les fabricants de meubles assemblent le cadre en plaçant le meuble en position horizontale, et lorsque le cadre est assemblé, ils le soulèvent en position verticale. Regardons la paroi latérale du meuble. La hauteur du meuble doit être inférieure de 10 cm à la distance du sol au plafond, à condition que cette distance ne dépasse pas 2 500 mm. Et la profondeur du meuble est de 700 mm. Pourquoi 10 cm, et non 5 cm ou 7, et qu'est-ce que le théorème de Pythagore a à voir là-dedans ?

Donc : paroi latérale 2500-100=2400 (mm) - hauteur maximale de la structure.

Pendant le processus de levage du cadre, la paroi latérale doit passer librement tant verticalement qu'en diagonale. Par théorème de Pythagore

AC = √ AB 2 + BC 2

CA = √ 2400 2 + 700 2 = 2500 (mm)

Que se passe-t-il si la hauteur du meuble est réduite de 50 mm ?

CA = √ 2450 2 + 700 2 = 2548 (mm)

Diagonale 2548 mm. Cela signifie que vous ne pouvez pas installer d’armoire (vous pourriez abîmer le plafond).

Paratonnerre.

On sait qu'un paratonnerre protège de la foudre tous les objets dont la distance à sa base n'excède pas le double de sa hauteur. Il est nécessaire de déterminer la position optimale du paratonnerre sur un toit à pignon, en garantissant sa hauteur accessible la plus basse.

D'après le théorème de Pythagore h 2 ≥une 2 +b 2 moyens h≥(une 2 +b 2) 1/2

Nous devons de toute urgence construire une serre pour les semis dans notre chalet d'été.

Un carré de 1 m 1 m est constitué de planches. Il y a des restes de film mesurant 1,5 m à 1,5 m. A quelle hauteur au centre du carré faut-il fixer la bande pour que le film la recouvre entièrement ?

1) Diagonale de serre d==1,4;0,7

2) Diagonale du film d 1= 2,12 1,06

3) Hauteur des rails x= 0,7

Conclusion

Grâce à mes recherches, j'ai découvert certains domaines d'application du théorème de Pythagore. J'ai collecté et traité de nombreux documents provenant de sources littéraires et d'Internet sur ce sujet. J'ai étudié quelques informations historiques sur Pythagore et son théorème. Oui, en effet, en utilisant le théorème de Pythagore, vous pouvez résoudre non seulement des problèmes mathématiques. Le théorème de Pythagore a trouvé son application dans la construction et l'architecture, les communications mobiles et la littérature.

Etude et analyse des sources d'information sur le théorème de Pythagore

ont montré que:

UN) l'attention exclusive des mathématiciens et des amateurs de mathématiques au théorème repose sur sa simplicité, sa beauté et sa signification ;

b) pendant de nombreux siècles, le théorème de Pythagore a été à l’origine de découvertes mathématiques intéressantes et importantes (théorème de Fermat, théorie de la relativité d’Einstein) ;

V) Théorème de Pythagore - est l'incarnation du langage universel des mathématiques, valable dans le monde entier ;

g) la portée du théorème est assez étendue et ne peut généralement pas être indiquée de manière suffisamment complète ;

d) les secrets du théorème de Pythagore continuent de passionner l'humanité et chacun de nous a donc la chance de participer à leur découverte.

Bibliographie

« Uspekhi Matematicheskikh Nauk », 1962, tome 17, n° 6 (108).

Alexander Danilovich Alexandrov (à l'occasion de son cinquantième anniversaire),

Alexandrov A.D., Werner A.L., Ryzhik V.I. Géométrie, 10 à 11 cellules. - M. : Éducation, 1992.

Atanasyan L.S. et autres Géométrie, 10 - 11 cellules. - M. : Éducation, 1992.

Vladimirov Yu.S. Espace - temps : dimensions explicites et cachées. - M. : « Sciences », 1989.

Volochine A.V. Pythagoras. - M. : Éducation, 1993.

Journal "Mathématiques", n°21, 2006.

Journal "Mathématiques", n°28, 1995.

Géométrie : Manuel. Pour les classes 7 à 11. collège/G.P. Bevz, V.G. Bevz, N.G. Vladimirova. - M. : Éducation, 1992.

Géométrie : manuel pour les niveaux 7 à 9. enseignement général Établissements/ L.S. Atanasyan, V.F. Butouzov, S.B. Kadomtsev et autres - 6e éd. - M. : Éducation, 1996.

Glazer G.I. Histoire des mathématiques à l'école : niveaux IX - X. Manuel pour les enseignants. - M. : Éducation, 1983.

Chapitres supplémentaires pour le manuel scolaire de 8e année : Manuel pour les élèves des écoles. et cours avancés étudié mathématiques / L.S. Atanasyan, V.F. Butouzov, S.B. Kadomtsev et autres - M. : Éducation, 1996.

Yelensky Shch. Sur les traces de Pythagore. M., 1961.

Kiselev A.P., Rybkin N.A. Géométrie : Planimétrie : 7e - 9e années : Manuel et cahier de problèmes. - M. : Outarde, 1995.

Klein M. Mathématiques. Recherche de la vérité : traduction de l’anglais. / Éd. et préface DANS ET. Archinova, Yu.V. Sachkova. - M. : Mir, 1998.

Liturman V. Théorème de Pythagore. - M., 1960.

Mathématiques : Manuel pour les écoliers et les étudiants / B. Frank et al. ; Traduction avec lui. - 3e éd., stéréotype. - M. : Outarde, 2003.

Peltuer A. Qui es-tu Pythagore ? - M. : Savoir, c'est pouvoir, n°12, 1994.

Perelman Ya. I. Mathématiques divertissantes. - M. : « Sciences », 1976.

Ponomareva T.D. De grands scientifiques. - M. : Maison d'édition Astrel LLC, 2002.

Sveshnikova A. Voyage dans l'histoire des mathématiques. - M., 1995.

Semenov E.E. Étudier la géométrie : Livre. Pour les élèves de la 6e à la 8e année. moyenne scolaire - M. : Éducation, 1987.

Smyshlyaev V.K. À propos des mathématiques et des mathématiciens. - Maison d'édition de livres Mari, 1977.

Tuchnine N.P. Comment poser une question. - M. : Éducation, 1993.

Cherkasov O.Yu. Planimétrie au concours d'entrée. - M. : Lycée de Moscou, 1996.

Dictionnaire encyclopédique d'un jeune mathématicien. Comp. A.P. Savine. - M. : Pédagogie, 1985.

Encyclopédie pour enfants. T. 11. Mathématiques. /Chapitre Éd. MARYLAND. Aksénov. - M. : Avanta+, 2001.